广东省汕头市潮南区陈店公校2024-2025学年七年级下学期期末数学试题
试卷更新日期:2025-07-07 类型:期末考试
一、选择题(本大题共 10小题,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列调查中,最适合采用全面调查(普查)方式的是( )A、调查全市中学生每天体育锻炼时间 B、调查某款新能源汽车的抗撞击能力 C、调查神舟十九号飞船各零件是否合格 D、调查全市中学生视力情况2. 在平面直角坐标系中,点 P 在第一象限,且到 x 轴距离为 2,到 y 轴距离为 4,则点 P 的坐标为( )A、(2,4) B、(4,2) C、(-2,-4) D、(-4,-2)3. 一个正方形的面积是8,估计它的边长大小在( )A、1与2之间 B、2与3之间 C、3与4之间 D、4与5之间4. 下列四个数 , , -0.2025,中,无理数的个数是( )A、0 个 B、1 个 C、2 个 D、3 个5. 已知是关于x,y的二元一次方程组的解,那么a,b的值分别为( )A、 , B、 , C、 , D、 ,6. 如图是篱笆围栏抽象出几何图形的一部分,则下列条件中能判断直线的是( )
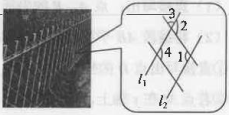 A、 B、 C、 D、7. 若 , 则下列不等式错误的是( )A、 B、 C、 D、8. 下列所示的四个图形中, 和 是同位角的是( )
A、 B、 C、 D、7. 若 , 则下列不等式错误的是( )A、 B、 C、 D、8. 下列所示的四个图形中, 和 是同位角的是( )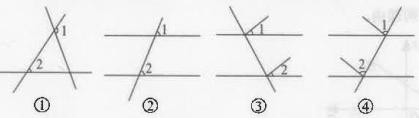 A、③ B、①②③ C、①②④ D、①④9. 如果关于 x 的不等式组 的解集是 , 则 a 的取值范围是 ( )A、 B、 C、 D、10. 若方程组的解是 , 则方程组的解是( )A、 B、 C、 D、
A、③ B、①②③ C、①②④ D、①④9. 如果关于 x 的不等式组 的解集是 , 则 a 的取值范围是 ( )A、 B、 C、 D、10. 若方程组的解是 , 则方程组的解是( )A、 B、 C、 D、二、填空题(本大题共5小题)
-
11. 在“Deep Seek”的所有字母中,字母“e”出现的频率为.12. 的平方根是 .13. 有下列命题:①两直线平行,同位角相等;②垂线段最短;③同角的余角相等;④同旁内角互补;⑤两点确定一条直线.其中假命题是(填序号).14. 已知 , 则的值为.15. 已知直线 轴,点M的坐标为(1,2),并且线段 , 则点N的坐.标为.
三、解答题(一)(本大题共3小题)
-
16. 计算:.17. 解不等式: , 并把它的解集表示在数轴上.
 18. 如图, , , .
18. 如图, , , .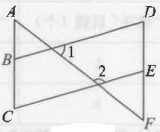 (1)、 求证:.(2)、 探索与的数量关系,并说明理由.
(1)、 求证:.(2)、 探索与的数量关系,并说明理由.四、解答题(二)(本大题共3小题)
-
19. 2025年中央电视台春节联欢晚会,作为春节申遗成功后的首届春晚,整场晚会以“已巳如意,生生不息”为主题,充分展示中华优秀传统文化的永水魅力. 为了解某校九年级学生观看春晚的方式(A. 平板观看;B. 手机观看;C. 电视观看;D. 其他方式或没有观看),小明随机统计了部分学生的春晚观看方式,并绘制成如下统计图:
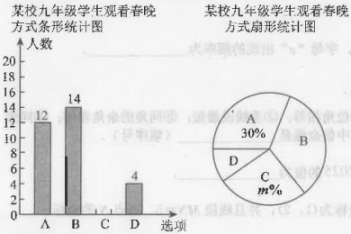
请根据图中信息解答下列问题:
(1)、 求这次随机抽取的学生人数,并将条形统计图补充完整;(2)、 扇形统计图中,m的值为 , “B.手机观看”所对应扇形的圆心角度数为;(3)、 该校九年级共有学生1000人,请估计九年级学生用电视观看春晚的学生约有多少人?20. 已知关于x,y的方程组.(1)、 方程的正整数解有:;(2)、 若方程组的解满足 , 求m的值;(3)、 若x,y满足 , 求m的取值范围.21. 电影《哪吒之魔童闹海》的热播,促进了文创市场的发展.经了解,某商店销售“哪吒”和“敖丙”两种文创玩偶的数量和金额如下:“哪吒”玩偶(个)
“敖丙”玩偶(个)
金额(元)
1
2
60
3
4
136
(1)、该商店和“敖丙”两种文创玩偶的销售单价分别是多少元/件?(2)、为庆祝“六一”儿童节,潘潘妈妈为班里的小朋友准备礼物.准备到该商店购买“哪吒”和“敖丙”两种文创玩偶共30件,其中“敖丙”玩偶的数量不少于“哪吒”玩偶的数量,且购买总费用不超过582元,有哪几种购买方案?哪种购买方案费用最少?五、解答题(三)(本大题共2小题)
-
22. 【概念学习】在平面直角坐标系中,对于P,Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P,Q两点为同距点. 如下图中的P(-2,3),Q(3,2)两点即为同距点.
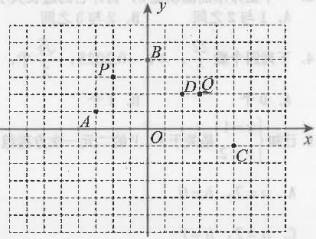 (1)、【理解概念】如图,写出点A,B,C,D的坐标: ( ▲ , ▲ ), ( ▲ , ▲ ), ( ▲ , ▲ ), ( ▲ , ▲ ),判断点B,C,D是否是点A的同距点;(2)、【深入探索】若点E(m-1,-1)是点A的同距点,求m的值;(3)、【拓展延伸】已知点N(-2,-1),若点F(a,b)为点N的同距点,且点F在第二象限,求出此时a,b之间的关系式.23. 如图,在平面直角坐标系中,点 , , 且 , m 是 64 的立方根.
(1)、【理解概念】如图,写出点A,B,C,D的坐标: ( ▲ , ▲ ), ( ▲ , ▲ ), ( ▲ , ▲ ), ( ▲ , ▲ ),判断点B,C,D是否是点A的同距点;(2)、【深入探索】若点E(m-1,-1)是点A的同距点,求m的值;(3)、【拓展延伸】已知点N(-2,-1),若点F(a,b)为点N的同距点,且点F在第二象限,求出此时a,b之间的关系式.23. 如图,在平面直角坐标系中,点 , , 且 , m 是 64 的立方根.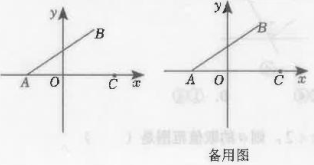 (1)、 直接写出:点 A,B 的坐标. ( , 0), ( , );(2)、 将线段 AB 平移得到线段 CD,点 B 的对应点是点 C(8,0),点 A 的对应点是点 D.
(1)、 直接写出:点 A,B 的坐标. ( , 0), ( , );(2)、 将线段 AB 平移得到线段 CD,点 B 的对应点是点 C(8,0),点 A 的对应点是点 D.① 直接写出点 D 的坐标:( ▲ , ▲ );
② 若点 M 在 y 轴上,且三角形 ACM 的面积是 6,求点 M 的坐标;
(3)、 在(2)的条件下,点 E 在 y 轴负半轴上运动,但不与点 D 重合,写出 、、 之间的数量关系,并说明理由.