3.1-2 确定位置与平面直角坐标系-北师大版(2025)数学八年级上册

试卷更新日期：2025-06-29 类型：同步测试

进入出卷网下载

一、选择题

1. 国庆假期，小磊和小强去电影院观看了首部聚焦“外交官撤侨”的电影《万里归途》，若电影票上小磊的座号“5排6座”记作 $(5 ， 6)$ ，则小强的座号“6排7座”可记作（）

A、 $(- 6 ， 7)$ B、 $(6 ， 7)$ C、 $(7 ， 6)$ D、 $(- 6 ， - 7)$

查看试题解析
2. 如图，雷达探测器测得六个目标A，B，C，D，E，F出现.按照规定的目标表示方法，目标C，F的位置分别表示为 $C (6 ， 12 0^{°}) ， F (5 ， 120 ° ）$ ，按照此方法表示目标A，B，D，E的位置，其中表示不正确的是（）

A、 $A (5 ， 3 0^{°})$ B、 $B (2 ， 9 0^{°})$ C、 $D (4 ， 24 0^{°})$ D、 $E (3 ， 6 0^{°})$

查看试题解析
3. 在平面直角坐标系中，点 $(1 ， - 2)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 在平面直角坐标系中，已知点 $P (- 5, m)$ 在第三象限，则 $m$ 的值可能为（）

A、 $- 1$ B、4 C、0 D、 $\frac{1}{3}$

查看试题解析
5. 在平面直角坐标系中，点 $M (m - 3 ， m + 1)$ 在 $x$ 轴上，则点 $M$ 的坐标为（）．

A、 $(- 4 ， 0)$ B、 $(0 ， - 2)$ C、 $(- 2 ， 0)$ D、 $(0 ， - 4)$

查看试题解析
6. 已知点P（1－2m，m－1），则不论m取什么值，该P点必不在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
7. 如图，一个点在第一象限及x轴.y轴上运动，且每秒移动一个单位，在第1秒钟，它从原点运动到（0，1），然后接着按图中箭头所示方向运动[即（0，0）→（0，1）→（1，1）→（1，0）→…]，那么第35秒时质点所在位置的坐标是（）

A、（4，0） B、（0，5） C、（5，0） D、（5，5）

查看试题解析
8. 若点M(x，y)坐标满足 $(x + y)^{2} = x^{2} + y^{2} - 2,$ 则点M所在的象限是( )

A、第一象限或第三象限 B、第二象限或第四象限 C、第二象限或第三象限 D、无法确定

查看试题解析
9. 在平面直角坐标系中，已知点 $A (1, 2)$ ， $B (4, 5)$ ， $C (5, 2)$ ，如果存在点 $E$ ，使 $△ A C E$ 和 $△ A C B$ 全等，则下列选项中不符合题意的点 $E$ 的坐标是（）

A、 $(2, 5)$ B、 $(3, 5)$ C、 $(4, - 1)$ D、 $(2, - 1)$

查看试题解析

二、填空题

10. 若某个电影院用 $(5 ， 12)$ 表示5排12号，则3排4号可以表示为．

查看试题解析
11. 已知点 $P (2 m + 1, m)$ 在 $y$ 轴上，则常数 $m =$

查看试题解析
12. 已知点P(a，b)， ab>0，a+b<0，则点 P在第象限.

查看试题解析
13. 直角坐标系中，点P（x，y）在第三象限，且P到x轴和y轴的距离分别为3，4，则点P的坐标为．

查看试题解析
14. 在平面直角坐标系中，点 $M (m + 3, 2 m + 4)$ 在 $y$ 轴上，则点 $M$ 的坐标是.

查看试题解析
15. 在平面直角坐标系中，第一象限内一点 $(m, 2 m - 1)$ 到x轴和y轴的距离相等，则 $m =$ ．

查看试题解析
16. 如图，平面上的25个点组成一个 $5 \times 5$ 的点阵，同一行或同一列中的两个相邻点之间的距离相等，在点阵中建立平面直角坐标系，若 $B (2, 0)$ ， $C (2, 4)$ ，则点 $A$ 的坐标为.

查看试题解析
17. 平面直角坐标系中有点 $A (0, 6)$ 、 $b (8, 0)$ ，连接 $A B$ ，以 $A B$ 为直角边在第一象限内作等腰直角三角形 $A B C$ ，则点C的坐标是.

查看试题解析

三、解答题

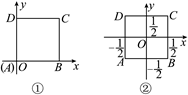
18. 已知点P（8﹣2m，m+1）．

(1)、若点P在y轴上，求m的值．

(2)、若点P在第一象限，且点P到x轴的距离是到y轴距离的2倍，求P点的坐标．

查看试题解析
19. 已知正方形ABCD的边长为1，分别写出图①和②中点A，B，C，D的坐标.

查看试题解析
20. 已知点A，B，C的坐标分别为(m，-2)，(3，m-1)，(2-n，3n+6).

(1)、若点C在y轴上，求n的值；

(2)、若AB所在的直线∥x轴，则AB的长为多少?

(3)、点C到两坐标轴的距离相等，求点C的坐标.

查看试题解析
21. 在平面直角坐标系中，给出如下定义：点P到x轴、y轴的距离的较大值称为点P的“长距”，点Q到x轴、y轴的距离相等时，称点Q为“角平分线点”．

(1)、点 $A (- 3, 5)$ 的“长距”为______；

(2)、若点 $B (4 - 2 a, - 2)$ 是“角平分线点”，求a的值；

(3)、若点 $C (- 2, 3 b - 2)$ 的长距为4，且点C在第二象限内，点D的坐标为 $(9 - 2 b, - 5)$ ，请判断点D是否为“角平分线点”，并说明理由．

查看试题解析
22. 如图，在直角梯形ABCD中，AD∥BC，AD=4，BC=6，AB=3.

(1)、建立适当的直角坐标系，并写出顶点A，B，C，D的坐标.

(2)、若要使点A的坐标为(-3，3)，该如何建立直角坐标系?

查看试题解析

四、实践探究题

23. 定义：在平面直角坐标系中，对于任意两点 $A (a ， b)$ ， $B (c ， d)$ ，若点 $T (x ， y)$ 满足 $x = \frac{a + c}{3}$ ， $y = \frac{b + d}{3}$ ，那么称点 $T$ 是点 $A$ 和 $B$ 的衍生点.例如： $M (- 2 ， 5)$ ， $N (8 ， - 2)$ ，则点 $T (2 ， 1)$ 是点 $M$ 和 $N$ 的衍生点.已知点 $D (3 ， 0)$ ，点 $E (m ， m + 2)$ ，点 $T (x ， y)$ 是点 $D$ 和 $E$ 的衍生点.

(1)、若点 $E (4 ， 6)$ ，则点 $T$ 的坐标为

(2)、请直接写出点 $T$ 的坐标（用 $m$ 表示）；

(3)、若直线 $E T$ 交 $x$ 轴于点 $H$ ，当 $∠ D H T = 90 °$ 时，求点 $E$ 的坐标.

查看试题解析
24. 我们在第十二章《全等三角形》中学习了全等三角形的性质和判定，在一些探究题中经常用以上知识转化角和边，进而解决问题．例如：我们在解决：“如图1，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，线段 $D E$ 经过点C，且 $A D ⊥ D E$ 于点D， $B E ⊥ D E$ 于点E．求证： $A D = C E$ ， $C D = B E$ ”这个问题时，只要证明 $△ A D C ≌ △ C E B$ ，即可得到解决，

(1)、积累经验：
请写出证明过程；

(2)、类比应用：
如图2，在平面直角坐标系中， $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，点A的坐标为 $(0 ， 2)$ ，点C的坐标为 $(1 ， 0)$ ，求点B与x轴的距离．

(3)、拓展提升：
如图3， $△ A B C$ 在平面直角坐标系中， $∠ A C B = 90 °$ ， $A C = B C$ ，点A的坐标为 $(2 ， 1)$ ，点C的坐标为 $(4 ， 2)$ ，求点B的坐标．

查看试题解析

五、阅读理解题

25. 已知当m ， n都是实数，且满足2m＝8+n时，称p（m﹣1， $\frac{n + 2}{2}$ ）为“开心点”．例如点A（5，3）为“开心点”．
∵当A（5，3）时，m﹣1＝5， $\frac{n + 2}{2}$ ＝3，得m＝6，n＝4，∴2m＝2×6＝12，
8+n＝8+4＝12，∴2m＝8+n ． ∴A（5，3）是“开心点”．

(1)、判断点B（9，6）是否为“开心点”，并说明理由；

(2)、若点M（a ， 2a-3）是“开心点”，请判断点M在第几象限？并说明理由．

查看试题解析