2.3.1二次根式(性质意义与乘除运算)-北师大版(2025)数学八年级上册
试卷更新日期:2025-06-28 类型:同步测试
一、选择题
-
1. 若式子在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、2. 函数的自变量的取值范围是( )A、 B、且 C、 D、且3. 若与最简二次根式是同类二次根式,则a的值为( )A、7 B、9 C、2 D、14. 若 ,则 的平方根为( )A、±2 B、4 C、2 D、±45. 当 , 时,在下列各式的计算中,正确的是( )A、 B、 C、 D、
二、填空题
-
6. 已知 , 化简: .7. 化简:= .8. 计算: .9. 计算 .10. 计算: = .11. 已知 , , 则.
三、计算题
-
12. 计算:13. 计算:14. 计算:15. 计算:
四、解答题
-
16. 已知 , 两数在数轴上的表示如图所示,化简: .
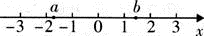 17. 阅读下面的解题过程体会如何发现隐含条件并回答下面的问题
17. 阅读下面的解题过程体会如何发现隐含条件并回答下面的问题化简: .
解:隐含条件 ,
解得 ,
∴ ,
∴原式
【启发应用】
(1)按照上面的解法,试化简(结果保留)
【类比迁移】
(2)实数a,b在数轴上的位置如图所示,化简:

(3)已知a,b,c为的三边长.化简:
18. 如图,实数在数轴上对应点的位置如图所示,化简的结果.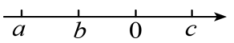 19. 已知成立。(1)、填空:的取值范围是.(2)、化简:20. 实数与满足.(1)、写出与的取值范围;(2)、已知是有理数,
19. 已知成立。(1)、填空:的取值范围是.(2)、化简:20. 实数与满足.(1)、写出与的取值范围;(2)、已知是有理数,①当是正整数时,求的值;
②当是整数时,若将符合条件的的值从大到小排列,求排在第3个位置和第11个位置的.
21. 我们规定用(a , b)表示一对数对,给出如下定义:记m= , n=(a>0,b>0),将(m , n)与(n , m)称为数对(a , b)的一对“对称数对”.例如(4,1)的一对“对称数对”为(2,1)与(1,2).(1)、数对(25,4)的一对“对称数对”是 和 ;(2)、若数对(x , 2)的一对“对称数对”的一个数对是( , 3),求x的值.五、实践探究题
-
22. 先来看一个有趣的现象: ,这里根号里 前后2经过适当的演变,竟“跑”到了根号外面,我们不妨把这种现象称为“穿墙”,具有这一性质的数还有许多,如 ,
(1)、猜想: = , 并验证你的猜想。
(2)、你能只用一个正数n(n≥2)来表示含有上述规律的等式吗?写出此等式,并证明。(3)、请再写出1个具有“穿墙”性质的数。23. 探究题:=3, =0.5, =6, = , =0.
根据以上算式,回答:
(1)、 一定等于a吗?如果不是,那么 =;(2)、利用你总结的规律,计算:①若x<2,则 =;
② = .
(3)、若a,b,c为三角形的三边长,化简: + + .