2.1 认识实数-北师大版(2025)数学八年级上册

试卷更新日期：2025-06-28 类型：同步测试

进入出卷网下载

一、选择题

1. 下列各数中， $3.14159 ， - \sqrt[3]{8} ， 0. 131131113 \cdot \cdot \cdot ， - π ， \sqrt{25} ， - \frac{1}{7}$ ，无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列说法正确的是（）

A、无限小数都是无理数 B、无理数包括正无理数、0、负无理数 C、带根号的数都是无理数 D、实数与数轴上的点是一一对应的

查看试题解析
3. 如图，数轴上的点 $C$ 表示的数是 $2$ ， $B C ⊥ O C$ 于点 $C$ ，且 $B C = 1$ ，连接 $O B$ ，以点 $O$ 为圆心， $O B$ 长为半径画弧与数轴交于点 $A$ ，则点 $A$ 表示的数是（）

A、 $\sqrt{5}$ B、 $- \sqrt{5}$ C、 $2 - \sqrt{5}$ D、 $\sqrt{5} - 2$

查看试题解析
4. 下列说法正确的个数为（　　）
①有理数与无理数的差都是有理数；②无限小数都是无理数；③无理数都是无限小数；④两个无理数的和不一定是无理数；⑤无理数分为正无理数、零、负无理数．

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 下列各组数中，互为相反数的是（）

A、 $- 2$ 与 $- \frac{1}{2}$ B、 $| - \sqrt{2} |$ 与 $\sqrt{2}$ C、 $\sqrt{{(- 2)}^{2}}$ 与 $\sqrt[3]{- 8}$ D、 $\sqrt[3]{- 8}$ 与 $- \sqrt[3]{8}$

查看试题解析
6. 若实数 $a$ 的立方根与 $b$ 的立方根互为相反数，则 $a$ 与 $b$ 的关系是（）

A、 $a = b = 0$ B、 $a = b$ C、 $a + b = 0$ D、 $a = \frac{1}{b}$

查看试题解析
7. 若 $\sqrt[3]{2 y - 1}$ 与 $\sqrt[3]{1 - 3 x}$ 互为相反数，则 $\frac{x}{y}$ 的值为（）．

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $- \frac{2}{3}$ D、 $- \frac{3}{2}$

查看试题解析
8. 数轴上表示 $1$ ， $\sqrt{2}$ 的对应点分别为 $A$ ， $B$ ，点 $B$ 关于点 $A$ 的对称点为 $C$ ，则点 $C$ 所表示的数是（）

A、 $\sqrt{2} - 1$ B、 $1 - \sqrt{2}$ C、 $2 - \sqrt{2}$ D、 $\sqrt{2} - 2$

查看试题解析

二、填空题

9. $π$ ， $\frac{22}{7}$ ， $\sqrt{8}$ ， $\sqrt[3]{343}$ ，3，1416， $\sqrt{3}$ 无理数的个数是个．

查看试题解析
10. $\sqrt{3}$ -2的相反数是，绝对值是

查看试题解析
11. 若无理数a满足：﹣4＜a＜﹣1，请写出两个你熟悉的无理数：

查看试题解析
12. 已知a ， b ， c是三角形的三边长，化简： $| a - b + c | - | a - b - c | =$ ．

查看试题解析
13. 点 $A$ 在数轴上表示的数是 $- \sqrt{15}$ ，点 $B$ 在数轴上表示的数为 $\sqrt{7}$ ，则A、B之间表示的整数点有个.

查看试题解析
14. 如下图，作一个以数轴的原点为圆心，长方形对角线为半径的圆弧，交数轴于点A，则点A表示的数是．

查看试题解析

三、解答题

15. 把下列各数分别填入相应的集合里．
﹣5，﹣2.626 626 662…，0，π，﹣ $\frac{7}{4}$ ，0.12，|﹣6|．
（1）正数集合：{                          …}；
（2）负数集合：{                          …}；
（3）有理数集合：{                          …}；
（4）无理数集合：{                          …}．

查看试题解析
16. 定义：可以表示为两个互质整数的商的形式的数称为有理数，整数可以看作分母为1的有理数；反之为无理数．如 $\sqrt{2}$ 不能表示为两个互质的整数的商，所以， $\sqrt{2}$ 是无理数．
可以这样证明：
设 $\sqrt{2} = \frac{a}{b}$ ， a与b 是互质的两个整数，且b≠0．
则 $2 = \frac{a^{2}}{b^{2}}$ a²=2b²因为b是整数且不为0，所以，a是不为0的偶数，设a=2n，（n是整数），所以b²=2n² ，所以b也是偶数，与a，b是互质的正整数矛盾．所以， $\sqrt{2}$ 是无理数．仔细阅读上文，然后，请证明： $\sqrt{5}$ 是无理数．

查看试题解析
17. 已知a ， b ， c是 $△ A B C$ 的三边长.

(1)、化简： $| a - b - c | + | b - c - a | + | b + c - a |$ ；

(2)、若 ${(2 a - b - 4)}^{2} + | a - 2 b + 7 | + {(c - 7)}^{2} = 0$ ，求 $△ A B C$ 的周长.

查看试题解析
18. 如图1，这是由8个同样大小的正方体组成的魔方，其体积为64．

(1)、求出这个魔方的棱长；

(2)、图1中阴影部分是一个正方形ABCD，求出阴影部分的边长及其面积；

(3)、如图2，把正方形ABCD放到数轴上，使点A与﹣1重合，那么点B表示的数为a，请计算（a﹣1）（a+1）﹣|2﹣a|的值．

查看试题解析

四、阅读理解题

19. 无限循环小数如何化为分数呢？请你仔细阅读下列资料：由于小数部分位数是无限的，所以不可能写成十分之几、百分之几、千分之几等等的数．转化时需要先去掉无限循环小数的“无限小数部分”．一般是用扩倍的方法，把无限循环小数扩大十倍、一百倍或一千倍…使扩大后的无限循环小数与原无限循环小数的“无限小数部分”完全相同，然后这两个数相减，这样“大尾巴”就剪掉了．例题：例如把 $0. \dot{3}$ 和 $0.2 \dot{1} \dot{7}$ 化为分数

请用以上方法解决下列问题

(1)、把 $0. \dot{1} \dot{7}$ 化为分数

(2)、把 $0.3 \dot{1} \dot{3}$ 化为分数．

查看试题解析
20. 阅读下列材料：“为什么 $\sqrt{2}$ 不是有理数”．
假 $\sqrt{2}$ 是有理数，那么存在两个互质的正整数m，n，使得 $\sqrt{2}$ = $\frac{n}{m}$ ，于是有2m²=n² ．
∵2m²是偶数，∴n²也是偶数，∴n是偶数．
设n=2t（t是正整数），则n²=2m，∴m也是偶数
∴m，n都是偶数，不互质，与假设矛盾．
∴假设错误
∵ $\sqrt{2}$ 不是有理数
有类似的方法，请证明 $\sqrt{3}$ 不是有理数．

查看试题解析

五、实践探究题

21. 勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一．它不但因证明方法层出不穷吸引着人们，更因为应用广泛而使人入迷．

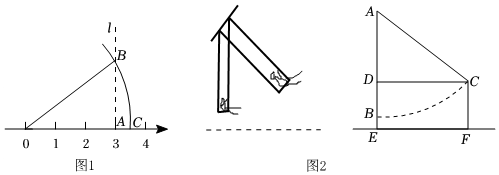(1)、应用场景 $1 — —$ 在数轴上画出表示无理数的点．
如图 $1$ ，在数轴上找出表示 $3$ 的点 $A$ ，过点 $A$ 作直线 $l$ 垂直于 $O A$ ，在 $l$ 上取点 $B$ ，使 $A B = 2$ ，以原点 $O$ 为圆心， $O B$ 为半径作弧，则弧与数轴的交点 $C$ 表示的数是．

(2)、应用场景 $2 — —$ 解决实际问题．
如图 $2$ ，秋千静止时，踏板离地的垂直高度 $B E = 1 m$ ，将它往前推 $6 m$ 至 $C$ 处时，水平距离 $C D = 6 m$ ，踏板离地的垂直高度 $C F = 4 m$ ，它的绳索始终拉直，求绳索 $A C$ 的长．

查看试题解析