平面几何的探究与压轴题型-2024-2025学年八年级下册北师大版数学
试卷更新日期:2025-06-13 类型:复习试卷
一、选择题
-
1. 如图所示,点A坐标为(-3,0) 点B坐标为(1,4),在y轴上存在一点C,使得△ABC为等腰三角形,则满足此条件的点C最多有( )
 A、4个 B、5个 C、6个 D、8个2. 如图,将矩形纸片沿对角线对折,使得点B落在点E处,交于点F,若平分 , , 则的长是( )
A、4个 B、5个 C、6个 D、8个2. 如图,将矩形纸片沿对角线对折,使得点B落在点E处,交于点F,若平分 , , 则的长是( ) A、1.5 B、 C、 D、3. 如图,矩形中, . 平分交于点 , 是上一动点,连结 , 于点 , 若 , 且 , 则的长为( )
A、1.5 B、 C、 D、3. 如图,矩形中, . 平分交于点 , 是上一动点,连结 , 于点 , 若 , 且 , 则的长为( ) A、 B、 C、 D、4. 已知P是等边三角形的边上的一点,若 , 则在以线段 , , 为边的三角形中,则最小内角的度数是( )
A、 B、 C、 D、4. 已知P是等边三角形的边上的一点,若 , 则在以线段 , , 为边的三角形中,则最小内角的度数是( ) A、 B、 C、 D、5. 如图,在中, , , O为的中点,将绕点O顺时针旋转得到 , D、E分别在边和的延长线上,连接 , 若 , 则的面积是( )
A、 B、 C、 D、5. 如图,在中, , , O为的中点,将绕点O顺时针旋转得到 , D、E分别在边和的延长线上,连接 , 若 , 则的面积是( ) A、 B、 C、 D、6. 如图,将两个全等的等腰直角三角形摆成如图所示的样子,其中 , , 、分别与交于D、E两点,将绕着点A顺时针旋转90°得到 , 则下列结论:①;②平分;③若 , 当时,则;④若平分 , 则 , 其中正确的个数有( )
A、 B、 C、 D、6. 如图,将两个全等的等腰直角三角形摆成如图所示的样子,其中 , , 、分别与交于D、E两点,将绕着点A顺时针旋转90°得到 , 则下列结论:①;②平分;③若 , 当时,则;④若平分 , 则 , 其中正确的个数有( ) A、1个 B、2个 C、3个 D、4个7. 如图,P是平分线上一点,OP=10, , 在绕点P旋转的过程中始终保持不变,其两边和OA,OB分别相交于M,N,下列结论:①是等边三角形;②MN的值不变;③OM+ON=10;④四边形PMON面积不变.其中正确结论的个数为( )
A、1个 B、2个 C、3个 D、4个7. 如图,P是平分线上一点,OP=10, , 在绕点P旋转的过程中始终保持不变,其两边和OA,OB分别相交于M,N,下列结论:①是等边三角形;②MN的值不变;③OM+ON=10;④四边形PMON面积不变.其中正确结论的个数为( ) A、4 B、3 C、2 D、18. 如图,在中,和的平分线相交于点 , 过点作分别交于点 . 喜欢探究的小东通过独立思考,得到以下结论:①当是的中点时;②当的形状变化时,点有可能为的中点.下列判断正确的是( )
A、4 B、3 C、2 D、18. 如图,在中,和的平分线相交于点 , 过点作分别交于点 . 喜欢探究的小东通过独立思考,得到以下结论:①当是的中点时;②当的形状变化时,点有可能为的中点.下列判断正确的是( ) A、①,②都正确 B、①,②都错误 C、①正确,②错误 D、①错误,②正确9. 在中, , , , 点N是边上一点.点M为边上的动点(不与点B重合),点D,E分别为 , 的中点,则的取值范围为( )
A、①,②都正确 B、①,②都错误 C、①正确,②错误 D、①错误,②正确9. 在中, , , , 点N是边上一点.点M为边上的动点(不与点B重合),点D,E分别为 , 的中点,则的取值范围为( ) A、 B、 C、 D、10. 如图,在中, , 若将该三角形往任意一方向一次性平移4个单位得到 , 分别取边的中点 , 则线段的长可能是( )
A、 B、 C、 D、10. 如图,在中, , 若将该三角形往任意一方向一次性平移4个单位得到 , 分别取边的中点 , 则线段的长可能是( ) A、6 B、7 C、2 D、3
A、6 B、7 C、2 D、3二、填空题
-
11. 在中, , , 有一个内角为 , 是直线上不同于点、的一点,且 , 则的长为 .12. 如图,在矩形中, , O为对角线的中点,点P在边上,且 , 点Q在边上,连接与 , 则的最大值为 , 的最小值为 .
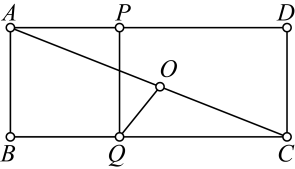 13. 已知,等边三角形 , 点D,E分别在边 , 上,且满足 , 连接 , , 交于点M.作 , 的角平分线,交于点N.连接 , 当时,的度数为 .
13. 已知,等边三角形 , 点D,E分别在边 , 上,且满足 , 连接 , , 交于点M.作 , 的角平分线,交于点N.连接 , 当时,的度数为 . 14. 如图,在平面直角坐标系中,是等边三角形,点 , 直线绕轴上一点顺时针旋转120°,得到的直线恰好经过点 , 则点的坐标是 .
14. 如图,在平面直角坐标系中,是等边三角形,点 , 直线绕轴上一点顺时针旋转120°,得到的直线恰好经过点 , 则点的坐标是 . 15. 旋转变换在几何证明或计算中有很重要的应用,利用旋转解决问题:如图,P为正方形 内一点, , , ,则 .
15. 旋转变换在几何证明或计算中有很重要的应用,利用旋转解决问题:如图,P为正方形 内一点, , , ,则 . 16. 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO' , 连接AO' . 则下列结论:
16. 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO' , 连接AO' . 则下列结论:
①△BO'A可以由△BOC绕点B逆时针方向旋转60°得到;
②连接OO' , 则OO'=4;
③∠AOB=150°;
④S四边形AOBO'=6+4 .
其中正确的结论是 .
17. 如图,在平行四边形中, , , 是边延长线上一点,连接 , 以为边作等边三角形 , 连接 , 则的最小值是 .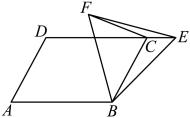 18. 如图,矩形中, , , 点G是边上的一点,点P是边上的一个动点,连接 , , 点E,F分别是 , 的中点,在点P的运动过程中,的最大长度为 .
18. 如图,矩形中, , , 点G是边上的一点,点P是边上的一个动点,连接 , , 点E,F分别是 , 的中点,在点P的运动过程中,的最大长度为 . 19. 如图, 在矩形 和矩形 中, 与 相交于点 与 相交于点 , 连接 , 并延长 与 相交于点 , 若 , 则下列结论正确的是。
19. 如图, 在矩形 和矩形 中, 与 相交于点 与 相交于点 , 连接 , 并延长 与 相交于点 , 若 , 则下列结论正确的是。① ;
②;
③ ;
④连接 , 若 , 四边形 与四边形 的面积之比为 .

三、实践探究题
-
20. 学习几何时,通常是先用几何的眼光去观察,再用代数的方法去验证网格是研究几何图形的一种工具,也是培养几何直观的一种方式.
 (1)、如图是正方形网格,正方形的顶点称为格点,每一个小正方形的边长为 .
(1)、如图是正方形网格,正方形的顶点称为格点,每一个小正方形的边长为 .
如图 , 点、在格点上,仅用无刻度的直尺找出线段的中点不写画法,保留画图痕迹;
如图 , 点、、在格点上,仅用无刻度的直尺找出的平分线交于点 , 并写出画图的步骤或依据;(2)、如图 , 在中, , , , 以为边在的左侧作等腰直角 , 连接 , 求的长.21.
(1)、【知识再现】如图1, 已知等腰中, , 平分 , D点在上.则与的位置关系是 , , 当 , 时, .(2)、【知识应用】如图2, 在中, , 平分交于E, , 且求的周长.(3)、【知识拓展】如图3,中, , , 是的角平分线,求的值.22. 综合与实践:【问题情境】
活动课上,同学们以等边三角形为背景开展旋转探究活动,数学小组经过研究发现“等边三角形在旋转过程中,对应边所在直线的夹角与旋转角存在一定关系”(注:平面内两直线的夹角是指两直线相交形成的小于或等于90°的角).如图1,将等边绕点A逆时针旋转15°得到 , 则线段与线段的夹角 . 如图2,将等边绕点A逆时针旋转100°得到 , 则线段与线段所在直线的夹角 .

【特例分析】
(1)如图1,若将等边绕点A逆时针旋转得到 , 线段与线段所在直线的夹角度数为______度;如图2,若将等边绕点A逆时针旋转得到 , 线段与线段所在直线的夹角度数为______度.
【类比分析】
(2)如图3,已知是等边三角形,分别在边和上截取和 , 使得 , 连接 . 如图4,将绕点A逆时针旋转(),连接 , 当和所在直线互相垂直时,线段之间有怎样的等量关系?试探究你的结论,并说明理由.
【延伸应用】
(3)在(2)的条件下,如图3,若 , , 将绕点A逆时针旋转().当和所在直线互相垂直时,请直接写出此时的长.
23. (1)、【案例展示】如图 , 点、分别在正方形的边、上, , 连接 , 则 , 理由如下:
(1)、【案例展示】如图 , 点、分别在正方形的边、上, , 连接 , 则 , 理由如下:
, 可把绕点逆时针旋转至 , 可使与重合,
,
, 点、、共线,由旋转得:≌ ,
, , , 而 ,
, 即 ,
≌ , 根据是第一空填三角形,第二空填全等的依据 ,
,
又 ,
.(2)、【类比引申】如图 , 四边形中, , 点、分别在边、上,若、都不是直角时仍成立,则与应该满足什么数量关系是 .(3)、【拓展运用】如图 , 在中, , , 点、均在边上,且猜想、、应满足的等量关系,并写出推理过程.24.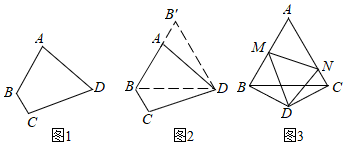
【问题提出】如图 , 在四边形中, , , , , , 求四边形的面积.
【尝试解决】旋转是一种重要的图形变换,当图形中有一组邻边相等时,往往可以通过旋转解决问题.
(1)、如图2,连接 , 由于 , 所以可将绕点顺时针方向旋转 , 得到 , 则的形状是 .(2)、在(1)的基础上,求四边形的面积.(3)、【类比应用】如图 , 等边的边长为 , 是顶角为的等腰三角形,以D为顶点作一个的角,角的两边分别交于点 , 交于点 , 连接 , 求的周长.
25. 【教材呈现】如图是华师版八年级下册数学教材第页的部分内容.平行四边形的性质定理平行四边形的对角线互相平分我们可以用演绎推理证明这个结论.
已知:如图 , ▱的对角线和相交于点 .
求证: , .
 (1)、请根据教材提示,结合图 , 写出完整的证明过程.(2)、【性质应用】如图 , 在▱中,对角线 , 相交于点 , 过点且与边 , 分别相交于点 , 求证: .(3)、【拓展提升】在【性质应用】的条件下,连接若 , 的周长是 , 则▱的周长是 .26. 综合与实践
(1)、请根据教材提示,结合图 , 写出完整的证明过程.(2)、【性质应用】如图 , 在▱中,对角线 , 相交于点 , 过点且与边 , 分别相交于点 , 求证: .(3)、【拓展提升】在【性质应用】的条件下,连接若 , 的周长是 , 则▱的周长是 .26. 综合与实践特例感知:
如图1,在等边三角形中,是延长线上一点,且 , 以为边作等边三角形 , 连接 , 分别过点作 , 过点作 , 交于点 , 连接与交于点 .


 (1)、试判断和的数量关系,并说明理由.(2)、猜想论证:将绕点按顺时针方向旋转一定角度得到图2,则(1)中和的数量关系是否仍然成立?请说明理由.(3)、拓展延伸:将如图1所示的绕点按逆时针方向旋转角度 , 当时,请直接写出的值.27. 综合与实践:折纸是一项有趣的活动,折纸活动也伴随着我们初中数学的学习.在折纸过程中,我们可以研究图形的运动和性质,也可以在思考问题的过程中,初步建立几何直观,现在就让我们带着数学的眼光来折纸吧.
(1)、试判断和的数量关系,并说明理由.(2)、猜想论证:将绕点按顺时针方向旋转一定角度得到图2,则(1)中和的数量关系是否仍然成立?请说明理由.(3)、拓展延伸:将如图1所示的绕点按逆时针方向旋转角度 , 当时,请直接写出的值.27. 综合与实践:折纸是一项有趣的活动,折纸活动也伴随着我们初中数学的学习.在折纸过程中,我们可以研究图形的运动和性质,也可以在思考问题的过程中,初步建立几何直观,现在就让我们带着数学的眼光来折纸吧.定义:将纸片折叠,若折叠后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为完美矩形.
 (1)、操作发现:
(1)、操作发现:如图①,将纸片按所示折叠成完美矩形 , 若的面积为24, , 则此完美矩形的边长 , 面积为 .
(2)、类比探究:如图②,将平行四边形纸片按所示折叠成完美矩形 , 若平行四边形的面积为 , , 则完美矩形的周长为 .
(3)、拓展延伸:如图③,将平行四边形纸片按所示折叠成完美矩形 , 若 , , 求此完美矩形的周长为多少.
28. 某数学兴趣小组对对角线互相垂直的四边形进行了探究,得出了如下结论:如图1,若四边形的对角线与相交于点 , 且 , 则四边形的四条边长满足 .
 (1)、简单应用:如图1,四边形中, , , , , 则边;(2)、发现应用:如图2,若 , 分别是中 , 边上的中线.且垂足为 , 求证:;(3)、拓展应用:如图3,中,点、、分别是 , , 的中点.若 , , . 求线段的长.
(1)、简单应用:如图1,四边形中, , , , , 则边;(2)、发现应用:如图2,若 , 分别是中 , 边上的中线.且垂足为 , 求证:;(3)、拓展应用:如图3,中,点、、分别是 , , 的中点.若 , , . 求线段的长.