【培优练】人教版数学八年级下学期 20.1.2 中位数和众数

试卷更新日期：2025-06-12 类型：同步测试

进入出卷网下载

一、选择题

1. 据统计，某班7个学习小组上周参加“青年大学习!的人数分别为：6，6，7，7，7，8，8，这组数据的中位数是（）

A、6 B、7 C、8 D、9

查看试题解析
2. 第8个全国近视防控宣传教育月的主题是“有效减少近视发生，共同守护光明未来”．某校积极响应，开展视力检查．某班51名同学视力检查数据如下表：
视力
4.3
4.4
4.5
4.6
4.7
4.8
4.9
5.0
人数
7
4
4
7
11
10
5
3
这51名同学视力检查数据的众数是（）.

A、4 B、4.7 C、7 D、4.6或4.3

查看试题解析
3. 已知一组数据：35，33，31，35，36，这组数据的平均数和中位数分别是（）

A、34，35 B、34，34 C、35，34 D、35，35

查看试题解析
4. 某校为了解学生的课外阅读情况，随机抽取了40名学生，对他们一周的课外阅读时间进行了统计，数据如下表，则这些学生一周课外阅读时间的中位数和众数分别是（）
读书时间
6小时及以下
7小时
8 小时
9小时
10小时及以上
学生人数
6
11
8
8
7

A、8，7 B、8，8 C、8.5，8 D、8.5，7

查看试题解析
5. 小明同学对数据26，36，36，46，5■，52进行统计分析．发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（）

A、平均数 B、方差 C、中位数 D、众数

查看试题解析
6. 一组数据按从小到大排列为3，4，7，x，15，17，若这组数据的中位数为9，则x是（）

A、9 B、10 C、11 D、12

查看试题解析
7. 在某一次数学测验中，随机抽取了10份试卷，其成绩如下：85、81、89、81、72、82、77、81、79、83则这组数据的众数、平均数与中位数分别为( )

A、81、82、81 B、81、81、76.5 C、83、81、77 D、81、81、81

查看试题解析
8. 已知一组数据 $3$ ， $a$ ， $4$ ， $6$ 的众数为 $3$ ，则这组数据的平均数为( )

A、 $3$ B、 $4$ C、 $5$ D、 $6$

查看试题解析
9. 某学校九年级一班十名同学定点投篮测试，每人投篮六次，投中的次数统计如下： $5$ ， $4$ ， $3$ ， $5$ ， $5$ ， $2$ ， $5$ ， $3$ ， $4$ ， $1$ ，则这组数据的中位数，众数分别为( )

A、 $4$ ， $5$ B、 $5$ ， $4$ C、 $4$ ， $4$ D、 $5$ ， $5$

查看试题解析
10. 在学校举办的“数学思维挑战赛”中，有19名选手进入决赛，将前9名晋级更高一级比赛，他们的决赛成绩各不相同，其中一名选手想知道自己是否晋级，除了知道自己的成绩外，他还需要了解这19名学生成绩的（　　）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析

二、填空题

11. 已知一组数据：4，5，a，6，7的平均数为6，则这组数据的中位数是.

查看试题解析
12. 某学校八年级有四个绿化小组，在植树节这天种下柏树的棵数如下：10，10，x，8.若这组数据的唯一众数和平均数相等，那么x=.

查看试题解析
13. 如表为某班某次心理测试成绩的统计表，已知全班共有38人且众数为50分，中位数为60分，则x²-y²的值等于
成绩（分)
20
30
40
50
60
70
90
100
次数（人)
2
3
5
x
6
y
3
4

查看试题解析
14. 已知数据a₁ ， a₂ ， a₃ ， a₄ ， a₅的平均数是m，且a₁＞a₂＞a₃＞a₄＞a₅＞0，则数据a₁ ， a₂ ， a₃ ， ﹣3，a₄ ， a₅的平均数和中位数分别是，．

查看试题解析
15. 若一组数据3，1，8，x ， 5的平均数为4，则这组数据的中位数为．

查看试题解析
16. 新星文学社40名学生中，13岁的有3人，14岁的有20人，15岁的有15人，16岁的有2人．该文学社学生年龄的平均数是，中位数是众数是.

查看试题解析
17. 已知一组数据：1，3，4，3，4．

(1)、这组数据的中位数为；

(2)、若添加数据3后组成新数据，则这组新数据的平均数（填“会”或“不会”）发生变化．

查看试题解析

三、解答题

18. 某公司有15名员工，他们所在部门及相应每人所创年利润如表所示．
部门
人数
每人所创年利润/万元
A
5
3
B
2
8
C
1
7
D
4
4
E
3
9

(1)、指出这个公司年利润的众数、中位数；

(2)、这个公司平均每人所创年利润是多少？

(3)、公司规定，个人所创年利润由高到低前40%的人可以获奖．试判断D部门的员工能否获奖，并说明理由．

查看试题解析
19. 2024 年 4 月 25 日 20 时 49 分，神舟十八号载人飞船发射成功，中国载人航天与空间站建设迎来全新的发展阶段．某中学为了解本校学生对我国航天科技及空间站的知晓情况，开展了 “航天梦科普知识” 竞赛活动，满分 10 分，学生得分均为整数．在初赛中，甲乙两组 (每组 10 人) 学生成绩如∶ (单位∶ 分)
甲组∶ $5 ， 6 ， 6 ， 6 ， 6 ， 6 ， 7 ， 7 ， 9 ， 10$ ．
乙组∶ $3 ， 6 ， 6 ， 6 ， 7 ， 7 ， 8 ， 8 ， 9 ， 9$ ．
组别
平均数
中位数
众数
甲组
$a$
$b$
6
乙组
6.9
7
$c$

(1)、以上成绩统计分析表中a= ， b= ， c= ；

(2)、小明同学说：“这次竞赛我得了 7 分，在我们小组中属中游偏上！ ” 观察上面表格判断，小明可能是组的学生．

查看试题解析
20. 为了增强学生的身体素质，助力学生全方位成长，某校积极组织了形式多样的课外体育活动．在九年级举办的篮球联赛进程中，甲、乙两位队员展现出了极为出色的表现，计分组在甲、乙两位队员最近的六场比赛里，得分、篮板以及失误这三个关键维度上的统计详情如下
队员
平均每场得分
得分中位数
平均每场篮板
平均每场失误
甲
m
27.5
8
2
乙
28
n
10
3
根据以上信息，回答下列问题．

(1)、表中的m＝，n＝；

(2)、请从得分方面分析：甲队员、乙队员在比赛中，（填“甲”或“乙”）队员表现更好；

(3)、规定“综合得分”为：平均每场得分×1+平均每场篮板×1.5+平均每场失误×（﹣1），且综合得分越高表现越好．请利用这种评价方法，比较哪位队员表现更好．

查看试题解析

四、实践探究题

21. “双碳”背景下，新能源汽车在主流的大众消费群体中越来越受欢迎

.

在会展中心举行一场新能源汽车车展活动中，共有三十几种不同品牌的新能源汽车参展，根据不同续航程将这些车分成六组，统计结果如下：

分组	$A$	$B$	$C$	$D$	$E$	$F$
$($ 单位：公里 $)$	$x \leq 400$	$400 < x \leq 500$	$500 < x \leq 600$	$600 < x \leq 700$	$700 < x \leq 800$	$x > 800$
数量 $($ 单位：辆 $)$	$40$	$120$	$132$	$95$	$68$	$45$

(1)、在参展的新能源汽车中，续航里程在组的车最多；续航里程的中位数落在组；

(2)、小渡家看中了售价一样的甲、乙两款汽车，根据汽车鉴定机构发布的数据对这两款车的续航里程、百公里加速、智能化水平三项性能进行了打分

(

百分制

)

，如下表：

	续航里程 $($ 分 $)$	百公里加速 $($ 分 $)$	智能化水平 $($ 分 $)$
甲车	$82$	$90$	$100$
乙车	$80$	$100$	$90$

小渡将续航里程、百公里加速、智能化水平三项性能的得分按 $5$ ： $2$ ： $3$ 的比例确定甲、乙两款汽车的最终得分，并以此为依据做出了选择，你知道小渡的选择是什么吗？请写出计算过程进行说明．

查看试题解析

五、阅读理解题

22. 甲、乙两支运动队各有10名队员，他们的年龄分布情况分别如图、表所示：

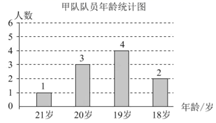
甲、乙两队队员年龄统计表

平均数（近似值）

众数

中位数

甲队

a

①

②

乙队

20

③

b

解决下列问题：

(1)、求甲队队员的平均年龄a的值．（结果取整数）

(2)、补全统计表中的①②③三处．

(3)、阅读理解-----扇形图中求中位数的方法．
[阅读与思考]

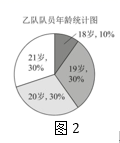
小明同学在求乙队队员年龄的中位数b时，是这样思考的：因为中位数是将一组数据按大小排序后，排在中间位置的一个数或中间两个数的平均数，那就需要先找到数据按大小排序后，大致排在50%附近的数，再根据中位数的概念进行细化求解．

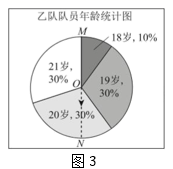
图2这个扇形图中的数据18~21是按大小顺序旋转排列的，我们就可以像图3所示的这样，先找到最大数据“21”与最小数据“18”的分界半径OM，为找到排在50%附近的数，再作出直径MN，那么射线ON指向的数据就是中位数．

王老师的评价：小明的这个方法是从中位数的概念出发，充分利用了扇形图的特性形象直观地解决问题．

[理解与应用]

请你利用小明的方法直接写出统计表中b的值．

查看试题解析

读书时间	6小时及以下	7小时	8 小时	9小时	10小时及以上
学生人数	6	11	8	8	7

队员	平均每场得分	得分中位数	平均每场篮板	平均每场失误
甲	m	27.5	8	2
乙	28	n	10	3

	平均数（近似值）	众数	中位数
甲队	a	①	②
乙队	20	③	b

视力	4.3	4.4	4.5	4.6	4.7	4.8	4.9	5.0
人数	7	4	4	7	11	10	5	3

成绩（分)	20	30	40	50	60	70	90	100
次数（人)	2	3	5	x	6	y	3	4

部门	人数	每人所创年利润/万元
A	5	3
B	2	8
C	1	7
D	4	4
E	3	9

组别	平均数	中位数	众数
甲组	$a$	$b$	6
乙组	6.9	7	$c$