【培优练】人教版数学八年级下学期 19.3 一次函数的应用与选择方案

试卷更新日期：2025-06-11 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，欣欣妈妈在超市购买某种水果所付金额y（元）与购买x（千克）之间的关系如图所示，则“一次性购买6千克这种水果”比“分2次每次购买3千克这种水果”可节省（）元．

A、4 B、3 C、2 D、1

查看试题解析
2. 小亮从家步行到公交车站台，等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法不正确的是（）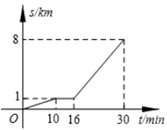

A、他离家8km共用了30min B、他等公交车时间为6min C、他步行的速度是100m/min D、公交车的速度是350m/min

查看试题解析
3. 小明同学在一次学科综合实践活动中发现，某品牌鞋子的长度y cm与鞋子的码数x之间满足一次函数关系，下表给出y与x的一些对应值：
码数x
26
30
34
42
长度y cm
18
20
22
26
根据小明的数据，可以得出该品牌38码鞋子的长度为（）

A、24cm B、25cm C、26cm D、38cm

查看试题解析
4. 向最大容量为60升的热水器内注水，每分钟注水10升，注水2分钟后停止1分钟，然后继续注水，直至注满.则能反映注水量与注水时间函数关系的图象是（）

A、 B、 C、 D、

查看试题解析
5. 声音在空气中传播的速度v（简称声速）与空气温度t的关系（如下表所示），则下列说法错误的是（    ）
温度 $t / ℃$
          $- 15$
          $- 10$
5
10
15
声速 $v / m / s$
321
324
333
336
339

A、在一定范围内，空气温度越高声速越快 B、空气温度每升高 $10 ℃$ ，声速增加 $6 m / s$ C、声速v与温度t之间的关系式为 $v = \frac{3}{5} t + 330$ D、当空气温度为 $20 ℃$ 时，声音 $5 s$ 可以传播 $1740 m$

查看试题解析
6. A、B两地相距12km，甲骑自行车从A地出发前往B地，同时乙步行从B地出发前往A地，如图所示的折线 $O - P - Q$ 和线段EF分别表示甲、乙两人与A地的距离y（km）与时间x（h）之间的函数关系，且OP与EF交于点G．下列说法中错误的是（）

A、甲乙出发后0.5h相遇 B、甲骑自行车的速度为 $18 k m / h$ C、两人相遇地点与A地的距离为9km D、甲、乙相距3km时，出发时间为 $x = \frac{3}{5} h$

查看试题解析
7. 在密码学中、直接可以看到的内容称为明码，对明码进行某种处理后得到的内容称为密码．有一种密码，将英文26个字母a，b，c，…，z（不分大小写）依次对应1，2，3，…，26这26个自然数（见表格）．当明码对应的序号x为奇数时，密码对应的序号 $y = \frac{x + 3}{2}$ ；当明码对应的序号x为偶数时，密码对应的序号 $y = \frac{x}{2} + 13$ ．按上述规定，明码和密码相同的序号为（）
字母
a
b
c
d
e
f
g
h
i
j
k
l
m
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
字母
n
o
p
q
r
s
t
u
v
w
x
y
z
序号
14
15
16
17
18
19
20
21
22
23
24
25
26

A、3 B、26 C、3和26 D、1和26

查看试题解析
8. 在物理实验课上，小鹏利用滑轮组及相关器材进行实验，他把得到的拉力 $F (N)$ 和所悬挂物体的重力 $G (N)$ 的几组数据用电脑绘制成如下图象（不计绳重和摩擦），请你根据图象判断以下结论正确的序号有（）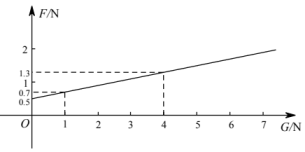
①物体的拉力随着重力的增加而增大；②当物体的重力 $G = 7$ N时，拉力 $F = 2.2$ N；③拉力F与重力G成正比例函数关系；④当滑轮组不悬挂物体时，所用拉力为0.5N．

A、①② B、②④ C、①④ D、③④

查看试题解析

9. 一家游泳馆的游泳收费标准为30元/次，若购买会员年卡，可享受如下优惠：

会员年卡类型	办卡费用/元	每次游泳收费/元
A类	50	25
B类	200	20
C类	400	15

例如，购买A类会员年卡，一年内游泳20次，消费50+25×20=550(元)，若一年内在该游泳馆游泳的次数介于45~55次之间，则最省钱的方式为（）

A、购买A类会员年卡 B、购买B类会员年卡 C、购买C类会员年卡 D、不购买会员年卡

查看试题解析

10. 张师傅驾车从甲地到乙地，两地相距 500 千米，汽车出发前油箱有油 25 升，途中加油若干升，加油前、后汽车都以 100 千米/时的速度匀速行驶，已知油箱中剩余油量 y（升）与行驶时间 t（小时）之间的关系如图所示．以下说法正确的有（）个
①加油前油箱中剩余油量 y（升）与行驶时间 t（小时）的函数关系是 y=－8t＋25
②汽车加油后还可行驶 4 小时
③途中加油 21 升
④汽车到达乙地时油箱中还余油 6 升

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 王刚同学步行从家里到距他家2000米的体育场参加活动，如果他步行的速度是每秒2.5米，那么王刚同学距体育场的路程y（米）与行走时间x（秒）的函数关系式为.

查看试题解析
12. 如图是某工程队在“村村通”工程中，修筑的公路长度y（米）与时间x（天）之间的关系图象．根据图象提供的信息，可知该公路的长度是米．

查看试题解析
13. 在测量某种液体密度的实验中，根据测得的该种液体和烧杯的总质量m（g）与该种液体的体积 $V (c m^{3})$ ，绘制了如图所示的函数图象（图中为一线段），则72g该种液体的体积为 $c m^{3}$ ．

查看试题解析
14. 在一条公路上每隔100千米有一个仓库（如图），共有4个仓库．A仓库存有15吨货物，B仓库存有20吨货物，D仓库存有30吨货物，C仓库是空的．现在想把所有的货物集中存放在一个仓库里，如果每吨货物运输1千米需要0.5元的运费，那么最少要花元运费才行．

查看试题解析
15. 数学学习小组准备利用一根弹簧制作一个简易弹簧秤 (用于称物体的质量)，需在刻度盘上标注刻度。经过四次试验与测量，得到弹簧的长度 $(c m)$ 与所挂物体的质量 $(k g)$ 之间的对应关系如下表：
物体的质量 $/ k g$
1
2
3
4
弹簧的长度 $/ c m$
10
12
14
16
已知该弹簧在挂物体后，在弹性限度内能达到的最大长度为 28 cm ，则学习小组在刻度盘上需标注的最大量程是kg 。

查看试题解析
16. 小明租用共享单车从家出发，匀速骑行到相距2400米的图书馆还书．小明出发的同时，他的爸爸以每分钟96米的速度从图书馆沿同一条道路步行回家，小明在图书馆停留了3分钟后沿原路按原速骑车返回．设他们出发后经过t（分）时，小明与家之间的距离为 $s_{1}$ （米），小明爸爸与家之间的距离为 $s_{2}$ （米），图中折线OABD、线段EF分别表示 $s_{1}$ 、 $s_{2}$ 与t之间的函数关系的图象．小明从家出发，经过分钟在返回途中追上爸爸．

查看试题解析
17. 甲，乙两车分别从A，B两地同时出发，以各自的速度匀速相向而行.当甲车到达B地后，发现有重要物品需要送给乙车，于是甲车司机立即通知乙车 $($ 通知时间忽略不计 $)$ ，乙车接到通知后将速度降 $50 %$ 继续匀速行驶，甲车司机花一定的时间准备好相关物品后，以原速的 $\frac{4}{3}$ 倍匀速前去追赶乙车，当甲车追上乙车时，乙车恰好到达A地.如图反映的是两车之间的距离 $y ($ 千米 $)$ 与乙车行驶时间 $x ($ 小时 $)$ 之同的函数关系，则甲车在B地准备好相关物品共花了小时.

查看试题解析
18. 某公司以A、B两种材料，利用不同的搭配方式推出了两款产品，其中，甲产品每份含200克A、200克B；乙产品每份含200克A、100克B，甲乙两种产品每份成本价分别为A、B两种材料的成本之和，若甲产品每份成本为16元，公司在核算成本的时候把A、B两种材料单价看反了，实际成本比核算时的成本多760元，如果每天甲销量的4倍和乙销量的3倍之和不超过120份，那么公司每天的实际成本最多为元.

查看试题解析

三、解答题

19. “十一”期间，小华一家人开车到距家100千米的景点旅游，出发前，汽车油箱内储油45升，当行驶60千米时，发现油箱余油量为31.5升（假设行驶过程中汽车的耗油量是均匀的）.

(1)、该车平均每千米的耗油量为升/千米；

(2)、写出余油量Q（升）与行驶路程x（千米）之间的关系式；

(3)、当油箱中余油量低于3升时，汽车将自动报警，若往返途中不加油，他们能否在汽车报警前回到家？说明理由.

查看试题解析
20. 科学家实验发现，声音在空气中的传播速度随温度的变化而变化，且满足某种函数关系.某兴趣小组为探究空气的温度 $x (℃)$ 与声音在空气中的传播速度y(米/秒)之间的关系，在标准实验室里进行了多次实验.下表为实验时记录的一些数据.
温度 $x (℃)$
…
0
5
10
15
20
…
声音在空气中的传播速度y(米 $/$ 秒)
…
331
334
337
340
343
…

(1)、如图，在给出的平面直角坐标系中，描出上面数据所对应的点.

(2)、根据描点发现，这些点大致位于同一个函数的图象上，则这个函数的类型最有可能是_▲_(填“一次函数”或“正比例函数”)，并求出该函数的解析式.

(3)、某地冬季的室外温度是 $- 10 ℃$ ，小明同学看到烟花3秒后才听到声响，利用第(2)问的函数，求小明与燃放烟花地的距离.(光的传播时间忽略不计)

查看试题解析
21. 如图，把一些相同规格的碗整齐地叠放在水平桌面上，这摞碗的高度随着碗的数量变化而变化的情况如表格所示：
碗的数量（只）
1
2
3
4
5
…
高度（cm）
4
5.2
6.4
7.6
8.8
…

(1)、h（cm）表示这摞碗的高度，x（只）表示这摞碗的数量，请用含x的代数式表示h；

(2)、若这摞碗共有15个，求这摞碗的高度；

(3)、若这摞碗的高度为11.2cm，求这摞碗的数量．

查看试题解析
22. 暑假期间，两名家长计划带领若干名学生去旅游，他们联系了报价均为每人1000元的两家旅行社，经协商，甲旅行社的优惠条件是：两名家长全额收费，学生都按七折收费；乙旅行社的优惠条件是家长、学生都按八折收费．假设这两位家长带领x名学生去旅游，他们应该选择哪家旅行社？

查看试题解析
23. 某商场计划从厂家购进 $A$ 、 $B$ 两款衣服共100件，这两款衣服的进价和售价如下表．设购进 $A$ 款衣服 $x$ 件，商场总利润为 $y$ 元．
品名
$A$
$B$
进价（元/件）
90
75
售价（元/件）
120
100

(1)、求 $y$ 关于 $x$ 的函数关系式；

(2)、厂家规定 $A$ 的进货数量不得超过 $B$ 进货数量的两倍，问应如何设计进货方案才能获得最大利润并求出最大利润；

(3)、为进一步激励销人员，商场准备实施奖励计划，每卖出一件 $A$ 衣服奖励 $m$ 元，每卖一件 $B$ 衣服奖励 $n$ 元，结果发现：若100件衣服均按原定售价卖完，无论购进 $A$ 商品多少件，商场利润恒为2000元，求 $m$ 、 $n$ 的值．

查看试题解析

四、实践探究题

24. 综合与实践

生活中的数学：如何确定单肩包最佳背带长度

素材1

如图是一款单肩包，背带由双层部分、单层部分和调节扣构成．使用时可以通过调节扣加长或缩短单层部分的长度，使背带的总长度加长或缩短（总长度为单层部分与双层部分的长度和，其中调节扣的长度忽略不计）

素材2

对该背包的背带长度进行测量，该双层的部分长度是 $x c m$ ，单层部分的长度是 $y c m$ ，得到如下数据：

双层部分长度 $x (c m)$	2	6	10
单层部分长度 $y (c m)$	116	108	100

素材3

单肩背包的最佳背带总长度与身高比例为 $2 : 3$

根据上述的素材，解决以下问题：

(1)、在下图的平面直角坐标系中，以表格中的x的值为横坐标，以y的值为纵坐标，描出所表示的点，并将这些点依次连接起来，观察这些点是否在同一条直线上，如果在同一条直线上，求出这条直线对应的函数解析式，如果不在同一直线上，请说明理由．

(2)、设人身高为h ，当单肩包背带长度调整为最佳背带总长度时，求此时人身高h与这款背包的背带双层部分的长度x之间的函数表达式．

(3)、身高

174 c m

的小明爸爸准备购买此款背包，爸爸自然站立，将该背包的背带调节到最短提在手上，当小明爸爸的单肩包背带长度调整为最佳背带总长度时．求此时双层部分的长度．

查看试题解析

温度 $t / ℃$	$- 15$	$- 10$	5	10	15
声速 $v / m / s$	321	324	333	336	339

字母	a	b	c	d	e	f	g	h	i	j	k	l	m
序号	1	2	3	4	5	6	7	8	9	10	11	12	13
字母	n	o	p	q	r	s	t	u	v	w	x	y	z
序号	14	15	16	17	18	19	20	21	22	23	24	25	26

温度 $x (℃)$	…	0	5	10	15	20	…
声音在空气中的传播速度y(米 $/$ 秒)	…	331	334	337	340	343	…

品名	$A$	$B$
进价（元/件）	90	75
售价（元/件）	120	100

码数x	26	30	34	42
长度y cm	18	20	22	26

物体的质量 $/ k g$	1	2	3	4
弹簧的长度 $/ c m$	10	12	14	16

碗的数量（只）	1	2	3	4	5	…
高度（cm）	4	5.2	6.4	7.6	8.8	…