【基础练】人教版数学八年级下学期 19.3 一次函数的应用与选择方案

试卷更新日期：2025-06-11 类型：同步测试

进入出卷网下载

一、选择题

1. 某汽车油箱中盛有油 $100 L$ ，装满货物行驶的过程中每小时耗油8L，则油箱中的剩油量 $Q (L)$ 与时间 $t (h)$ 之间的关系式是（）

A、 $Q = 100 + 8 t$ B、 $Q = 8 t$ C、 $Q = 100 - 8 t$ D、 $Q = 8 t - 100$

查看试题解析
2. 某生物小组观察一植物生长，得到的植物高度y(单位：厘米)与观察时间x(单位：天)的关系，并画出如下图所示的图象(AC是线段，直线CD平行于x轴)．下列说法错误的是（）

A、从开始观察时起，50天后该植物停止长高 B、直线AC的函数表达式为 $y = \frac{1}{5} x + 6$ C、第40天，该植物的高度为14厘米 D、该植物最高为15厘米

查看试题解析
3. 某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分，乙厂直接按印刷数量收取印刷费．甲、乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图分别如图中甲、乙所示，有下列三种说法：
①甲厂的制版费为1千元；
②当印制证书超过2千个时，乙厂的印刷费用为0.2元/个；
③当印制证书8千个时，应选择乙厂，可节省费用500元．
其中正确的有（）

A、①② B、②③ C、①③ D、①②③

查看试题解析
4. 《九章算术》记载：今有坦高九尺，瓜生其上，蔓日长七寸；瓠生其下﹐蔓日长一尺.问几何日相逢?意思是有一道墙，高9尺，在墙头种一株瓜，瓜蔓沿墙向下每天长7寸（1尺=10寸）；同时地上种着瓠沿墙向上每天长1尺，问瓜蔓、瓠蔓要多少天才相遇？小李绘制如图的函数模型解决了此问题.图中h（单位：尺）表示瓜蔓与瓠蔓离地面的高度，x（单位：天）表示生长时间.根据小李的模型，点P的横坐标为（）

A、 $\frac{9}{8}$ B、 $\frac{90}{17}$ C、 $\frac{9}{17}$ D、 $\frac{17}{3}$

查看试题解析
5. 甲、乙两名运动员同时从 $A$ 地出发前往 $B$ 地，在笔直的公路上进行骑自行车训练如图所示，反映了甲、乙两名运动员在公路上进行训练时的行驶路程 $S$ (千米)与行驶时间 $t$ (小时)之间的关系，下列四种说法：①甲的速度为40千米/小时；②乙的速度始终为50千米/小时；③行驶1小时时，乙在甲前10千米处；④甲、乙两名运动员相距5千米时， $t = 0.5$ 或 $t = 2$ ．其中正确的个数有（）

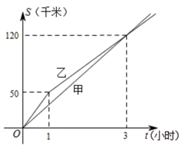A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 一个有进水管与出水管的容器，从某时刻开始的 $4 m i n$ 内只进水不出水，在随后的 $8 m i n$ 内既进水又出水，之后只出水不进水，每分的进水量和出水量是两个常数，容器内的水量y（单位： $L$ ）与时间x（单位： $m i n$ ）之间的关系如图．则下列说法正确的是（）

A、进水管每分钟的进水量为 $4 L$ B、当 $4 < x \leq 12$ 时， $y = \frac{5}{4} x + 12$ C、出水管每分钟的出水量为 $\frac{5}{4} L$ D、水量为 $15 L$ 的时间为 $3 m i n$ 或 $16 m i n$

查看试题解析
7. 某电信公司推出两种不同的收费标准：A种方式是月租20元；B种方式是月租0元．一个月本地网内打出电话费S（元）与打出时间t（分）的函数图象如图所示，当打出150分钟时，这两种方式的电话费相差（）

A、5元 B、10元 C、15元 D、20元

查看试题解析
8. 在物理实验课上，小宋利用滑轮组及相关器材进行实验，他把得到的拉力 $F (N)$ 和所悬挂物体的重力 $G (N)$ 的几组数据用电脑绘制成如图所示的图象 $($ 不计绳重和摩擦 $)$ ，请你根据图象判断以下结论不正确的是（）

A、施加的拉力 $F$ 随着物体重力 $G$ 的增加而增大 B、当拉力 $F = 2.7 N$ 时，物体的重力 $G = 3.5 N$ C、当物体的重力 $G = 7 N$ 时，拉力 $F = 4.5 N$ D、当滑轮组未悬挂物体在空中静止时，所用拉力为 $1 N$

查看试题解析
9. $A$ 、 $B$ 两地相距 $80 k m$ ，甲、乙两人沿同一条路从A地到 $B$ 地． $I_{1}$ ， $I_{2}$ 分别表示甲、乙两人离开 $A$ 地的距离 $s$ （ $k m$ ）与时间 $t$ （ $h$ ）之间的关系．对于以下说法：①乙车出发1.5小时后甲才出发；②两人相遇时，他们离开A地 $20 k m$ ；③甲的速度是 $40 k m / h$ ，乙的速度是 $\frac{40}{3} k m / h$ ；④当乙车出发2小时时，两车相距 $13 k m$ ．其中正确的结论有（）

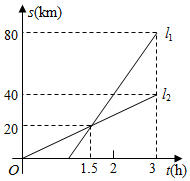A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 小亮从家步行到公交车站台，等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法不正确的是（）

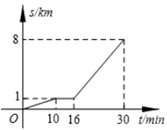A、他离家8km共用了30min B、他等公交车时间为6min C、他步行的速度是100m/min D、公交车的速度是350m/min

查看试题解析

二、填空题

11. 已知汽车装满油之后，油箱里的剩余油量y（升）与汽车行驶路程x（千米）之间的函数图象如图所示．为了行驶安全，油箱中的油量不能少于 $5$ （升），那么这辆汽车装满油后至多行驶（千米）后需要再次加油．

查看试题解析
12. 和谐号动车刹车后作匀减速运动，速度 $v (k m / m i n)$ 与刹车时间 $t (m i n)$ 与之间满足关系式 $v = - \frac{5}{4} t + 5$ ．动车在匀变速直线运动中，从开始刹车到准确停到站台，需要 $m i n$ ．

查看试题解析
13. 某苹果种植合作社通过网络销售苹果，如图所示的线段AB反映了苹果的日销售量y（千克）与销售单价x（元/千克）间的函数关系，已知1千克苹果的成本是5元，如果某天该合作社的苹果销售单价为8元/千克，那么这天销售苹果的盈利是元．

查看试题解析
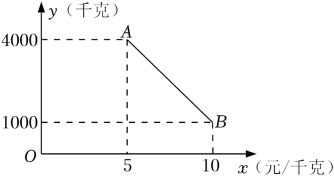14. 长沙向北京打长途电话，设通话时间x(分)，需付电话费y(元)，通话3分以内话费为3.6元.请你根据如图所示的y随x的变化的图象，找出通话5分钟需付电话费元.

查看试题解析
15. 已知某汽车油箱中的剩余油量 y (升)是该汽车行驶时间 t (小时)的一次函数，其关系如下表：
t （小时）
$0$
$1$
$2$
$3$
…
y （升）
$100$
$92$
$84$
$76$
…
由此可知，汽车行驶了小时，油箱中的剩余油量为 $8$ 升.

查看试题解析
16. 黄冈中学是百年名校，百年校庆上的焰火晚会令很多人记忆犹新．有一种焰火升高高度为h（m）与飞行时间t（s）的关系式是 $h = - \frac{5}{2} + 20 t + 1$ ，若这种焰火在点燃升空后到最高处引爆，则从点火到引爆所需时间为s．

查看试题解析

三、解答题

17. 暑假期间，两位家长计划带领若干名学生去旅游，他们联系了报价每人均为500元的两家旅行社．经协商，甲旅行社优惠条件是：两位家长全额收费，学生都按七折收费；乙旅行社的优惠条件是：家长、学生都按八折收费．假设这两位家长带领x名学生去旅游，他们应选择哪家旅行社？

查看试题解析
18. 某农户准备在一个大棚里种植甲、乙两种水果．实际种植中，甲种水果的种植费用y（元）与种植面积 $x (m^{2})$ 的函数关系如图所示，乙种水果的种植费用为每平方米20元．

(1)、求y与x的函数关系式；

(2)、甲、乙两种水果种植面积共 $600 m^{2}$ ，其中，甲种水果的种植面积x满足 $200 < x \leq 350$ ，怎样分配甲、乙两种水果种植面积才能使种植费用最少？最少种植费用是多少？

查看试题解析
19. “龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场 $.$ 图中的图象刻画了“龟兔再次赛跑”的故事 $(x$ 表示乌龟从起点出发所行的时间， $y_{1}$ 表示乌龟所行的路程， $y_{2}$ 表示兔子所行的路程 $)$ ．

(1)、“龟兔再次赛跑”的路程为米；

(2)、兔子比乌龟晚出发分钟；

(3)、乌龟在途中休息了分钟；

(4)、乌龟的速度是米 $/$ 分；

(5)、兔子的速度是米 $/$ 分；

(6)、兔子在距起点米处追上乌龟．

查看试题解析
20. 我市某店购进A ， B两种雨伞，已知购买A种雨伞30把，B种雨伞40把，共花费2900元，A种雨伞的单价比B种雨伞的单价高15元．

(1)、A ， B两种雨伞的单价分别是多少元？

(2)、商店决定再次购进A ， B两种雨伞共50把，正好赶上厂家进行促销活动，促销方式如下：A种雨伞按单价的八折出售，B种雨伞每把降价5元出售，如果此次购买A种雨伞的数量不低于B种雨伞数量的 $\frac{1}{3}$ ，那么应购买多少把A种雨伞，使此次购买雨伞的总费用最少？最少费用是多少元？

查看试题解析
21. 我市某公司产品销售量得到大幅提升．为促进生产，公司提供了两种付给员工月报酬的方案，如图所示，员工可以任选一种方案与公司签订合同．看图解答下列问题：

(1)、当 $x =$ __▲__时，两种方案付给的报酬一样多，并求方案二y关于x的函数表达式；

(2)、如果你是劳务服务部门的工作人员，你如何指导员工根据自己的生产能力选择方案．

查看试题解析
22. 遵义茶历史悠久，早从夜郎古国的茶马古道开始，遵义茶便从崇山峻岭中走出来，某茶叶店准备购买湄潭翠芽和湄江翠片两种茶叶进行销售，已知购买4千克湄潭翠芽和3千克湄江翠片需要2500元；购买2千克湄潭翠芽和5千克湄江翠片需要2300元．

(1)、求湄潭翠芽、湄江翠片两种茶叶的单价分别为多少？

(2)、该茶叶店计划购买湄潭翠芽、湄江翠片两种茶叶共80千克，总费用不超过26000元，并且要求湄潭翠芽数量不能低于10千克，最少费用为多少元？

查看试题解析

23. 学校决定按年级开展师生研学活动，该校八年级师生共580人将参加研学活动，计划租用12辆大客车，现有甲、乙两种型号的大客车，它们的满座载客量和租车费用如下表：

	甲型号大客车	乙型号大客车
满座载客量（人/辆）	55	35
租车费用（元/辆）	1200	800

(1)、若租用的12辆大客车恰好能一次将八年级师生送到研学基地，求应分别租用甲、乙型号的大客车多少辆？

(2)、设租用甲型号大客车x辆，租车总费用为y元．

①求出y（元）与x（辆）的函数关系式，并求出x的取值范围；

②当租用甲型号大客车多少辆时，租车的总费用最少，最少费用是多少？

查看试题解析

24. $2022$ 年4月16日，神舟十三号载人飞船返回舱成功着陆，任务取得圆满成功．航模店看准商机，推出了“神舟”和“天宫”模型．已知每个“天宫”模型的成本比“神舟”模型低 $20 %$ ，同样花费 $320$ 元，购进“天官”模型的数量比“神舟”模型多4个．

(1)、“神舟”和“天宫”模型的成本各多少元？

(2)、该航模店计划购买两种模型其 $100$ 个，且每个“神舟”模型的售价为 $34$ 元，“天官”模型的售价为 $26$ 元．设购买“神舟”模型a个，销售这批模型的利润为w元．
①求w与a的函数关系式（不要求写出a的取值范围）；
②若购进“神舟”模型的数量不超过“天官”模型数量的一半，则购进“神舟”模型多少个时，销售这批模型可以获得最大利润？最大利润是多少？

查看试题解析

t （小时）	$0$	$1$	$2$	$3$	…
y （升）	$100$	$92$	$84$	$76$	…