2025年广东省七年级数学下册预测押题卷(2)(人教版)

试卷更新日期：2025-06-10 类型：期末考试

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.

1. -8的立方根是（）

A、-2 B、2 C、±2 D、4

查看试题解析
2. 下列各组值中，是方程组 $\{\begin{array}{l} x + y = 3 \\ x - y = 1 \end{array}$ 的解的是（）

A、 $\{\begin{array}{l} x = 2 \\ y = 1 \end{array}$ B、 $\{\begin{array}{l} x = 1 \\ y = 2 \end{array}$ C、 $\{\begin{array}{l} x = 3 \\ y = 0 \end{array}$ D、 $\{\begin{array}{l} x = 4 \\ y = 3 \end{array}$

查看试题解析
3. 空气是由多种气体混合而成的，为了直观地介绍空气各成分的百分比，最适合使用的统计图是（）

A、条形图 B、扇形图 C、折线图 D、频数分布直方图

查看试题解析
4. 如图，这是体育委员对七年级 (5) 班的立定跳远成绩进行全面调查后绘成的统计图，如果把大于 $0.8 m$ 的成绩视为合格，再绘制一幅扇形统计图，那么“不合格”部分对应的圆心角度数是（）

A、 $50^{\circ}$ B、 $60^{\circ}$ C、 $90^{\circ}$ D、 $80^{\circ}$

查看试题解析
5. 下列句子中，属于命题的是（）

A、直线 $A B$ 和 $C D$ 垂直吗？ B、过线段 $A B$ 的中点 $C$ 作 $A B$ 的垂线 C、同旁内角不互补，两直线不平行 D、已知 $a^{2} = 1$ ，求 $a$ 的值

查看试题解析
6. 已知关于 $x$ ， $y$ 的方程组 ${\begin{matrix} x + m y = 7 ① \\ m x - y = 2 + m ② \end{matrix}$ ，将此方程组的两个方程左右两边分别对应相加，得到一个新的方程，当 $m$ 每取一个值时，就有一个方程，这些方程有一个公共解，这个公共解是（）

A、 ${\begin{array}{l} x = 4 \\ y = - 1 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = - 4 \end{array}$ C、 ${\begin{array}{l} x = 5 \\ y = - 4 \end{array}$ D、 ${\begin{matrix} x = - 5 \\ y = 4 \end{matrix}$

查看试题解析
7. 我国明代数学家程大位所著《算法统宗》中记载了一道有趣的题目：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”题目大意是：100个和尚分100个馒头，刚好分完.大和尚1人分3个馒头，小和尚3人分一个馒头.问大、小和尚各有多少人？若大和尚有x人，小和尚有y人.则下列方程或方程组中① ${\begin{array}{l} x + y = 100 \\ \frac{1}{3} x + 3 y = 100 \end{array}$ ；② ${\begin{array}{l} x + y = 100 \\ 3 x + \frac{1}{3} y = 100 \end{array}$ ；③3x+ $\frac{1}{3}$ （100-x）=100；④ $\frac{1}{3}$ y+3（100-y）=100正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 若 $| 2 x + y + 8 | + (x - 2 y)^{2} = 0$ ，则 $3 x - y$ 的值是（）

A、-6 B、-8 C、-10 D、-12

查看试题解析
9. 下列说法不一定成立的是（）

A、若 $a < b$ ，则 $a + c < b + c$ B、若 $a + c < b + c$ ，则 $a < b$ C、若 $a < b$ ，则 $a c^{2} < b c^{2}$ D、若 $a c^{2} < b c^{2}$ ，则 $a < b$

查看试题解析
10. 我们规定：在平面直角坐标系 $x O y$ 中，任意不重合的两点 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ 之间的折线距离为 $d (M ， N) = | x_{1} - x_{2} | + | y_{1} - y_{2} |$ ，例如图①中，点 $M (- 2 ， 3)$ 与点 $N (1 ， - 1)$ 之间的折线距离为 $d (M ， N) = | - 2 - 1 | + | 3 - (- 1) | = 3 + 4 = 7$ ．如图②，已知点 $P (3 ， - 4)$ 若点 $Q$ 的坐标为 $(t ， 2)$ ，且 $d (P ， Q) = 10$ ，则 $t$ 的值为（）

A、 $- 1$ B、 $5$ C、 $5$ 或 $- 13$ D、 $- 1$ 或 $7$

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分.

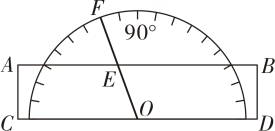
11. 直角坐标系中，点 $P (x ， y)$ 在第二象限，且 $P$ 到 $x$ 轴和 $y$ 轴的距离分别为 $3$ ， $4$ ，则点 $P$ 的坐标为．

查看试题解析
12. 如图，直尺的一边CD与量角器的零刻度线重合.如果量角器的一条刻度线OF的读数为70°，OF与AB相交于点E，那么∠AEF=°.

查看试题解析
13. 如图，在长为 $20 m$ ，宽为 $16 m$ 的长方形空地上，沿平行于各边分割出三个形状、大小一样的小长方形花圃，则其中一个小长方形花圃的长为m.

查看试题解析
14. 2018年全国滑冰场地与滑雪场地共有1133个．到了2021年，全国滑冰场地与滑雪场地共有2261个，其中滑冰场地比2018年滑冰场地的2倍多232个，滑雪场地比2018年滑雪场地增加了287个．求2018年全国滑冰场地和滑雪场地各有多少个．设2018年全国滑冰场地和滑雪场地分别有x个，y个，依据题意，可列二元一次方程组为．

查看试题解析
15. 对于一个各数位上的数字均不为0的三位自然数N，若N的十位数字等于百位和个位数字的差的绝对值，则称N是“差等中项数”，例如：三位数413，∵ $1 = | 4 - 3 |$ ， ∴413是“差等中项数”．把一个差等中项数N的任意一个数位上的数字去掉，得到三个两位数，这三个两位数之和记为 $F (N)$ ，把N的百位数字的3倍，十位数字的2倍和个位数字之和记为 $G (N)$ ．例如： $F (413) = 41 + 43 + 13 = 97$ ， $G (413) = 4 \times 3 + 1 \times 2 + 3 = 17$ ．已知三位数A是“差等中项数”， $\sqrt{F (A) - 2 G (A)}$ 是整数，则满足条件的所有A的个数是．

查看试题解析

三、解答题（一）：本大题共3小题，共25分.

16. 解方程组：

(1)、 $\{\begin{matrix} 2 y - 3 x = 1 ， \\ x - y = - 1 . \end{matrix}$

(2)、 $\{\begin{matrix} 3 (x + y) - 4 (x - y) = 4 ， \\ \frac{x + y}{2} + \frac{x - y}{6} = 1 . \end{matrix}$

查看试题解析
17. 计算： $- 1^{3} - \frac{1}{4} \times [1 - {(- 5)}^{2}] + \sqrt[3]{- 27}$

查看试题解析
18. 图1表示一条两岸彼此平行的河，直线l₁、l₂表示河的两岸，且l₁//l₂ ，现要在这条河上建一座桥（桥与河岸垂直），“桥”用线段表示。

(1)、如图1，在河岸C、E两点建两座桥CD、EF ，则CD和EF的大小为CDEF；

(2)、如图2，现要在这条河上建一座桥，桥建在何处才能使从游乐场A经过桥到河对岸B的路程最短?
亮亮的方法是：作AD⊥l₂交l₁、l₂于C，D两点.，在CD处建桥能使从游乐场A经过桥到河对岸B的路程最短；
木木的方法是：作AD⊥l₂交l₁、l₂于C，D两点，把线段CD平移至BE ，在BE处建桥能使从游乐场A经过桥到河对岸B的路程最短。
你认为谁的方法正确？并说明理由。

(3)、如图3，现要在这条河上建一座桥，桥建在何处才能使从村庄A经桥过河到村庄B的路程最短?画出示意图，并用平移的原理说明理由。

查看试题解析

四、解答题（二）：本大题共3小题，共30分.

19. 同庆中学为丰富学生的校园生活，准备从军跃体育用品商店一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），若购买3个足球和2个篮球共需310元，购买2个足球和5个篮球共需500元．

(1)、购买一个足球、一个篮球各需多少元？

(2)、根据同庆中学的实际情况，需从军跃体育用品商店一次性购买足球和篮球共96个，要求购买足球和篮球的总费用不超过5720元，这所中学最多可以购买多少个篮球？

查看试题解析
20. 已知 $A$ 、 $B$ 在数轴上对应的数分别用 $a$ 、 $b$ 表示，且 ${(\frac{1}{2} a b + 10)}^{2} + | a - 2 | = 0$ ，点 $P$ 是数轴上的一个动点．

(1)、求出 $A$ 、 $B$ 之间的距离；

(2)、若 $P$ 到点 $A$ 和点 $B$ 的距离相等，求出此时点 $P$ 所对应的数；

(3)、数轴上一点 $C$ 距 $A$ 点 $3 \sqrt{6}$ 个单位长度，其对应的数 $c$ 满足 $| a c | = - a c$ ．当 $P$ 点满足 $P B = 2 P C$ 时，求 $P$ 点对应的数．

查看试题解析
21. 中国是世界文明发源地之一，是举世闻名的礼仪之邦．一个民族，之所以在世界文明之林享誉千年，在于它独特而充满魅力的文化．为了弘扬优秀传统文化，某中学举办了传统文化知识大赛（全体同学都参与），其规则是：每位参赛选手回答100道选择题，答对一题得1分，不答或错答得0分，赛后抽取部分参赛选手的答题成绩（单位：分）进行了相关统计，整理并绘制成如下的统计图表：
组别
成绩 $(x)$
频数（人）
百分比
1
$50 \leq x < 60$
30
$a$
2
$60 \leq x < 70$
45
$15 %$
3
$70 \leq x < 80$
60
$b$
4
$80 \leq x < 90$
$m$
$40 %$
5
$90 \leq x \leq 100$
45
$15 %$
请根据以上信息，解答下列问题：

(1)、表中 $m =$ ， $a =$ ， $b =$ ；

(2)、补全频数分布直方图；

(3)、如果将其绘制成扇形统计图，请求出参赛成绩不低于90分这组所在扇形圆心角的度数．

查看试题解析

五、解答题（三）：本大题共2小题，共20分.

22. 阅读下面的文字，解答问题：
大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来．于是小明用（ $\sqrt{2}$ -1）来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．

又例如：∵ $\sqrt{4}$ ＜ $\sqrt{7}$ ＜ $\sqrt{9}$ ，即∵2＜ $\sqrt{7}$ ＜3，

∴ $\sqrt{7}$ 的整数部分是2，小数部分为（ $\sqrt{7}$ -2）．

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是．

(2)、 $\sqrt{5}$ 的小数部分为a， $\sqrt{13}$ 的整数部分为b，则a＋b- $\sqrt{5}$ 的值；

(3)、已知： $10 + \sqrt{3} = x + y$ ，其中x是整数，且 $0 ＜ y ＜ 1$ ，求 $x - y$ 的值．

查看试题解析
23. 问题情境：如图1， $A B ∥ C D$ ， $∠ P A B = 130 °$ ， $∠ P C D = 120 °$ ，求 $∠ A P C$ 度数．
小明的思路是：过 $P$ 作 $P E ∥ A B$ ，通过平行线性质来求 $∠ A P C$ ．

(1)、按小明的思路，易求得 $∠ A P C$ 的度数为度；（直接写出答案）

(2)、问题迁移：如图2， $A B ∥ C D$ ，点 $P$ 在射线 $O M$ 上运动，记 $∠ P A B = α$ ， $∠ P C D = β$ ，当点 $P$ 在 $B$ 、 $D$ 两点之间运动时，问 $∠ A P C$ 与 $α$ 、 $β$ 之间有何数量关系？请说明理由；

(3)、在（2）的条件下，如果点 $P$ 在 $B$ 、 $D$ 两点外侧运动时（点 $P$ 与点 $O$ 、 $B$ 、 $D$ 三点不重合），请直接写出 $∠ A P C$ 与 $α$ 、 $β$ 之间的数量关系．

查看试题解析

组别	成绩 $(x)$	频数（人）	百分比
1	$50 \leq x < 60$	30	$a$
2	$60 \leq x < 70$	45	$15 %$
3	$70 \leq x < 80$	60	$b$
4	$80 \leq x < 90$	$m$	$40 %$
5	$90 \leq x \leq 100$	45	$15 %$