2025年广东省七年级数学下册期末模拟卷(3)(人教版）

试卷更新日期：2025-06-10 类型：期末考试

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.

1. 如图，某污水处理厂要从A处把处理过的水引入排水渠 $P Q$ ，为了节约用料，铺设垂直于排水渠的管道 $A B$ ．这种铺设方法蕴含的数学原理是（）

A、两点确定一条直线 B、两点之间，线段最短 C、过一点可以作无数条直线 D、垂线段最短

查看试题解析
2. 在实数 $\sqrt{3}$ ， $- 1$ ， 0， $π$ 中，最大的数是（　　）

A、 $\sqrt{3}$ B、 $- 1$ C、0 D、 $π$

查看试题解析
3. 已知点 $M$ 在第二象限，它到 $x$ 轴的距离为2，到 $y$ 轴的距离为3，则点 $M$ 的坐标是（）

A、 $(2, - 3)$ B、 $(3, - 2)$ C、 $(- 3, 2)$ D、 $(- 2, 3)$

查看试题解析
4. 不等式组 $\{\begin{matrix} 3 m - 2 \geq 1, \\ 2 - m > 3 \end{matrix}$ 的解集在同一条数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 地理老师介绍到：长江比黄河长 836 千米，黄河长度的 6 倍比长江长度的 5 倍多 1284 千米. 小东根据地理老师的介绍，设长江长为 $x$ 千米，黄河长为 $y$ 千米，然后通过列、解二元一次方程组，正确地求出了长江和黄河的长度，那么小东列的方程组可能是（）

A、 $\{\begin{array}{l} x - y = 836 \\ 6 y - 5 x = 1284 \end{array}$ B、 $\{\begin{array}{l} x - y = 836 \\ 6 x - 5 y = 1284 \end{array}$ C、 $\{\begin{array}{l} x + y = 836 \\ 6 y - 5 x = 1284 \end{array}$ D、 $\{\begin{array}{l} x + y = 836 \\ 5 x - 6 y = 1284 \end{array}$

查看试题解析
6. 绿色出行，健康出行，你我同行，某县为了方便市民绿色出行，推出了共享单车服务，图①是共享单车放在水平地面的实物图，图②是其示意图，其中 $A B ， C D$ 都与地面平行， $∠ 1 = 52 °$ ， $∠ B A C = 48 °$ ，已知 $B C ∥ A M$ ，则 $∠ A C B$ 的度数为（）

A、 $80 °$ B、 $70 °$ C、 $68 °$ D、 $50 °$

查看试题解析
7. 图1是长方形纸条， $∠ D E F = α$ ，将纸条沿 $E F$ 折叠成折叠成图2，则图中的 $∠ G F C$ 的度数是（）

A、 $2 α$ B、 $90 ° + 2 α$ C、 $180 ° - 2 α$ D、 $180 ° - 3 α$

查看试题解析
8. 在平面直角坐标系中，将点 $(m, n)$ 先向右平移3个单位长度，再向上平移2个单位长度，最后所得点的坐标是（）

A、 $(m + 3, n - 2)$ B、 $(m + 3, n + 2)$ C、 $(m - 3, n - 2)$ D、 $(m - 3, n + 2)$

查看试题解析
9. 如图是红军长征路线图，如果表示会宁会师的点的坐标为 $(2, 2)$ ，表示吴起镇会师的点的坐标为 $(3, 3)$ ，则表示瑞金的点的坐标为（）

A、 $(6, 3)$ B、 $(3, 5)$ C、 $(6, - 3)$ D、 $(5, - 3)$

查看试题解析
10. 不等式组 ${\begin{matrix} 5 x - 3 < 3 x + 5 \\ x < a \end{matrix}$ 的解集为x＜4，则a满足的条件是（）

A、a＜4 B、a=4 C、a≤4 D、a≥4

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分.

11. 已知方程 $x^{a + 2} - y^{3 - b} = 2$ 是二元一次方程，则 $a + b =$ ．

查看试题解析
12. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格．将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等．如图所示是一个未完成的幻方，则 $x - y =$ ．

查看试题解析
13. $\sqrt{81}$ 的算术平方根是

查看试题解析
14. 已知关于x，y的二元一次方程组 ${\begin{matrix} 2 x + 3 y = k \\ x + 2 y = - 1 \end{matrix}$ 的解互为相反数，则k的值是．

查看试题解析
15. 如图，点 $A (0 ， 1)$ ，点 $A_{1} (2 ， 0)$ ，点 $A_{2} (3 ， 2)$ ，点 $A_{3} (5 ， 1)$ ，按照这样的规律下去，点 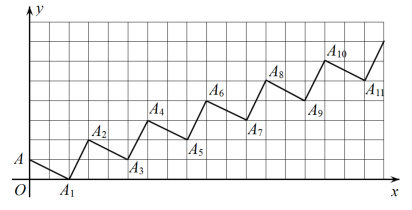$A_{2022}$ 的坐标为．

查看试题解析

三、解答题（一）：本大题共3小题，共21分.

16. 解方程组： ${\begin{cases} \frac{x}{2} - \frac{y + 1}{3} = 1 \\ 3 x + 2 y = 10 \end{cases}$

查看试题解析
17. 解不等式组 $\{\begin{matrix} 2 x - 5 < 3 (x - 1) ① \\ \frac{4}{3} x + 1 \leq 3 - \frac{2 x}{3} ② \end{matrix}$ ，并将解集表示在数轴上．

查看试题解析
18. 如图所示，在平面直角坐标系中 $x O y$ 中，点 $A (- 4, 1), △ A B C$ 的三个顶点都在格点上．将 $△ A B C$ 在坐标系中平移，使得点 $A$ 平移至图中点 $D (1, - 1)$ 的位置，点 $B$ 对应点 $E$ ，点 $C$ 对应点 $F$ ．

(1)、点 $B$ 的坐标为______，点 $F$ 的坐标为______；

(2)、在图中作出 $△ D E F$ ，并连接 $A D$ ；

(3)、求在线段 $A B$ 平移到线段 $D E$ 的过程中扫过的面积；

查看试题解析

四、解答题（二）：本大题共3小题，共29分.

19. 随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具．某汽车销售公司计划购进一批新能源汽车尝试进行销售，据了解2辆 $A$ 型汽车、3辆 $B$ 型汽车的进价共计80万元；3辆 $A$ 型汽车、2辆 $B$ 型汽车的进价共计95万元．

(1)、求A、B两种型号的汽车每辆进价分别为多少万元？

(2)、若该公司计划正好用200万元购进以上两种型号的新能源汽车（两种型号的汽车均购买），请你帮助该公司设计购买方案；

(3)、若该汽车销售公司销售1辆A型汽车可获利8000元，销售1辆B型汽车可获利5000元，在（2）中的购买方案中，假如这些新能源汽车全部售出，哪种方案获利最大？最大利润是多少元？

查看试题解析
20. 某市为提高学生参与体育活动的积极性，2016年9月围绕“你最喜欢的体育运动项目（只写一项）”这一问题，对初一新生进行随机抽样调查，下图是根据调查结果绘制成的统计图（不完整）．
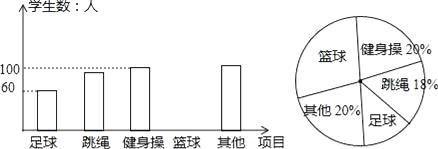
请你根据图中提供的信息解答下列问题：

(1)、本次抽样调查的样本容量是多少？

(2)、根据条形统计图中的数据，求扇形统计图中“最喜欢足球运动”的学生数所对应扇形的圆心角度数．

(3)、请将条形统计图补充完整．

(4)、若该市2016年约有初一新生18000人，请你估计全市本届学生中“最喜欢足球运动”的学生约有多少人．

查看试题解析
21. 【课本再现】据说，我国著名数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：一个数是 $59319$ ，要求它的立方根．华罗庚脱口而出： $39$ ．邻座的乘客十分惊奇，忙问计算的奥妙，华罗庚讲述了下列的计算过程：
第一步：因为 $10^{3} = 1000$ ， $100^{3} = 1000000$ ， $1000 < 59319 < 1000000$ ， $10 < \sqrt[3]{59319} < 100$ ．所以 $59319$ 的立方根是两位数；
第二步：因为 $59319$ 的个位上的数是 $9$ ，而在 $0$ ~ $9$ 中，只有 $9$ 的立方的个位上的数是 $9$ ，所以 $59319$ 的立方根的个位上的数是 $9$ ；
第三步：划去 $59319$ 后面的三位 $319$ 得到数 $59$ ，而 $3^{3} = 27$ ， $4^{3} = 64$ ， $27 < 59 < 64$ ，所以 $\sqrt[3]{59319}$ 的十位上的数是 $3$ ．
综上，可得 $\sqrt[3]{59319} = 39$ ．
【方法迁移】
第一步： $10^{3} = 1000$ ， $100^{3} = 1000000$ ，则 $15625$ 的立方根是________位数；
第二步： $15625$ 个位上的数字是 $5$ ，则 $15625$ 的立方根个位上的数字是________；
第三步：如果划去 $15625$ 后面的三位“ $625$ ”得到数 $15$ ，而 $2^{3} = 8$ ， $3^{3} = 27$ ，由此可确定 $15625$ 的立方根十位上的数字是________，因此 $15625$ 的立方根是________．
【解决问题】

(1)、将上述过程补充完整；

(2)、现在换一个数 $300763$ ，你能按这种方法得出它的立方根吗？如果能，请求出它的立方根，并写出必要的推理过程．

查看试题解析

五、解答题（三）：本大题共2小题，共25分.

22. 现有一块含 $30 °$ 角的直角三角尺 $A O B$ ， $∠ A O B$ 是直角，其顶点 $O$ 在直线 $l$ 上，请解决下列问题：

(1)、如图1，请直接写出 $∠ 1$ 、 $∠ 2$ 的数量关系；

(2)、如图2，分别过点 $A$ 、 $B$ 作直线 $l$ 的垂线，垂足分别为 $C$ 、 $D$ ，请写出图中分别与 $∠ 1$ 、 $∠ 2$ 相等的角，并说明理由；

(3)、如图3， $A C$ 平分 $∠ O A B$ ，将直角三角尺 $A O B$ 绕着点 $O$ 旋转，当 $A C ∥ l$ 时，请直接写出 $O B$ 与直线 $l$ 所成锐角的度数．

查看试题解析
23. 如图，在平面直角坐标系中，点A ， B的坐标分别为A（0，a），B（b ， a），且a ， b满足（a﹣3）²+|b﹣6|＝0，现同时将点A ， B分别向下平移3个单位，再向左平移2个单位，分别得到点A ， B的对应点C ， D ，连接AC ， BD ， AB ．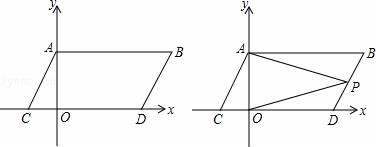

(1)、求点C ， D的坐标及四边形ABDC的面积S_{四边形ABCD}；

(2)、在y轴上是否存在一点M ，连接MC ， MD ，使S_△MCD＝ $\frac{1}{3}$ S_{四边形ABCD}？若存在这样一点，求出点M的坐标，若不存在，试说明理由；

(3)、点P是直线BD上的一个动点，连接PA ， PO ，当点P在BD上移动时（不与B ， D重合），直接写出∠BAP ， ∠DOP ， ∠APO之间满足的数量关系．

查看试题解析