2025年广东省八年级数学下册预测押题卷(2)(人教版)
试卷更新日期:2025-06-08 类型:期末考试
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 下列二次根式中属于最简二次根式的是( )A、 B、 C、 D、2. 定义运算“★”:对于任意实数a,b,都有 ★ = .若 , 则 ★ 的值为( )A、0 B、 C、 D、53. 我国是最早了解勾股定理的国家之一.据《周髀算经》记载,勾股定理的公式与证明是在商代由商高发现的,故又称之为“商高定理”;三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释,并给出了另外一个证明.下面四幅图中,不能证明勾股定理的是( )A、
 B、
B、 C、
C、 D、
D、 4. 已知方程 解是 ,则直线 与 的交点是( )A、(1,0) B、(1,3) C、(-1,-1) D、(-1,5)5. 在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数6. 正六边形蜂巢的建筑结构密合度最高、用材最少、空间最大、也最为坚固.如图,某蜂巢的房孔是边长为6的正六边形 , 点O是正六边形的中心,则的长为( )
4. 已知方程 解是 ,则直线 与 的交点是( )A、(1,0) B、(1,3) C、(-1,-1) D、(-1,5)5. 在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数6. 正六边形蜂巢的建筑结构密合度最高、用材最少、空间最大、也最为坚固.如图,某蜂巢的房孔是边长为6的正六边形 , 点O是正六边形的中心,则的长为( ) A、12 B、 C、 D、7. 如图,正方形的边长为 , 点和点在轴正半轴上,点、在第一象限,一次函数的图象交、分别于、 . 若与的面积比为 , 则的值为( )
A、12 B、 C、 D、7. 如图,正方形的边长为 , 点和点在轴正半轴上,点、在第一象限,一次函数的图象交、分别于、 . 若与的面积比为 , 则的值为( )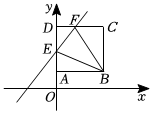 A、 B、 C、 D、8. 如图,在边长为1的正方形中,P是对角线上一点,连接 , 过点P作 , 交于点E,下列结论:①;②;③;④的最小值为 , 其中正确的是( ).
A、 B、 C、 D、8. 如图,在边长为1的正方形中,P是对角线上一点,连接 , 过点P作 , 交于点E,下列结论:①;②;③;④的最小值为 , 其中正确的是( ). A、①② B、①④ C、①②③ D、①②③④
A、①② B、①④ C、①②③ D、①②③④二、填空题:本大题共5小题,每小题3分,共15分.
-
9. 已知为正整数,且也为正整数,则的最小值为.10. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .
 11. 直线l: (k、b是常数, )经过 、 两点,其中 ,下列四个结论:①方程 的解在 和0之间;②若点 、 在直线l上,则 ;③ ;④不等式 的解集为 时, ,其中正确的结论有.(只需填写序号)12. 已知直线的解析式为 , 菱形 , , , …按图所示的方式放置,顶点 , , , , …均在直线上,顶点 , , , …均在轴上,则点的坐标是 .
11. 直线l: (k、b是常数, )经过 、 两点,其中 ,下列四个结论:①方程 的解在 和0之间;②若点 、 在直线l上,则 ;③ ;④不等式 的解集为 时, ,其中正确的结论有.(只需填写序号)12. 已知直线的解析式为 , 菱形 , , , …按图所示的方式放置,顶点 , , , , …均在直线上,顶点 , , , …均在轴上,则点的坐标是 .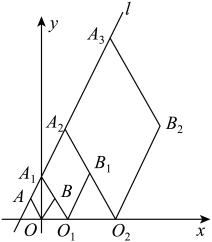 13. 定义:在平面直角坐标系中,若点M关于直线的对称点在的内部(不包含边界),则称点M是关于直线的“伴随点”.如图,已知三点,连接 , 以为边作 . 若在直线上存在点N,使得点N是关于直线的“伴随点”,则n的取值范围是 .
13. 定义:在平面直角坐标系中,若点M关于直线的对称点在的内部(不包含边界),则称点M是关于直线的“伴随点”.如图,已知三点,连接 , 以为边作 . 若在直线上存在点N,使得点N是关于直线的“伴随点”,则n的取值范围是 .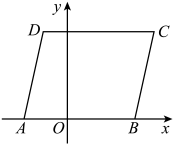
三、解答题(一):本大题共4小题,共36分.
-
14. 计算:(1)、 ;(2)、 .15. 先化简,再求值: , 其中 .16. 如图,已知四边形ABCD为正方形,AB= ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
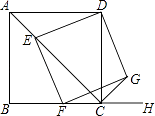
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
四、解答题(二):本大题共2小题,共18分.
-
17. 近年来,各种火灾事故频繁发生,掌握好消防安全知识,可以在火灾发生时起到重要作用.某校为了解学生对消防安全知识的掌握情况,对八年级共1500名同学进行了测试,现随机抽取八(1)班、八(2)班各15名同学的测试成绩(单位:分)进行整理,得到如下信息:
八(1)班15名学生测试成绩:78,83,85,87,89,90,92,93,94,95,97,98,99,100,100
八(2)班15名学生测试成绩其中有1人,有2人,有3人,有5人,有4人
八(1)和八(2)班测试成绩的平均数,中位数,众数,方差如下表所示:
班级
平均数
众数
中位数
方差
八(1)班
92
▲
▲
八(2)班
90
87
91
(1)、根据以上信息,补充完整表格中 , 的信息.(2)、若规定测试成绩90分及以上为优秀,请估计参加测试的1500名学生中成绩为优秀的学生共有多少人?(3)、根据以上数据,你认为哪个班的学生消防安全知识测试的整体成绩更好?请说明理由.18. 阅读材料,解决问题:把根式 进行化简,若能找到两个数m,n,满足 且 则可以把 变成 , 开方,从而使得 化简.
例如:化简
解:
(1)、化简:(2)、已知 1≤a≤2,化简:五、解答题(三):本大题共2小题,共21分.
-
19. 请阅读下列材料
问题:如图1,点A、B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小,小明的思路是:如图2所示,先作点A关于直线l的对称点A',使点A'、B分别位于直线l的两侧,再连接A'B,根据“两点间线段最短”可知A'B与直线l的交点P即为所求.
 (1)、如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D,若CP=1,AC=1,PD=2,求出AP+BP的值:(2)、将(1)中的条件“AC=1”去掉,换成“BD=4-AC”,其它条件不变,直接写出此时AP+BP的值:(3)、请结合图形,求 的最小值.20. 在直角坐标系中,如图1, , 点的坐标为 , , 点坐标为 , 点是射线上的动点,满足 , 以 , 为邻边作▱ .
(1)、如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D,若CP=1,AC=1,PD=2,求出AP+BP的值:(2)、将(1)中的条件“AC=1”去掉,换成“BD=4-AC”,其它条件不变,直接写出此时AP+BP的值:(3)、请结合图形,求 的最小值.20. 在直角坐标系中,如图1, , 点的坐标为 , , 点坐标为 , 点是射线上的动点,满足 , 以 , 为邻边作▱ . (1)、当时,求出的长度;(2)、当时,是否存在的值,使得▱的面积等于面积的 , 若存在,求出的值;若不存在,请说明理由;(3)、当点在第四象限时,点关于点的对称点为 , 点刚好落在直线上时,求的值直接写出答案 .
(1)、当时,求出的长度;(2)、当时,是否存在的值,使得▱的面积等于面积的 , 若存在,求出的值;若不存在,请说明理由;(3)、当点在第四象限时,点关于点的对称点为 , 点刚好落在直线上时,求的值直接写出答案 .