浙教版数学七年级下册期末模拟试题 B

试卷更新日期：2025-05-31 类型：期末考试

进入出卷网下载

一、选择题

1. 下列问题适合全面调查的是（　　）

A、调查市场上某品牌灯泡的使用寿命 B、了解全市人民对湖南省第二届旅发大会的关注情况 C、了解郴江河的水质情况 D、神舟十六号飞船发射前对飞船仪器设备的检查

查看试题解析
2. 计算： $\frac{4 a}{2 a - b} - \frac{2 b}{2 a - b} =$ （）

A、2 B、 $2 a - b$ C、 $\frac{2}{2 a - b}$ D、 $\frac{a - b}{2 a - b}$

查看试题解析
3. 如图，一块直角三角板的直角顶点放在直尺的一边上．如果 $∠ 1 = 70 °$ ，那么 $∠ 2$ 的度数是（　　）

A、 $20 °$ B、 $25 °$ C、 $30 °$ D、 $45 °$

查看试题解析
4. 国家“双减”政策实施后，某班开展了主题为“书香满校园”的读书活动．班级决定为在活动中表现突出的同学购买笔记本和碳素笔进行奖励（两种奖品都买）．其中笔记本每本3元，碳素笔每支2元，共花费28元，则共有几种购买方案（）

A、5 B、4 C、3 D、2

查看试题解析
5. 某校组织九年级学生赴韶山开展研学活动，已知学校离韶山50千米，师生乘大巴车前往，某老师因有事情，推迟了10分钟出发，自驾小车以大巴车速度的 $1.2$ 倍前往，结果同时到达．设大巴车的平均速度为x千米/时，则可列方程为（）

A、 $\frac{50}{x} = \frac{50}{1.2 x} + \frac{1}{6}$ B、 $\frac{50}{x} + 10 = \frac{50}{1.2 x}$ C、 $\frac{50}{x} = \frac{50}{1.2 x} + 10$ D、 $\frac{50}{x} + \frac{1}{6} = \frac{50}{1.2 x}$

查看试题解析
6. 分式 $\frac{x^{2} - x}{x - 1}$ 的值为0，则 $x$ 的值是（）

A、0 B、 $- 1$ C、1 D、0或1

查看试题解析
7. 解分式方程 $\frac{1}{x - 2}$ ﹣3= $\frac{4}{2 - x}$ 时，去分母可得（）

A、1﹣3（x﹣2）=4 B、1﹣3（x﹣2）=﹣4 C、﹣1﹣3（2﹣x）=﹣4 D、1﹣3（2﹣x）=4

查看试题解析
8. 已知 $2 a^{2} - a - 3 = 0$ ，则 $(2 a + 3) (2 a - 3) + (2 a - 1)^{2}$ 的值是（）

A、6 B、 $- 5$ C、 $- 3$ D、4

查看试题解析
9. 已知关于 $x$ 的分式方程 $\frac{x}{x - 1} - 2 = \frac{k}{1 - x}$ 的解为正数，则 $k$ 的取值范围为（）

A、 $- 2 < k < 0$ B、 $k > - 2$ 且 $k \neq - 1$ C、 $k > - 2$ D、 $k < 2$ 且 $k \neq 1$

查看试题解析
10. 如图，将两张边长分别为 $a$ 和 $b (a > b)$ 的正方形纸片按图 1，图 2 两种方式放置长方形内 (图 1，图 2 中两张正方形纸片均有部分重叠)，未被这两张正方形纸片覆盖的部分用阴影部分表示. 设图 1 中阴影部分面积为 $S_{1}$ ，图 2 中阴影部分面积为 $S_{2}$ . 当 $A B - A D = 3$ 时， $S_{1} - S_{2}$ 的值为 ( )

A、 $3 a$ B、 $3 a - 3 b$ C、 $- 3 b$ D、 $3 b$

查看试题解析

二、填空题（每题3分，共18分）

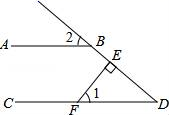
11. 如图，AB∥CD，FE⊥DB，垂足为E，∠1＝50°，则∠2的度数是.

查看试题解析
12. 因式分解： $2 x^{2} - 4 x =$ .

查看试题解析
13. 小芸为了解同学们最感兴趣的在线学习方式，设计了如下的调查问题（选项不完整）：你最感兴趣的一种在线学习方式是（）（单选）
$A$ ． $B$ ． $C$ ． $D$ ．其他
她准备从“①在线听课，②在线讨论，③在线学习 $2 ~ 3$ 小时，④用手机在线学习，⑤在线阅读”中选取三个作为该问题的备选答案，合理的选取是．（填序号）

查看试题解析
14. 若关于 $x$ 的分式方程 $\frac{x + 1}{x - 3} = 2 - \frac{a}{3 - x}$ 有增根，则 $a$ 的值为

查看试题解析
15. 如图摆放的一副学生用直角三角板， $∠ E = 60 °$ ， $∠ B = 45 °$ ， $A B$ 与 $D E$ 相交于点G，当 $E F ∥ B C$ 时，则 $∠ E G B$ 的度数是．

查看试题解析
16. 如果一个自然数 $A$ 能分解成： $A = M \times N$ ，其中 $M$ 和 $N$ 都是两位数，且 $M$ 与 $N$ 的十位数字之和为 $8$ ，个位数字之和为 $7$ ，则称 $A$ 为“霸气数”，把 $A$ 分解成 $A = M \times N$ 的过程叫做“霸气分解”．例如：因为 $1472 = 23 \times 64$ ， $2 + 6 = 8$ ， $3 + 4 = 7$ ，所以 $1472$ 是“霸气数”；因为 $391 = 23 \times 17$ ， $2 + 1 \neq 8$ ，所以 $391$ 不是“霸气数”，则最大的“霸气数”为；若自然数 $A$ 是“霸气数”，“霸气分解”为 $A = M \times N$ ，将 $M$ 的个位数字与 $N$ 的十位数字之和记为 $P (A)$ ，将 $M$ 的十位数字与 $N$ 的个位数字之和记为 $Q (A)$ ，若 $\frac{P (A)}{Q (A)}$ 为整数，则满足条件的自然数 $A$ 的最大值为．

查看试题解析

三、解答题（共8题，共72分）

17. 分解因式：

(1)、 $5 a^{2} - 20 b^{2};$

(2)、 ${(2 n + 1)}^{2} - {(3 n - 1)}^{2} 。$

查看试题解析
18. 解方程： $\frac{3}{x + 2} + 1 = \frac{x}{x - 2}$ ．

查看试题解析
19. 计算： $\frac{x^{2} - 9}{x^{2} + 2 x + 1} \div (x + \frac{3 - x^{2}}{x + 1})$ ．

查看试题解析

20. 金师傅近期准备换车，看中了价格相同的两款国产车．

燃油车油箱容积：40升，油价：9元／升，续航里程： $a$ 千米，每千米行驶费用： $\frac{40 \times 9}{a}$ 元；

新能源车电池电量：100千瓦时，电价：0.6元／千瓦时，续航里程： $a$ 千米，每千米行驶费用： ▲ 元．

(1)、用含

a

的代数式表示新能源车的每千米行驶费用；

(2)、若燃油车的每千米行驶费用比新能源车多0.5元．

①分别求出这两款车的每千米行驶费用．

②若燃油车和新能源车每年的其它费用分别为4800元和7500元．问：每年行驶里程为多少千米时，买新能源车的年费用更低？（年费用=年行驶费用+年其它费用）

查看试题解析

21. 根据规律答题．
小明同学在一次教学活动中发现：方程 $x + \frac{1}{x} = 2 + \frac{1}{2}$ 的解为 $x_{1} = 2, x_{2} = \frac{1}{2}$ 方程 $x + \frac{1}{x} = 3 + \frac{1}{3}$ 的解为 $x_{1} = 3, x_{2} = \frac{1}{3}$ 方程 $x + \frac{1}{x} = 4 + \frac{1}{4}$ 的解为 $x_{1} = 4, x_{2} = \frac{1}{4} \dots \dots$
以此类推：

(1)、请你依据小明的发现，猜想关于x 的方程 $x + \frac{1}{x} = 8 + \frac{1}{8}$ 的解是______；

(2)、根据上述的规律，猜想由关于x 的方程 $x + 1 + \frac{1}{x + 1} = a + \frac{1}{a} (a \neq 0)$ 得到 $x + 1 =$ ________；

(3)、拓展延伸：由（2）可知，在解方程 $x + \frac{x + 2}{x + 1} = \frac{82}{9}$ 时，可变形转化为 $x + \frac{1}{x} = a + \frac{1}{a}$ 的形式求值，按要求写出你的变形求解过程．

查看试题解析
22. 电视剧《一代洪商》在中央电视台第八套播出后，怀化市各旅游景点知名度得到显菩提高.为全面提高旅游服务质量，旅游管理部门随机抽取了100名游客进行满意度调查，并绘制成如下不完整的频数分布表和扇形统计图.
频数分布表
满意程度
频数（人）
频率
非常满意
50
0.5
满意
30
0.3
一般
a
c
不满意
b
0.05
合计
100
1
根据统计图表提供的信息，解答下列问题：

(1)、a＝， b＝， c＝；

(2)、求扇形统计图中表示“一般”的扇形圆心角α的度数；

(3)、根据调查情况，请你对各景点的服务提一至两条合理建议.

查看试题解析
23. 如图，直线 $P Q ∥ M N$ ，一副三角尺（ $∠ A B C = ∠ C D E = 90 °$ ， $∠ A C B = 30 °$ ， $∠ B A C = 60 °$ ， $∠ D C E = ∠ D E C = 45 °$ ）按如图①放置，其中点E在直线 $P Q$ 上，点B，C均在直线 $M N$ 上，且 $C E$ 平分 $∠ A C N$ ．
AI

(1)、求 $∠ D E Q$ 的度数．

(2)、如图②，若将三角形 $A B C$ 绕点B以每秒4度的速度按逆时针方向旋转（A，C的对应点分别为F，G），当 $B G$ 落在射线 $B M$ 上时，立即以原速按顺时针方向旋转，当 $B G$ 落在射线 $B N$ 上时，运动停止．设旋转时间为t（s）．
①在旋转过程中，若边 $B G ∥ C D$ ，求t的值．
②若在三角形 $A B C$ 绕点B旋转的同时，三角形 $C D E$ 绕点E以每秒1度的速度按顺时针方向旋转（C，D的对应点为H，K），两个三角形同时停止运动．请直接写出当 $∠ G B N$ 的角平分线与 $∠ H E K$ 的角平分线平行时t的值．

查看试题解析