锐角三角函数-【考前20天】2025年中考数学终极冲刺专题
试卷更新日期:2025-05-27 类型:三轮冲刺
一、填空题
-
1. 如图,在中, , 是的角平分线,点E在上,过点E作 , 交于点F.若 , , , 则 .
 2. 如图,在中, , , 点D为斜边AC上一点,连接BD,将沿BD翻折得到 , BE与AC交于点F,当时,则.
2. 如图,在中, , , 点D为斜边AC上一点,连接BD,将沿BD翻折得到 , BE与AC交于点F,当时,则. 3. 如图,在菱形中, , 其顶点落在反比例函数的图象上,顶点落在轴的正半轴上,顶点落在反比例函数的图象上,则的值为 .
3. 如图,在菱形中, , 其顶点落在反比例函数的图象上,顶点落在轴的正半轴上,顶点落在反比例函数的图象上,则的值为 . 4. 如图,身高1.6米的小亮站在点测得旗杆的仰角为 , 小亮向旗杆走了6米到达点,测得旗杆的仰角为 , 则旗杆的高度为米.( , , )
4. 如图,身高1.6米的小亮站在点测得旗杆的仰角为 , 小亮向旗杆走了6米到达点,测得旗杆的仰角为 , 则旗杆的高度为米.( , , ) 5. 如图,在矩形中, , , , 是边上两点,且 , , 连接 , , 和交于点 , 连接 , 则的值是 .
5. 如图,在矩形中, , , , 是边上两点,且 , , 连接 , , 和交于点 , 连接 , 则的值是 . 6. 如图,在平面直角坐标系中,抛物线的图象与轴分别交于点和点 , 过顶点的直线轴于点 , 点为线段上一点,点在线段上,且 , 当取最小值时,则 .
6. 如图,在平面直角坐标系中,抛物线的图象与轴分别交于点和点 , 过顶点的直线轴于点 , 点为线段上一点,点在线段上,且 , 当取最小值时,则 .
二、选择题
-
7. 如图,梯子 , 梯子与地面的夹角为 , 则两梯脚之间的距离为( )
 A、 B、 C、 D、8. 在中,若角 , 满足 , 则的大小是( )A、 B、 C、 D、9. 图1、图2分别是某种型号跑步机的实物图与示意图.已知跑步机手柄AB与地面DE平行,支架AC、踏板CD的长分别为a,b,∠ACD=90°,记CD与地面DE的夹角为θ,则跑步机手柄AB所在直线与地面DE之间的距离表示正确的是( )
A、 B、 C、 D、8. 在中,若角 , 满足 , 则的大小是( )A、 B、 C、 D、9. 图1、图2分别是某种型号跑步机的实物图与示意图.已知跑步机手柄AB与地面DE平行,支架AC、踏板CD的长分别为a,b,∠ACD=90°,记CD与地面DE的夹角为θ,则跑步机手柄AB所在直线与地面DE之间的距离表示正确的是( ) A、 B、 C、 D、10. 如图、点分别是正方形边上的点,且 . 连接并延长,交的延长线于点M,设 , 则( )
A、 B、 C、 D、10. 如图、点分别是正方形边上的点,且 . 连接并延长,交的延长线于点M,设 , 则( ) A、 B、 C、 D、11. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.点E为小正方形的顶点,延长交于点F,分别交 , 于点G,H,过点D作的垂线交延长线于点K,连结 . 若为等腰三角形, , 则的值为( )
A、 B、 C、 D、11. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.点E为小正方形的顶点,延长交于点F,分别交 , 于点G,H,过点D作的垂线交延长线于点K,连结 . 若为等腰三角形, , 则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
12. 我国生产的无人机畅销世界,树立了良好的品牌形象,在一座高架桥的修建过程中,需要测量一条河的宽度 , 工作人员使用无人飞机通过设备在P处测得M , N两处的俯角分别为和 , 测得无人机离水平地面的高度为240米,若Q , M , N三点在同一条水平直线上,则这条河的宽度为多少米?(参考数据: , , 结果保留整数)
 13. 长沙香炉洲大桥全线长约三千米,横跨湘江,连通大泽湖街道和丁字湾街道,其中西汊航道独塔斜拉桥塔高202米,刷新了长沙跨江大桥的最高纪录.某校数学实践小组的同学利用课余时间对该桥进行了实地测量,得到如下数据: , , 米.
13. 长沙香炉洲大桥全线长约三千米,横跨湘江,连通大泽湖街道和丁字湾街道,其中西汊航道独塔斜拉桥塔高202米,刷新了长沙跨江大桥的最高纪录.某校数学实践小组的同学利用课余时间对该桥进行了实地测量,得到如下数据: , , 米. (1)、求的长;(2)、若一辆小车以15米/秒的速度从A往B行驶,问小车能否在40秒钟内通过路段?(参考数据: , , )
(1)、求的长;(2)、若一辆小车以15米/秒的速度从A往B行驶,问小车能否在40秒钟内通过路段?(参考数据: , , )四、实践探究题
-
14. 综合与实践
在综合与实践课上,数学兴趣小组通过测算某热气球的高度,探索实际生活中测量高度(或距离)的方法.
【实践活动】如图1,小明、小充分别在点B,C处同时测得热气球A的仰角 , , , 点B,C,D在地面的同一条直线上,于点D.(测角仪的高度忽略不计)
 (1)、【问题解决】计算热气球离地面的高度AD.(参考数据: , , )(2)、【方法归纳】小亮发现,原来利用解直角三角形的知识可以解决实际生活中的测量问题,其一般过程为:从实际问题抽象出数学问题,再通过解直角三角形得出实际问题的答案.
(1)、【问题解决】计算热气球离地面的高度AD.(参考数据: , , )(2)、【方法归纳】小亮发现,原来利用解直角三角形的知识可以解决实际生活中的测量问题,其一般过程为:从实际问题抽象出数学问题,再通过解直角三角形得出实际问题的答案.爱思考的小明类比该方法求得锐角三角形一边上的高. 根据他的想法与思路,完成以下填空:
如图2,在锐角三角形ABC中,设 , , , 于点D,用含 , 和m的代数式表示AD.
解:设 , 因为 ,
所以.
同理,因为 ,
所以①.
因为 ,
解得②.
即可求得AD的长.
15. 在平行四边形中,点 , 分别在边 , 上. (1)、【尝试初探】
(1)、【尝试初探】如图1,若平行四边形是正方形,为的中点, , 求的值;
(2)、【深入探究】如图2, , , , 求的值;
(3)、【拓展延伸】如图3,与交于点 , , , , 求的值.
五、证明题
-
16. 如图,在中, , 交于点 , 点为中点,连接 .
 (1)、求证:;(2)、若 , 求的长.17. 如图,为的直径,点C、点D为上异于A、B的两点,连接 , 过点C作 , 交的延长线于点E,连接、 .
(1)、求证:;(2)、若 , 求的长.17. 如图,为的直径,点C、点D为上异于A、B的两点,连接 , 过点C作 , 交的延长线于点E,连接、 . (1)、若 , 求证:是的切线.(2)、连接 , 若 , , 求的半径长.
(1)、若 , 求证:是的切线.(2)、连接 , 若 , , 求的半径长.六、阅读理解题
-
18. 阅读下面的材料,并回答所提出的问题:如图所示,在锐角三角形中,求证:
这个三角形不是一个直角三角形,不能直接使用锐角三角函数的知识去处理,所以必须构造直角三角形,过点A作 , 垂足为D,则在和中由正弦定义可完成证明.
解:如图,过点A作 , 垂足为D,

在中, , 则
中, , 则
所以 , 即
(1)、在上述分析证明过程中,主要用到了下列三种数学思想方法的哪一种( )A、数形结合的思想; B、转化的思想; C、分类的思想(2)、用上述思想方法解答下面问题.在中, , 求和的面积.
(3)、用上述结论解答下面的问题(不必添加辅助线)在锐角三角形中, , 求的度数.
19. (阅读理解)设点 在矩形 内部,当点 到矩形的一条边的两个端点距离相等时,称点 为该边的“和谐点”.例如:如图1,矩形 中,若 ,则称 为边 的“和谐点”.(解题运用)已知,点 在矩形 内部,且 , .
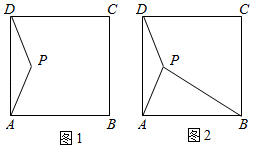 (1)、设 是边 的“和谐点”,则 ▲ 边 的“和谐点”(填“是”或“不是”);连接 , ,求 的值.(2)、若 是边 的“和谐点”,连接 , ,当 时,求 的值;(3)、如图2,若 是边 的“和谐点”,连接 ; , ,求 的最大值.
(1)、设 是边 的“和谐点”,则 ▲ 边 的“和谐点”(填“是”或“不是”);连接 , ,求 的值.(2)、若 是边 的“和谐点”,连接 , ,当 时,求 的值;(3)、如图2,若 是边 的“和谐点”,连接 ; , ,求 的最大值.