图形变换-【考前20天】2025年中考数学终极冲刺专题

试卷更新日期：2025-05-27 类型：三轮冲刺

进入 出卷网 下载

一、选择题

  • 1. 2025年碳中和目标加速推进，下列图标中既是轴对称图形又是中心对称图形的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 如图，将△ABC绕点A逆时针旋转55°得到△ADE ， 若AD⊥BC于点F ， 则∠B的度数为（      ）

    A、25° B、30° C、35° D、40°

    查看试题解析

  • 3.  如图，在四边形ABCD中，AB//CD，∠D=90°，∠B=45°，点E为CD上一点，连结AE，把AE绕点E逆时针旋转90°，点A恰好落在BC的中点F处，则AFAB的值为（  ）

    A、53 B、63 C、34 D、104

    查看试题解析

二、填空题

三、作图题

  • 4. 如图，在直角坐标系中，△ABC各顶点的横、纵坐标都是整数，

       

    (1)、作出△ABC关于x轴对称的图形△A1B1C1；
    (2)、求△ABC的面积

    查看试题解析

四、解答题

  • 5. 如图，在△ABC中，CA=CB,D是△ABC内一点，连结CD ， 将线段CD绕点C逆时针旋转到CE ， 使∠DCE=∠ACB ， 连结AD,DE,BE.

    (1)、求证：△CAD≅△CBE.
    (2)、当∠CAB=60°时，求∠CBE与∠BAD的度数和.

    查看试题解析

五、实践探究题

  • 6. 综合与实践

    【发现问题】在进行综合与实践活动时，学习小组发现生活中常用的A4纸是一个长与宽的比为2的矩形．

    【定义】若一个四边形为矩形，且长与宽的比为2 ， 则这个四边形为类A4矩形．

    【提出问题】如何用不同形状的纸折一个类A4矩形？

    (1)、【分析并解决问题】

    学习小组利用一张A4纸ABCD对折一次，使AB与DC重合，折叠过程如图1所示，其中AB=a,AD=2a ． 求证：四边形CDMN是类A4矩形；

    (2)、学习小组利用一张正方形纸片ABCD折叠2次，展开后得折痕BD，DE ， 再将其沿FG折叠，使得点B与点E重合，折叠过程如图2所示．求证：四边形CDFG是类A4矩形；

    (3)、【拓展】

    如图3，四边形ABCD纸片中，AC垂直平分BD,AC=102,BD=10 ， 点E，F，G ， H分别是边AB，BC，CD，DA上的点，将四边形ABCD纸片沿EF折叠，使得点B的对应点落在BD上，再沿FG，GH折叠，使得点C，D的对应点分别落在AC，BD上，若四边形EFGH是类A4矩形，请直接写出EF的值．

    查看试题解析

六、阅读理解题

  • 7. 阅读下列材料，并按要求完成相应的任务．

    你知道“皮克定理”吗？

    “皮克定理”是奥地利数学家皮克（如图1）发现的一个计算点阵中多边形的面积公式．在一张方格纸上，上面画着纵横两组平行线，相邻平行线之间的距离都相等，这样两组平行线的交点，就是所谓格点．一个多边形的顶点如果全是格点，这个多边形就叫做格点多边形．有趣的是，这种格点多边形的面积计算起来很方便，只要数一下图形边线上的点的数目及图内的点的数目，就可用公式算出．即 S=a+12b−1 ，其中a表示多边形内部的点数，b表示多边形边界上的点数，S表示多边形的面积．（利用图2中的多边形可以验证）这个公式是奥地利数学家皮克在1899年发现的，被称为“皮克定理”．

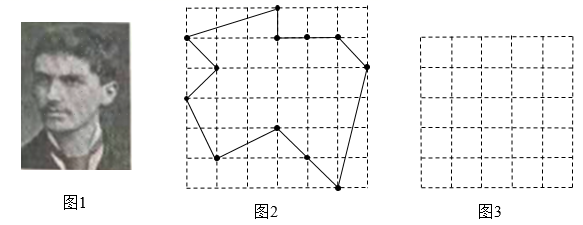
    任务：

    (1)、如图2，是 6×6 的正方形网格，且小正方形的边长为1，利用“皮克定理”可以求出图中格点多边形的面积是 ．
    (2)、已知：一个格点多边形的面积S为19，且边界上的点数b是内部点数a的3倍，则 a+b= ．
    (3)、请你在图3中设计一个格点多边形．要求：①格点多边形的面积为8；②格点多边形是一个轴对称图形．

    查看试题解析

七、综合题

  • 8. 在矩形ABCD的CD边上取一点E，将△BCE沿BE翻折，使点C恰好落在AD边上点F处．

    (1)、如图1，若BC=2BA，求∠CBE的度数；
    (2)、如图2，当AB=5，且AF•FD=10时，求BC的长；
    (3)、如图3，延长EF，与∠ABF的角平分线交于点M，BM交AD于点N，当NF=AN+FD时，求ABBC的值．

    查看试题解析