四边形之矩形与正方形-【考前20天】2025年中考数学终极冲刺专题

试卷更新日期：2025-05-27 类型：三轮冲刺

进入出卷网下载

一、选择题

1. 如图，正方形ABCD由四个全等的直角三角形（ $△ A B E, △ B C F$ ， $△ C D G, △ D A H)$ 和中间一个小正方形EFGH组成，连结BH ，若 $F G = 1, C D = 5$ ，则BH的长为（）

A、 $\sqrt{5}$ B、 $2 \sqrt{2}$ C、3 D、 $\sqrt{10}$

查看试题解析
2. 如图，在矩形ABCD中，BC>AB，先以点A为圆心，AB长为半径画弧交边AD于点E；再以点D为圆心，DE长为半径画弧交边DC于点F；最后以点C为圆心，CF长为半径画弧交边BC于点G.求BG的长，只需要知道（）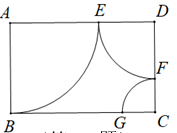

A、线段AB的长 B、线段AD的长 C、线段DE的长 D、线段CF的长

查看试题解析
3. 如图，在矩形ABCD中，AB=8，BC=4，点O为对角线BD的中点，E为线段AB上一点，连结EO，并延长交DC于点F，以点F为圆心，适当长为半径画弧，交FD于点M，交EF于点N。再以点N为圆心，MN长为半径画弧，两弧交于点P，连结FP，并延长交线段AB于点Q。则下列两个命题中说法正确的是（）
①△QEF为等腰三角形：②设AE长为x，BQ长为y，则（4-x）（4-y）=4。

A、①正确，②正确 B、①正确，②错误 C、①错误，②正确 D、①错误，②错误

查看试题解析

二、填空题

三、作图题

4. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A G$ 为 $△ A B C$ 的外角 $∠ B A E$ 的平分线， $B F ⊥ A G$ ，垂足为 $F$ ，点 $D$ 为 $B C$ 上一点，连接 $D F$ ，交 $A B$ 于点 $O$ ．

(1)、在不添加新的线的前提下，请增加一个条件：______，使得四边形 $A F B D$ 为矩形，并说明理由；

(2)、若四边形 $A F B D$ 为矩形，请用尺规作图的方法作一个菱形 $A B P C$ ，使 $B C$ 为菱形的一条对角线．（保留作图痕迹，不写作法）

查看试题解析

四、解答题

5. 如图， $△ A B C$ 中， $A B = A C$ ， $A D$ 平分 $∠ B A C$ ， $B E ∥ A D$ ， $A E ⊥ A D$ ．

(1)、求证：四边形 $A D B E$ 是矩形；

(2)、作 $E F ⊥ A B$ 于F，若 $B C = 4$ ， $A D = 3$ ，求 $E F$ 的长．

查看试题解析
6. 如图，O是矩形ABCD的对角线的交点，E，F，G，H分别是OA，OB，OC，OD上的点，且AE＝BF＝CG＝DH.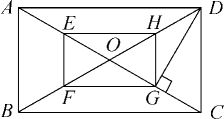

(1)、求证：四边形EFGH是矩形；

(2)、若E，F，G，H分别是OA，OB，OC，OD的中点，且DG⊥AC，OF＝2cm，求矩形ABCD的面积．

查看试题解析

五、实践探究题

7.

(1)、【新知探究】
对于正数 $a, b$ ，我们称 $\frac{a + b}{2}$ 为 $a, b$ 的算术平均数，称 $\sqrt{a b}$ 为 $a, b$ 的几何平均数．请观察下面的表格，并解答下面的问题：
$a, b$ 的值
$\frac{a + b}{2}$ 的值
$\sqrt{a b}$ 的值
$a = 2, b = 8$
5
4
$a = 4, b = 4$
4
4
$a = 6, b = 2$
4
m
$a = 5, b = 1$
3
$\sqrt{5}$
①表格中的 $m =$     ▲    ；
②根据表格，猜想 $a + b$ 与 $2 \sqrt{a b}$ 的大小关系（   ）；
A $．$ $a + b > 2 \sqrt{a b}$         B $．$ $a + b < 2 \sqrt{a b}$         C $．$ $a + b \geq 2 \sqrt{a b}$         D $．$ $a + b \leq 2 \sqrt{a b}$
③当 $a, b$ 满足条件：    ▲    时， $a^{2} + b^{2} = 2 a b$ ；

(2)、【理解应用】
①已知， $10 < x < 30$ ，当 $x =$     ▲    时，代数式 $(x - 10) (30 - x)$ 取得最大值是    ▲    ；
②如图1，已知，在Rt $△ A B C$ 中， $∠ C = 9 0^{°}$ ， $A B = 6$ ，求 $△ A B C$ 周长的最大值．

(3)、【拓展提升】
如图2，已知正方形ABCD的边长为4， $P$ 为CD边上的动点，PA交BD于 $E$ ，过点 $E$ 作 $E F ⊥ A P$ 交BC边于点 $F$ ，连AF交BD于点 $G$ ，则 $△ A G E$ 面积的最小值是    ▲     ．

查看试题解析

六、阅读理解题

七、综合题

8. 已知平行四边形 $A B C D$ ， $∠ B A D = α$ ，点E为对角线 $B D$ 上一动点，连接 $A E$ ，以 $A E$ 为一边在 $A E$ 的右侧作 $△ A E F$ ，使 $∠ A E F = α$ ，连接 $D F$ ．

(1)、若 $A B = A D$ 且 $α = 60 °$ ，当 $A E = E F$ ，如图①，求此时 $∠ A D F$ 度数；

(2)、若 $A B = A D$ 且 $α = 90 °$ ，当 $A E = E F$ ， $B E > D E$ 时，如图②，判断C，D，F三点是否共线并说明理由；

(3)、如图③若 $A B = 4$ ， $A D = 4 \sqrt{3}$ 且 $α = 90 °$ ， $∠ A F E = 30 °$ ，当 $△ C E F$ 是以 $E F$ 为底的等腰三角形时，直接写出 $△ B C E$ 的面积．

查看试题解析