四边形之平行四边形与菱形-【考前20天】2025年中考数学终极冲刺专题-在线组卷题库

1. 如图，在菱形 $A B C D$ 中， $E$ ， $F$ 分别是 $A C$ ， $C D$ 的中点， $A B = 8$ ，则 $E F$ 的长为( )

A、 $4$ B、 $6$ C、 $8$ D、不确定

查看试题解析
2. 如图，点B是正八边形的边 $A F$ 上一点，一束光线从点B出发，经过两次反射后到达边 $A G$ 上一点E ，若 $∠ A B C = 65 °$ ，则 $∠ A E D =$ （）

A、 $70 °$ B、 $65 °$ C、 $55 °$ D、 $60 °$

查看试题解析
3. 如图， $P$ 为 $▱ A B C D$ 的对角线 $B D$ 上一点，过点 $P$ 作 $A B$ ， $B C$ 的平行线，分别交 $A D$ ， $B C$ ， $A B$ ， $C D$ 于 $E, F, G, H$ 四点，连结 $A P, F H$ ．若 $△ A P E$ 的面积为 $2.5$ ，则 $△ P F H$ 的面积为（）

A、5 B、2.5 C、2.4 D、1.25

查看试题解析
4. 在菱形ABCD中，点E ， F分别是AB ， AD的中点，连接CE ， CF.若 $s i n ∠ E C F = \frac{3}{5}$ ， $C E = 10$ ，则BC的长为（）

A、 $4 \sqrt{5}$ B、 $4 \sqrt{3}$ C、 $3 \sqrt{6}$ D、6

查看试题解析
5. 如图， $△ A B C$ 中， $∠ A B C$ 为钝角，以 $A B$ 为边向外作平行四边形 $A B D E$ ， $∠ A B D$ 为钝角，连结 $C E$ ， $C D$ ，设 $△ C D E$ ， $△ A C E$ ， $△ B C D$ 的面积分别为 $S$ ， $S_{1}$ ， $S_{2}$ ，若知道 $△ A B C$ 的面积，则下列代数式的值可求的是（）

A、 $S + S_{1} + S_{2}$ B、 $S - S_{1} + S_{2}$ C、 $S + S_{1} - S_{2}$ D、 $S - S_{1} - S_{2}$

查看试题解析
6. 如图，菱形ABCD中，∠BAD＝60°，AC与BD交于点O，E为CD延长线上的一点，且CD＝DE，连接BE分别交AC，AD于点F、G，连接OG，则下列结论正确的是（）
① $O G = \frac{1}{2} A B$ ；②与 $△$ EGD全等的三角形共有2个；③S_四边形ODEG＝S_四边形ABOG；④由点A、B、D、E构成的四边形是菱形；

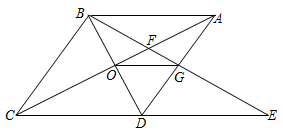A、①③④ B、①④ C、①②③ D、②③④

查看试题解析

7. 如图，在 $△ A B C$ 中， $A C = B C = 5, A B = 6, E F$ 分别是AB，AC边上的中点， $A D ⊥ B C$ 于点 $D$ ，过点 $E$ 作 $E G / / D F$ 交BC于点 $G$ ，连结GF ，则GF的长为．

查看试题解析
8. 如图，菱形 $A B C D$ 中， $A B = 4, ∠ B = 120 °$ ，将菱形 $A B C D$ 绕点 $A$ 逆时针旋转得到菱形 $A B^{'} C^{'} D^{'}$ ，连接 $C C^{'}$ ，当 $B^{'} C^{'}$ 与 $C D$ 第一次垂直时， $∠ D^{'} C^{'} C$ 的度数为．

查看试题解析
9. 如图，点E，F分别在平行四边形 $A B C D$ 的边 $A B$ ， $C D$ 上，连结 $D E$ ， $E F$ ，点D关于 $E F$ 的对称点G恰好在 $A B$ 的延长线上，连结 $F G$ 交 $B C$ 于点H．若 $\frac{G H}{E G} = \frac{5}{8}$ ， $C F = 1$ ，则 $\frac{F H}{G H} =$ ， $A E =$ ．

查看试题解析
10. 如图，将平行四边形 $A B C D$ 的边 $D C$ 延长线到点 $E$ ，使 $C E = D C$ ，连接 $A E$ ，交 $B C$ 于点 $F$ ．添加一个条件，使四边形 $A B E C$ 是矩形．下列四个条件：① $∠ D A C = ∠ E A C$ ；② $A D = A E$ ；③ $A B = A D$ ；④ $∠ A F C = 2 ∠ A B C$ 中，你认为可选择的是．（填上所有满足条件的序号）

查看试题解析
11. 如图，在菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O， $\frac{A C}{B D} = \frac{5}{3}$ ．线段 $A B$ 与 $A^{'} B^{'}$ 关于过点O的直线l对称，点B的对应点 $B^{'}$ 在线段 $O C$ 上， $A^{'} B^{'}$ 交 $C D$ 于点E，则 $△ B^{'} C E$ 与四边形 $O B^{'} E D$ 的面积比为

查看试题解析
12. 如图，在 $▱ A B C D$ 中， $∠ B = 135 °, A B = \sqrt{2} B C$ ，将 $△ A B C$ 沿对角线 $A C$ 翻折至 $△ E A C, A E$ 与 $C D$ 相交于点 $F$ ，连接 $D E$ ，则 $\frac{D E}{A C}$ 的值为．

查看试题解析

13. 已知：在矩形 $A B C D$ 中， $A C$ 是对角线．求作：菱形 $A E C F$ ，使点 $E ， F$ 分别在边 $A D ， B C$ 上．
作法：如图，①分别以点 $A$ ， $C$ 为圆心，大于 $\frac{1}{2} A C$ 长为半径画弧，两弧在线段 $A C$ 两侧分别交于点 $M ， N$ ；
②作直线 $M N$ 交 $A C$ 于点 $O$ ，与 $A D ， B C$ 分别交于点 $E ， F$ ；
③连接 $A F ， C E$ ．
所以四边形 $A E C F$ 就是所求的菱形．
根据上面设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：连接 $M A ， M C ， N A ， N C$ ．
∵ $M A = M C ， N A = N C$ ，
∴ $M N$ 是 $A C$ 的垂直平分线             （填推理根据）．
∴ $E A = E C$ ．
∴ $∠ E A C = ∠ E C A$ ．
∵四边形 $A B C D$ 是矩形，
∴ $A D ∥ B C$ ，
∴ $∠ E A C = ∠ F C A$ ．
∴ $∠ E C A =$               ．
又 $M N ⊥ A C$ ，
∴ $∠ C O E = ∠ C O F = 90 °$ ．
∴ $∠ C E F = ∠ C F E$ ．
∴ $C F = C E$ ．
∴ $C F = E A$ ．
又∵ $C F ∥ E A$ ，
∴四边形 $A E C F$ 是平行四边形             （填推理根据）．
又∵ $A C ⊥ E F$ ，
∴四边形 $A E C F$ 是菱形             （填推理根据）．

查看试题解析

14. 如图，在平行四边形ABCD中，对角线AC，BD交于点O，点E，F分别为AO，CO的中点，连接EB，BF，FD，DE.

(1)、求证：四边形BFDE是平行四边形.

(2)、若 $∠ A B D = 9 0^{°}$ ， $A B = 2 B O = 4$ ，求线段BE的长.

查看试题解析
15. 小宁同学按如下步骤作四边形 ABCD：①画 $∠ M A N$ ；②以点 A 为圆心，3cm长为半径画弧，分别交 AM， AN 于点 B， D； ③分别以点 B， D，为圆心，3cm长为半径画弧，两弧交于点 C；④连接 BC， DC.

(1)、求证：四边形 ABCD 是菱形.

(2)、连结 BD，若 $B D = 2 c m$ ，求四边形 ABCD 的面积.

查看试题解析
16. 如图， $▱ A B C D$ 中，点 $E$ 是 $A D$ 的中点，连接 $C E$ 并延长交 $B A$ 的延长线于点 $F$ ．

(1)、求证： $A F = A B$ ；

(2)、点 $G$ 是线段 $A F$ 上一点，满足 $∠ F C G = ∠ F C D, C G$ 交 $A D$ 于点 $H$ ．
①求证： $A H \cdot C H = D H \cdot G H$ ；
②若 $A G = 2, F G = 6$ ，求 $G H$ 的长．

查看试题解析

17. 【综合与实践】生活中，我们所见到的地面、墙面、服装面料等，上面的图案常常是由一种或几种形状相同的图形拼接而成的．用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，就是平面图形的镶嵌．

(1)、如图1，在 $▱ A B C D$ 中， $A B = 2$ ， $A D = 3$ ， $∠ B A D = 60 °$ ，图2右侧的阴影部分可以看成是左侧阴影部分沿射线 $A D$ 方向平移而成，其中，平移的距离是______．同理，再进行一次切割平移，可得图3，即图4可以看成由平行四边形经过两次切割平移而成．我们可以用若干个如图4所示的图形，平面镶嵌成如图5的图形，则图5的面积是______

(2)、小明家浴室装修，在墙中央留下了如图6所示的空白，经测量可以按图7所示，全部用边长为1的正三角形瓷砖镶嵌．小明调查后发现：一块边长为1的正三角形瓷砖比一块边长为1的正六边形瓷砖便宜40元；用500元购买正三角形瓷砖与用2500元购买正六边形瓷砖的数量相等．
①请问两种瓷砖每块各多少元？
②小明对比两种瓷砖的价格后发现：用若干块边长为1的正三角形瓷砖和边长为1的正六边形瓷砖一起镶嵌总费用会更少．按小明的想法，将空白处全部镶嵌完，购买瓷砖最少需要______元．

查看试题解析
18. 综合与实践课上，诸葛小组三位同学对含 $60 °$ 角的菱形进行了探究．
【背景】在菱形 $A B C D$ 中， $∠ B = 60 °$ ，作 $∠ P A Q = ∠ B$ ， $A P$ 、 $A Q$ 分别交边 $B C$ 、 $C D$ 于点P、Q．

(1)、【感知】如图1，若点P是边 $B C$ 的中点，小南经过探索发现了线段 $A P$ 与 $A Q$ 之间的数量关系，请你写出这个关系式______．

(2)、【探究】如图2，小阳说“点P为 $B C$ 上任意一点时，（1）中的结论仍然成立”，你同意吗？请说明理由．

(3)、【应用】小宛取出如图3所示的菱形纸片 $A B C D$ ，测得 $∠ A B C = 60 °$ ， $A B = 6$ ，在 $B C$ 边上取一点P，连接 $A P$ ，在菱形内部作 $∠ P A Q = 60 °$ ， $A Q$ 交 $C D$ 于点Q，当 $A P = 2 \sqrt{7}$ 时，请直接写出线段 $D Q$ 的长．

查看试题解析

19. 阅读理解：
如图①，如果四边形ABCD满足AB=AD，CB=CD，∠B=∠D=90°，那么我们把这样的四边形叫做“完美筝形”．

将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状，再展开得到图③，其中CE，CF为折痕，∠BCE=∠ECF=∠FCD，点B′为点B的对应点，点D′为点D的对应点，连接EB′，FD′相交于点O．

简单应用：

(1)、在平行四边形、矩形、菱形、正方形四种图形中，一定为“完美筝形”的是；

(2)、当图③中的∠BCD=120°时，∠AEB′=°；

(3)、当图②中的四边形AECF为菱形时，对应图③中的“完美筝形”有个（包含四边形ABCD）．
拓展提升：

(4)、当图③中的∠BCD=90°时，连接AB′，请探求∠AB′E的度数，并说明理由．

查看试题解析

20. 如图，在平行四边形 $A B C D$ 中， $A B = A C = 9$ ， $B C = 12$ ，点E是 $B C$ 的中点，将 $B E$ 绕点E顺时针旋转得到 $B^{'} E$ ，过点E作 $∠ B E B^{'}$ 的角平分线，角平分线交平行四边形 $A B C D$ 的边 $A B$ 于点P．

(1)、连接 $A E$ ，求证： $△ A B E ≌ △ A C E$ ；

(2)、在旋转过程中，求点 $B^{'}$ 与点D之间的最小距离；

(3)、在旋转过程中，若点 $B^{'}$ 落在 $△ A B C$ 的内部（不包含边界），求 $A P$ 的取值范围；

(4)、已知 $B^{'} E$ 与边 $A B$ 交于H点，若 $∠ E H B = 90 °$ ，直接写出点 $B^{'}$ 到 $A D$ 的距离．

查看试题解析

四边形之平行四边形与菱形-【考前20天】2025年中考数学终极冲刺专题

一、选择题

二、填空题

三、作图题

四、解答题

五、实践探究题

六、阅读理解题

七、综合题