第六章 平行四边形 单元提升检测-2024-2025学年北师大版八年级数学下册
试卷更新日期:2025-05-27 类型:单元试卷
一、选择题(每题3分,共24分)
-
1. 如图,在□ABCD中,对角线AC , BD相交于点O , OE⊥BD交DC的延长线于点E , 连接BE , 若□ABCD的周长为28,△BCE的周长为18,则CE的长是( )
 A、4 B、3 C、2 D、12. 已知,如图,在中,是AD上方任意一点。若的面积为4,的面积为的面积为10,则的面积为( )
A、4 B、3 C、2 D、12. 已知,如图,在中,是AD上方任意一点。若的面积为4,的面积为的面积为10,则的面积为( ) A、2.5 B、2 C、1.5 D、13. 将一个平行四边形纸片进行折叠,第一次折叠经过点A , 使的两边重合,折痕交边CD于点E , 第二次折叠经过点B , 使的两边重合,折痕交边CD于点F , 如图是一种折叠后的效果,当点 , , , 相邻两点间的距离相等时,若=6,则AD的长为( )
A、2.5 B、2 C、1.5 D、13. 将一个平行四边形纸片进行折叠,第一次折叠经过点A , 使的两边重合,折痕交边CD于点E , 第二次折叠经过点B , 使的两边重合,折痕交边CD于点F , 如图是一种折叠后的效果,当点 , , , 相邻两点间的距离相等时,若=6,则AD的长为( ) A、2 B、4 C、2或4 D、2或4或124. 如图,在中,对角线 , , 直线过点 , 连接 , 的周长等于周长的一半,下列说法正确的是( )
A、2 B、4 C、2或4 D、2或4或124. 如图,在中,对角线 , , 直线过点 , 连接 , 的周长等于周长的一半,下列说法正确的是( )①;②;③;④
 A、①② B、①②③ C、②③④ D、③④
A、①② B、①②③ C、②③④ D、③④二、填空题(每题3分,共18分)
-
5. 如图,在Rt△ABC中,∠ABC=90°,D是斜边AC的中点,BE平分∠ABC且BE⊥CE , 连接DE , 若AC=20,BC=12,则DE的长为 .
 6. 如图,是的边上的点,是中点,连接并延长交于点 , 连接与相交于点 , 若 , 则阴影部分的面积为 .
6. 如图,是的边上的点,是中点,连接并延长交于点 , 连接与相交于点 , 若 , 则阴影部分的面积为 . 7. 如图,点O是▱ABCD的对角线交点,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1 , S2分别表示△EOF和△GOH的面积,则S1:S2=.
7. 如图,点O是▱ABCD的对角线交点,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1 , S2分别表示△EOF和△GOH的面积,则S1:S2=.
三、作图题(共8分)
-
8. 如图,在中,是对角线.
 (1)、利用尺规作线段的垂直平分线,垂足为点O,交边于点E,交边于点F(要求:尺规作图并保留作图痕迹,不写作法,标明字母);(2)、试猜想线段与的数量关系,并加以证明.
(1)、利用尺规作线段的垂直平分线,垂足为点O,交边于点E,交边于点F(要求:尺规作图并保留作图痕迹,不写作法,标明字母);(2)、试猜想线段与的数量关系,并加以证明.四、解答题(共6题,共48分)
-
9. 如图,在中,于点E,于点F,连结AF,CE.
 (1)、证明:四边形AECF是平行四边形;(2)、若 , , , 求BD的长.10. 如图,在平面直角坐标系中直线与直线交于点 , 直线与轴交于点 , 与轴交于点 , 过中点作直线轴.
(1)、证明:四边形AECF是平行四边形;(2)、若 , , , 求BD的长.10. 如图,在平面直角坐标系中直线与直线交于点 , 直线与轴交于点 , 与轴交于点 , 过中点作直线轴. (1)、求直线的解析式和的值;(2)、点在直线上,当时,求点坐标;(3)、点是直线上一动点,点是直线上一动点,当以、、、为顶点的四边形是平行四边形时,求点坐标.
(1)、求直线的解析式和的值;(2)、点在直线上,当时,求点坐标;(3)、点是直线上一动点,点是直线上一动点,当以、、、为顶点的四边形是平行四边形时,求点坐标.五、实践探究题(共6分)
-
11. 【教材呈现】如图,这是人教版八年级下册第48页的部分内容.
如图,D , E分别是的边AB与AC的中点.根据画出的图形,
可以猜想:且 .
对此,我们可以用演绎推理给出证明.

 (1)、【结论应用】
(1)、【结论应用】如图1,在四边形ABCD中, , P是对角线BD的中点,M是DC的中点,N是AB的中点.请判断的形状,并说明理由.
(2)、【应用拓展】如图2,在四边形ABCD中, , M是DC的中点,N是AB的中点,连接NM , 延长BC , NM交于点E . 若 , 求的度数.
六、阅读理解题(共8分)
-
12.(1)、【阅读理解】如图1, , 的面积与的面积相等吗?为什么?
 (2)、【类比探究】问题①,如图2,在正方形的右侧作等腰 , , , 连接 , 求的面积.
(2)、【类比探究】问题①,如图2,在正方形的右侧作等腰 , , , 连接 , 求的面积.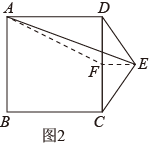 (3)、【拓展应用】问题②,如图3,在正方形的右侧作正方形 , 点B,C,E在同一直线上, , 连接 , , , 直接写出的面积.
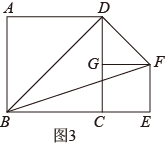
(3)、【拓展应用】问题②,如图3,在正方形的右侧作正方形 , 点B,C,E在同一直线上, , 连接 , , , 直接写出的面积.
七、综合题(共8分)
-
13. 在平行四边形中,平分 , 平分 , 点、在上.
 (1)、如图1,当点、重合时,请你经过推理后直接填空:
(1)、如图1,当点、重合时,请你经过推理后直接填空:①与的数量关系为:;
②与的位置关系为:;
③、、的关系式为: .
(2)、如图2,当点在点左侧时,证明(1)中③的结论仍然成立.(3)、如图3,当点在点右侧时,若 , , 则四边形的面积= .
-
-
-