湘教版(2025)数学七年级下册4.5垂线 同步分层练习
试卷更新日期:2025-05-18 类型:同步测试
一、基础夯实
-
1. 下列图形中,线段的长表示点A到直线距离的是( )A、
 B、
B、 C、
C、 D、
D、 2. 过点作的垂线 , 下列选项中,三角板的放法正确的是( )A、
2. 过点作的垂线 , 下列选项中,三角板的放法正确的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,小华同学的家在点处,他想尽快到达公路边乘车到学校,他选择沿线段去公路边,他的这一选择用到的数学知识是( )
3. 如图,小华同学的家在点处,他想尽快到达公路边乘车到学校,他选择沿线段去公路边,他的这一选择用到的数学知识是( ) A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、经过一点有无数条直线4. 小明同学踩着踏板起跳的跳远训练情况如图所示,点A,B表示两脚的后脚跟,C,D分别在长方形踏板的边缘线上。若AC与BD均垂直于踏板的边缘线,则要想知道他此次跳远成绩,只需测量( )
A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、经过一点有无数条直线4. 小明同学踩着踏板起跳的跳远训练情况如图所示,点A,B表示两脚的后脚跟,C,D分别在长方形踏板的边缘线上。若AC与BD均垂直于踏板的边缘线,则要想知道他此次跳远成绩,只需测量( ) A、线段AC的长度 B、线段AD的长度 C、线段BC的长度 D、线段BD的长度5. 下列图形中,线段的长表示点到直线的距离是( )A、
A、线段AC的长度 B、线段AD的长度 C、线段BC的长度 D、线段BD的长度5. 下列图形中,线段的长表示点到直线的距离是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,三角形ABC中, , 于点D,若 , 则点C到直线AB的距离是( )
6. 如图,三角形ABC中, , 于点D,若 , 则点C到直线AB的距离是( ) A、 B、3 C、4 D、57. 如图,直线相交于点O,于O, , 的度数是( )
A、 B、3 C、4 D、57. 如图,直线相交于点O,于O, , 的度数是( ) A、 B、 C、 D、8. 如图,直线相交于点比大 , 则°.
A、 B、 C、 D、8. 如图,直线相交于点比大 , 则°. 9. 如图,在中,过点C作于点D,M是边上的一个动点,连接 . 若 , 则线段的长的最小值是 .
9. 如图,在中,过点C作于点D,M是边上的一个动点,连接 . 若 , 则线段的长的最小值是 . 10. 如图, , 垂足为 , 为过点的一条直线,若 , 则 .
10. 如图, , 垂足为 , 为过点的一条直线,若 , 则 . 11. 如图,已知 , , 垂足分别为 , F, , 试说明 .
11. 如图,已知 , , 垂足分别为 , F, , 试说明 .
将下面的解答过程补充完整.
证明: , (已知)
又
.
12. 如图,为了解决A,B,C,D四个小区的缺水问题,市政府准备投资修建一个水厂. (1)、不考虑其他因素,请你画图确定水厂 H 的位置,使之与四个小区的距离之和最小.(2)、另外,计划把河流EF 中的水引入水厂H 中,使之到水厂H的距离最短,请你画图确定铺设引水管道的位置,并说明理由.
(1)、不考虑其他因素,请你画图确定水厂 H 的位置,使之与四个小区的距离之和最小.(2)、另外,计划把河流EF 中的水引入水厂H 中,使之到水厂H的距离最短,请你画图确定铺设引水管道的位置,并说明理由.二、能力提升
-
13. 如图,平分平分 , 且 . 有下列结论:①平分;②;③;④ . 其中正确的有( )
 A、1个 B、2个 C、3个 D、4个14. 如图,直线 , 相交于点 , 平分 , 设 , , 下列结论:① , 则;②若 , 则;③若 , 则;④若平分 . 则 , 其中正确的结论是( )
A、1个 B、2个 C、3个 D、4个14. 如图,直线 , 相交于点 , 平分 , 设 , , 下列结论:① , 则;②若 , 则;③若 , 则;④若平分 . 则 , 其中正确的结论是( ) A、①②③④ B、①②④ C、①③④ D、②③④15. 一个箱子静止放在斜坡上,其受力分析如图所示,重力的方向竖直向下,支持力的方向与斜面垂直,摩擦力的方向与斜面平行,若摩擦力与重力方向的夹角的度数为 , 则角的度数为.
A、①②③④ B、①②④ C、①③④ D、②③④15. 一个箱子静止放在斜坡上,其受力分析如图所示,重力的方向竖直向下,支持力的方向与斜面垂直,摩擦力的方向与斜面平行,若摩擦力与重力方向的夹角的度数为 , 则角的度数为. 16. 如图,在的正方形网格中有 , 点均在格点上.
16. 如图,在的正方形网格中有 , 点均在格点上.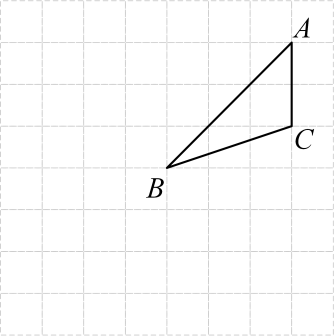 (1)、画出点B到直线的最短路径;(2)、过C点画出的平行线,交于点E;(3)、将向左平移格,再向下平移格后得到 , 画出 .(4)、判断和的数量关系 .17. 现有一块含角的直角三角尺 , 是直角,其顶点在直线上,请解决下列问题:
(1)、画出点B到直线的最短路径;(2)、过C点画出的平行线,交于点E;(3)、将向左平移格,再向下平移格后得到 , 画出 .(4)、判断和的数量关系 .17. 现有一块含角的直角三角尺 , 是直角,其顶点在直线上,请解决下列问题:

 (1)、如图1,请直接写出、的数量关系;(2)、如图2,分别过点、作直线的垂线,垂足分别为、 , 请写出图中分别与、相等的角,并说明理由;(3)、如图3,平分 , 将直角三角尺绕着点旋转,当时,请直接写出与直线所成锐角的度数.
(1)、如图1,请直接写出、的数量关系;(2)、如图2,分别过点、作直线的垂线,垂足分别为、 , 请写出图中分别与、相等的角,并说明理由;(3)、如图3,平分 , 将直角三角尺绕着点旋转,当时,请直接写出与直线所成锐角的度数.三、拓展创新
-
18. 图1是光伏发电场景,其示意图如图2,为吸热塔,在地平线上的点C,D处各安装定日镜(介绍见图3).绕各中心点(A,B)旋转镜面,使过中心点的太阳光线经镜面反射后到达吸热器点O处.A、B处于同一水平高度,已知反射光线与水平线的夹角是 , 镜面与立杆的夹角 , 则太阳光线与水平面夹角;若反射光线与水平线的夹角是时,则 .
 19. 在物理学中,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
19. 在物理学中,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图1,一束光线射到平面镜上,被反射后的光线为 , 则入射光线、反射光线与平面镜所夹的锐角 .
 (1)、【简单应用】
(1)、【简单应用】如图2,有一口井,已知入射光线与水平线的夹角为 , 现放置平面镜 , 可使反射光线正好垂直照射到井底(即射线),与水平线的夹角的度数为 .
(2)、【类比拓展】如图3,有两块平面镜 , 且 , 入射光线经过两次反射,得到反射光线 . 由以上光的反射定律,可知入射角与反射角相等,进而可以推得他们的余角也相等,即: . 在这样的条件下,求证: .
(3)、【尝试探究】两块平面镜 , 且 , 入射光线经过两次反射,得到反射光线 . 如图4,光线与相交于点 , 则的度数是多少?(用含的式子表示)(三角形内角和)