北师大版（2024）数学七下第四章三角形单元测试C卷

试卷更新日期：2025-05-08 类型：单元试卷

进入出卷网下载

一、选择题（本大题共8小题，每小题3分，共24分）

1. 下列各组数中，不能构成三角形三边长的是（）

A、5，12，13 B、1，2，2 C、5，7，12 D、10，11，12

查看试题解析
2. 如图， $A C$ 与 $D B$ 相交于 $E$ ，且 $A E = D E$ ，如果添加一个条件还不能判定 $△ A B E ≌ △ D C E$ ，则添加的这个条件是（）

A、 $A C = D B$ B、 $∠ A = ∠ D$ C、 $∠ B = ∠ C$ D、 $A B = D C$

查看试题解析
3. 数学来源于生活，又服务于生活．以下四幅图中用数学原理解释不正确的是（）

A、图（1）两钉子就能固定木条这样做的道理是利用了两点确定一条直线 B、图（2）人字梯中间一般会设计一根“拉杆”，这样做的道理是利用了三角形的稳定性 C、图（3）体育课堂测量跳远的成绩是利用了垂线段最短 D、图（4）一块三角形模具打碎为三块，只带编号为③的那一块碎片到商店去，就能配一块与原来一样的三角形模具是利用了三角形全等中的判别方法 $SAS$

查看试题解析
4. 三角形一边上的中线把原三角形分成两个（）

A、形状相同的三角形 B、面积相等的三角形 C、直角三角形 D、周长相等的三角形

查看试题解析
5. 如图，已知△CAD≌△CBE，若∠A=30°，∠C=70°，则∠CEB=（）

A、50° B、60° C、70° D、80°

查看试题解析
6. 如图，在 $Rt △ A B C$ 中， $∠ B A C = 90 °$ ， $C D$ 是 $△ A B C$ 的角平分线， $A E ⊥ C D$ 于点 $E$ ，连接 $B E$ ， $A B = 6$ ， $A C = 8$ ， $B C = 10$ ，则 $△ A B E$ 的面积是（）

A、 $\frac{9}{5}$ B、2 C、 $\frac{12}{5}$ D、 $\frac{24}{5}$

查看试题解析
7. 如图，将一边长为 $a$ 的正方形（最中间的小正方形）与四块边长为 $b$ 的正方形（其中 $b > a$ ）拼接在一起，则四边形 $A B C D$ 的面积是（）

A、 $b^{2} + a^{2}$ B、 $b^{2} + {(b - a)}^{2}$ C、 ${(b + a)}^{2}$ D、 $a^{2} + 2 a b$

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $A C = 2 A B$ ， $A D$ 是角平分线， $B F ⊥ A D$ 于点 $F$ ，交 $A C$ 于点 $E$ ，过点 $C$ 作 $C G ⊥ B F$ 于点 $G$ ，下列结论：① $B F = E F$ ；② $A F = C G$ ；③ $A D = C D$ ；④ $∠ A E B = ∠ A D B$ .其中正确的有（）个.

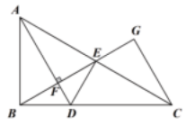A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本题有5小题，每小题3分，共15分）

9. 如图，在 $△ A B C$ 中，E是 $A C$ 的中点，点D在 $B C$ 上，且 $B D = 2 C D$ ， $A D$ 与 $B E$ 交于点F，若 $S_{△ A B F} - S_{四边形 C D F E} = 2$ ，则 $△ A B C$ 的面积为．

查看试题解析
10. 如图，已知 $C D // G H$ ，点 $B$ 在 $G H$ 上，点 $A$ 为平面内一点， $A B$ $⊥ A D$ ，过点 $A$ 作 $A F ⊥ C D ， A E$ 平分 $∠ F A D$ $， A C$ 平分 $∠ F A B$ ，若 $∠ A B C + ∠ G B C = 180^{°} ， ∠ A C B = 4 ∠ F A E$ ，则 $∠ A B G =$ .

查看试题解析
11. 一副三角板按如图方式放置，有下列结论： ① $∠ 1 = ∠ 3$ ； ②若 $B C ∥ A D$ ，则 $∠ 4 = ∠ 3$ ；③若 $∠ 2 = 15^{\circ}$ ，必有 $∠ 4 = 2 ∠ D$ ； ④若 $∠ 2 = 30^{\circ}$ ，则 $A C ∥ D E$ ．其中正确的有.

查看试题解析
12. 如图，已知 $∠ C A B = 30^{\circ} ， ∠ C = 90^{\circ}$ ，过点 $A ， B$ 分别作直线 $A D ， B E$ ，且 $A D ∥ B E$ ， $∠ D A E = 120^{\circ}$ ．给出以下结论：① $∠ 1 + ∠ 2$ $= 90^{\circ}$ ； ② $∠ 2 = ∠ E A B$ ； ③ $A C$ 平分 $∠ D A B$ ．其中正确的结论有

查看试题解析
13. 如图，点O在直线m上，在m的同侧有A，B两点，∠AOB=90°，OA=10cm，OB=8cm，点P以2cm/s的速度从点A出发沿A—O—B路径向终点B运动，同时点Q以1cm/s的速度从点B出发沿B—O—A路径向终点A运动，两点都要到达相应的终点时才能停止运动，分别过点P，Q作PC⊥m于点 C，QD⊥m 于点C，QD⊥m于点D．若△OPC与△OQD全等，则点Q运动的时间是秒．

查看试题解析

三、解答题（本题共7小题，第14题7分，第15题7分，第16题8分，第17题8分，第18题8分，第19题12分，第20题11分，共61分）

14. 如图1是小军制作的燕子风筝，燕子风筝的骨架图如图2所示， $A B = A E$ ， $A C = A D$ ， $∠ B A D = ∠ E A C$ ， $∠ C = 50 °$ ，求 $∠ D$ 的大小．

查看试题解析
15. 如图，分别过点C、B作 $△ A B C$ 的 $B C$ 边上的中线 $A D$ 及其延长线的垂线，垂足分别为E、F．

(1)、求证： $B F = C E$ ；

(2)、若 $△ A C E$ 的面积为6， $△ C E D$ 的面积为2，求 $△ A B F$ 的面积．

查看试题解析
16. 如图，在 $△ A B C$ 中，线段 $A E$ 是 $B C$ 边上的高．

(1)、若 $A D$ 是 $B C$ 边上的中线， $A E = 3 cm$ ， $S_{△ A B C} = 12 {cm}^{2}$ ，求 $B D$ 的长；

(2)、若 $A D$ 是 $∠ B A C$ 的平分线， $∠ B = 40 °$ ， $∠ C = 60 °$ ，求 $∠ D A E$ 的大小．

查看试题解析
17. 如图，两车从路段 $A B$ 的两端同时出发，沿平行路线以相同的速度行驶，相同时间后分别到达C、D两地， $C E ⊥ A B$ ， $D F ⊥ A B$ ，垂足分别为E，F， $C E$ 与 $D F$ 相等吗？为什么？

查看试题解析
18. 某中学八年级（5）班的学生到野外进行数学活动，为了测量一池塘两端A、B之间的距离，同学们设计了如下两种方案：
方案1：如图（1），先在平地上取一个可以直接到达A、B的点C，连接AC并延长AC至点D，连接BC并延长至点E，使DC＝AC，EC＝BC，最后量出DE的距离就是AB的长．
方案2：如图（2），过点B作AB的垂线BF，在BF上取C、D两点，使BC＝CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB间的距离
问：（1）方案1是否可行？并说明理由；
（2）方案2是否可行？并说明理由；
（3）小明说：“在方案2中，并不一定需要BF⊥AB，DE⊥BF，将“BF⊥AB，DE⊥BF”换成条　　也可以．”你认为小明的说法正确吗？如果正确的话，请你把小明所说的条件补上．

查看试题解析
19. 如图①，点G是 $∠ A B C$ 边 $B C$ 上的一点，且 $A G$ 平分 $∠ B A D ， ∠ B A G = ∠ B G A$ ．

(1)、求证： $A D ∥ B C$ ；

(2)、如图②，点E、F分别在图①中射线 $A D 、 B C$ 上运动，且 $∠ A E F = ∠ B$ ，点F在点G左侧，连结 $E G$ ，其它条件不变．求证： $A B ∥ E F$ ；

(3)、如图③，图②中的点F在点G右侧时，设 $∠ B A G = α ， ∠ G E F = β$ ，直接用含 $α ， β$ 的代数式表示 $∠ A G E$ 的度数；

(4)、在图②或图③的射线 $B C$ 下方有一点H，连结 $A H 、 E H$ ，且 $∠ B A H = 2 ∠ H A G ， E H$ 平分 $∠ F E G$ ，若 $∠ B A G = 60 ° ， ∠ F E G = 30 °$ ，直接写出 $∠ A G E + ∠ H$ 的度数．

查看试题解析
20. 在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．

(1)、【感知】
当直线MN绕点C旋转到图①的位置时，易证△ADC≌△CEB（不需要证明），进而得到DE、AD、BE之间的数量关系为．

(2)、【探究】
当直线MN绕点C旋转到图②的位置时，求证：DE＝AD－BE．

(3)、当直线MN绕点C旋转到图③的位置时，直接写出DE、AD、BE之间的数量关系．

查看试题解析

北师大版（2024）数学七下第四章 三角形 单元测试C卷

一、选择题（本大题共8小题，每小题3分，共24分）

二、填空题（本题有5小题，每小题3分，共15分）

三、解答题（本题共7小题，第14题7分，第15题7分，第16题8分，第17题8分，第18题8分，第19题12分，第20题11分，共61分）

北师大版（2024）数学七下第四章三角形单元测试C卷