1-4月之图形基础与三角形—广东省数学2025年中考模拟精选新题速递

试卷更新日期：2025-04-26 类型：二轮复习

进入出卷网下载

一、选择题

1. 如图，是某射箭运动员射箭瞬间的示意图．已知 $A B / / C D, A F / / D E$ ， $∠ 1 = 9 0^{°}, ∠ 2 = 11 0^{°}, ∠ C = 13 5^{°}$ ，则 $∠ C B E$ 的度数是（）

A、 $6 0^{°}$ B、 $6 5^{°}$ C、 $7 0^{°}$ D、 $7 5^{°}$

查看试题解析
2. 如图，一束阳光从天花板和落地窗交界处的点 $P$ 射入，经过地板MN反射到天花板上形成光斑．下午两个不同时刻光线与地板的夹角分别为 $α, β$ ．已知天花板与地面是平行的，且它们之间的距离为3m，当 $α = 4 5^{°}, β = 3 0^{°}$ 时，光斑移动的距离AB为（）

A、3m B、 $(6 \sqrt{3} - 6) m$ C、 $(3 \sqrt{3} - 3) m$ D、6m

查看试题解析
3. 为倡导绿色出行，我市在地铁口设置了共享单车服务。图①是某款共享单车的实物图，图②是其结构示意图支架AB和 CD与地面平行，∠BCD=70°，∠BAC=50°.当∠MAC为多少度时，AM平行于支撑杆BE?（）

A、60 B、70 C、115

查看试题解析
4. 平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等，如图1，一束光线m射到平面镜 $α$ 上，被平面镜 $α$ 反射后的光线为n，则 $∠ 1 = ∠ 2$ . 如图2，一束光线AB先后经平面镜OM、ON反射后，反射光线CD与AB平行. 若 $∠ N C D = 5 8^{°}$ ，则 $∠ M B A$ 的大小为（）

A、 $4 2^{°}$ B、 $3 8^{°}$ C、 $3 2^{°}$ D、 $2 8^{°}$

查看试题解析
5. 图1是某款自动旋转遮阳伞，伞面完全张开时张角呈 $180 °$ ，图2是其侧面示意图．为实现遮阳效果最佳，伞面装有接收器可以根据太阳光线的角度变化，自动调整手柄 $D$ 沿着 $A B$ 移动，以保证太阳光线与 $D F$ 始终垂直，已知支架 $A B$ 长为 $2.5$ 米，且垂直于地面 $B C$ ，某一时刻测得 $B D = 1.7$ 米，悬托架 $A E = D E$ ，点 $E$ 固定在伞面上，当伞面完全张开时，太阳光线与地面的夹角设为 $α$ ，当 $\tan α = \frac{3}{4}$ 时，此时悬托架 $A E$ 的长度为（　　）米．

A、 $0.5$ B、 $0.6$ C、 $0.8$ D、 $0.9$

查看试题解析
6. 若 $△ A B C$ 中， $A B$ 所对的边是 $c$ ， $A C$ 所对的边是 $b$ ，满足 $|\sin A - \frac{\sqrt{3}}{2}| + \sqrt{c - b} = 0$ ，则 $△ A B C$ 是（）

A、等腰三角形 B、直角三角形 C、等边三角形 D、不能确定

查看试题解析
7. 如图， $∠ B A C = ∠ B C D = 90 °$ ， $A C = 2$ ，三角形 $B C D$ 面积始终为2，则 $A D$ 的最大值为（）

A、5 B、 $\sqrt{5}$ C、 $\sqrt{5} + 2$ D、 $\sqrt{5} + 1$

查看试题解析

二、填空题

8. 如图，在 $△ A B C$ 中， $B C = 6$ ， $∠ A B C = 12 0^{°}$ ，点D、E分别在边BC和边AB的延长线上，连接DE，且 $C D = 4$ ， $D E = 3$ ，延长ED交AC于点F，如果点F恰好是AC的中点，那么AB=.

查看试题解析

三、解答题

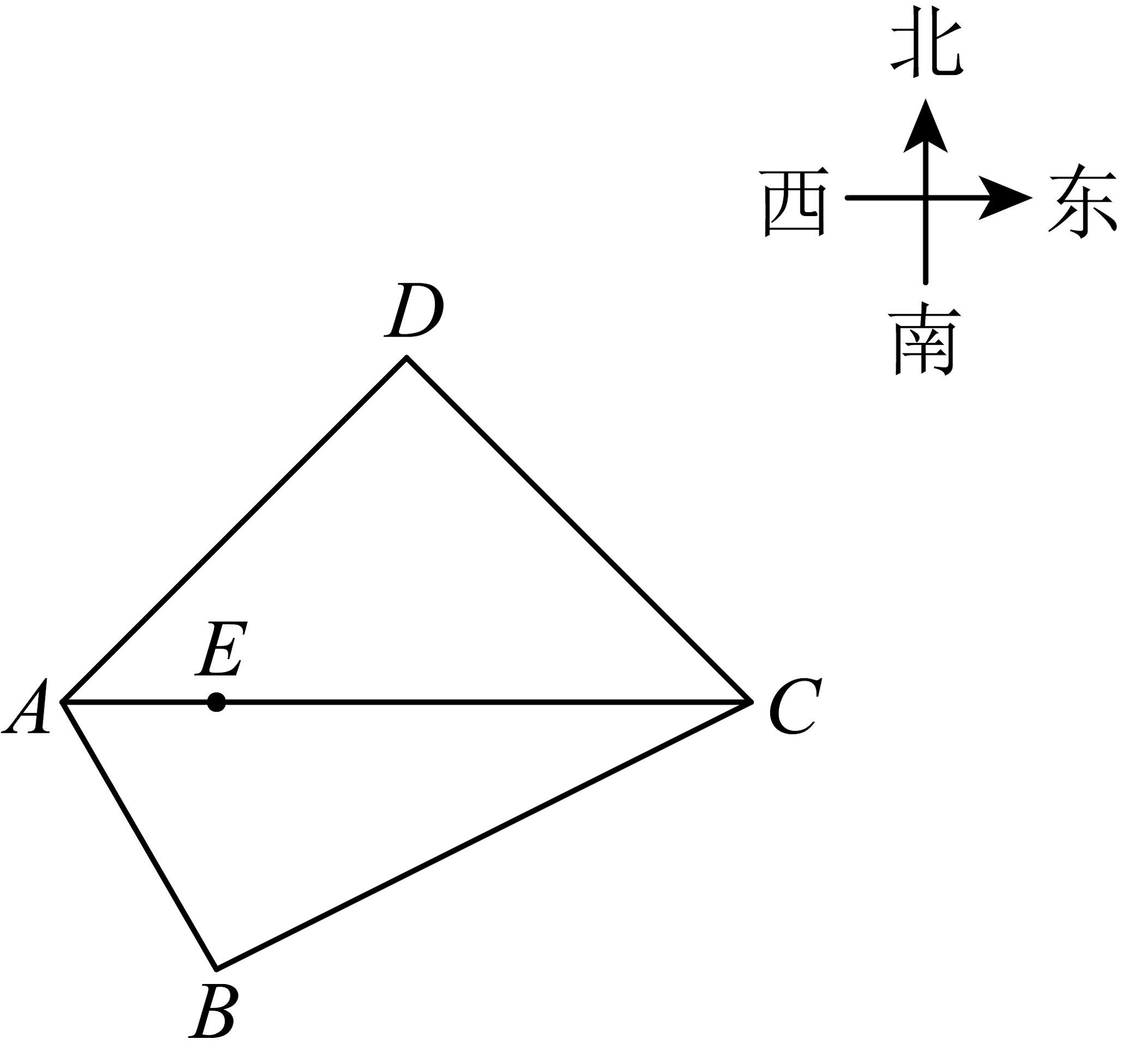9. 在学习了勾股定理后，小品对他家附近的一个公园里的音乐喷泉池产生了测量兴趣，如图，音乐喷泉池为四边形 $A B C D$ ，在 $A C$ 连线上有一地方性标志物 $E$ ，据了解，修建该喷泉池时要求 $E C = 2 \sqrt{3} A E$ ，四边形 $A B C D$ 为人行观赏步道，小品通过仪器测量得到， $A$ 在 $C$ 的正西方， $D$ 在 $A$ 的东北方向，且 $D A = D C$ ， $B$ 在 $E$ 的正南方150米处，恰好又在 $A$ 的南偏东 $30 °$ 方向，由此他脑海里产生了以下数学问题，请你帮他解决一下．（参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ， $\sqrt{5} \approx 2.236$ ， $\sqrt{6} \approx 2.449$ ）

(1)、求 $A$ 、 $C$ 之间的距离（结果保留根号）；

(2)、小品和姐姐同时从 $A$ 点出发，沿着不同的方向到 $C$ 点汇合，其中小品沿着①： $A \to B \to C$ 的方向步行，姐姐沿着② $A \to D \to C$ 的方向步行，通过计算说明哪一条路更近？（结果精确到个位）

查看试题解析
10. 【项目式学习】
问题背景：数学学习中，常常会将新研究的问题转化为以前研究过的熟悉的问题，转化是解决数学问题的一种重要策略．接下来，我们用转化来解决一个有意思的问题．
问题提出：一根绳子，随机分成三段，它们能构成三角形概率是多少？
理解问题：三条线段构成三角形的条件是什么？两边之和大于第三边，两边之差小于第三边．假设绳子长度为1，方程的三段分别是 $x$ ， $y$ ， $z$ ．根据三角形的相关知识，需要符合以下条件： $x + y + z = 1$ ， $x + y > z$ ， $x - y < z$ ， $y - x < z$ 等等．严格来说这是一个多元的不等式组，我们并没学过．但是这里有等式，可以通过“代入消元”的办法得到一些范围．如，将 $x + y = 1 - z$ ，代入 $x + y > z$ ，这就是一个一元一次不等式，可以得到 $z$ 的取值范围是 $0 < z < \frac{1}{2}$ ．
解决问题：

(1)、任务1：
①同理可得， $x$ 的取值范围是 ▲ ， $y$ 的取值范围是 ▲ ．
②如图1，是一个高为1的等边三角形．在等边三角形内任意取一点 $O$ ，连接 $O A$ ， $O B$ ， $O C$ ，把等边三角形分成了三个小三角形，如图2，可以发现， $h_{1}$ ， $h_{2}$ ， $h_{3}$ 与 $h$ 存在数量关系： $h_{1} + h_{2} + h_{3} = h$ ，请给出证明．

(2)、任务2：根据以上构造，设 $x = h_{1}$ ， $y = h_{2}$ ， $z = h_{3}$ ，则 $x + y + z = h_{1} + h_{2} + h_{3} = 1$ ， $x$ ， $y$ ， $z$ 只需要满足以上的不等式即可．请在图3的 $△ A B C$ 中，用阴影部分标记出 $x$ ， $y$ ， $z$ 满足上述条件的区域．（作出必要的说明或标识）

(3)、任务3：阴影部分的面积与 $△ A B C$ 面积之比即为所求的概率，则一根绳子，随机分成三段，能构成三角形的概率是 ▲ ．

查看试题解析
11. 在平面内，先将一个多边形以点 $O$ 为位似中心放大或缩小，使所得多边形与原多边形对应线段的比为 $k$ ，并且原多边形上的任一点 $P$ ，它的对应点 $P^{'}$ 在线段 $O P$ 或其延长线上；接着将所得多边形以点 $O$ 为旋转中心，逆时针旋转一个角度 $θ$ ，记为 $O (k, 逆 θ)$ ，如果是顺时针旋转一个角度 $θ$ ，则记为 $O (k, 顺 θ)$ ，这种经过位似和旋转的图形变换叫做旋转相似变换，其中点 $O$ 叫做旋转相似中心， $k$ 叫做相似比， $θ$ 叫做旋转角．

(1)、填空：
①如图1，将 $△ A B C$ 以点 $A$ 为旋转相似中心，放大为原来的2倍，再逆时针旋转 $60 °$ ，得到 $△ A D E$ ，这个旋转相似变换记为 $A$ （___________，___________）；
②如图2， $△ A B C$ 是边长为 $1cm$ 的等边三角形，将它作旋转相似变换 $A (\sqrt{3}, 逆 90 °)$ ，得到 $△ A D E$ ，则线段 $B D$ 的长为___________ $cm$ ；

(2)、如图3， $△ A B C$ 经过 $B (k_{1}, 逆 α)$ 得到 $△ E B D$ ，又将 $△ A B C$ 经过 $C (k_{2}, 顺 β)$ 得到 $△ F D C$ ，连接 $A E$ ， $A F$ ，求证：四边形 $A F D E$ 是平行四边形．

(3)、如图4，在 $△ A B C$ 中， $∠ A = 150 °$ ， $A B = 6$ ， $A C = 3$ ，若 $△ A B C$ 经过（2）中的变换得到的四边形 $A F D E$ 恰好是正方形时，则 $A E$ 的长为___________．

查看试题解析
12. 综合与探究
【定义】三角形一边上的点将该边分为两条线段，若这两条线段长度的乘积等于这个点与该边所对顶点距离的平方，则称这个点为三角形中该边上的“亮点”．
如图（a），在 $△ A B C$ 中， $D$ 是BC边上一点，连接AD ，若 $A D^{2} = B D \cdot C D$ ，则称点 $D$ 是 $△ A B C$ 中BC边上的“亮点”．

(1)、【概念理解】
如图（b），在Rt△ABC中， $∠ B A C = 9 0^{°}, A D, A E, A F$ 分别是 $△ A B C$ 的高线，角平分线，中线．请判断 $D, E, F$ 三点中哪些是 $△ A B C$ 中BC边上的“亮点”，并说明理由．

(2)、【性质应用】
如图（c），在 $△ A B C$ 中， $∠ B = 4 5^{°}, t a n C = \frac{3}{4}, A C = 10$ ．若 $D$ 是BC边上的“亮点”，求BD的长．

(3)、【拓展提升】
如图（d）， $△ A B C$ 内接于 $⊙ O, D$ 是 $△ A B C$ 中BC边上的“亮点”且 $A D ⊥ A C$ ．若 $s i n B = \frac{1}{3}$ ，求 $\frac{C D}{B D}$ 的值．

查看试题解析
13. 【问题情境】如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ A C B = α$ ，点 $D$ 在边 $B C$ 上 $.$ 将线段 $D B$ 绕点 $D$ 顺时针旋转得到线段 $D E$ （旋转角小于 $180 °$ ），连接 $B E$ ， $C E$ 、以 $C E$ 为底边在其上方作等腰三角形 $F E C$ ，使 $∠ F C E = α$ ，连接 $A F$ ．
【尝试探究】（1）如图 $1$ ，当 $α = 60 °$ 时，易知 $A F = B E$ ；如图 $2$ ，当 $α = 45 °$ 时，则 $A F$ 与 $B E$ 的数量关系为______；
（2）如图 $3$ ，请判断 $∠ E B C$ 与 $∠ F A C$ 的数量关系，并说明理由；
【拓展应用】（3）如图 $4$ ，当 $α = 30 °$ 且点 $B$ ， $E$ 、 $F$ 三点共线时 $.$ 若 $A F = 2 \sqrt{3}$ ， $B D = \frac{1}{5} B C$ ，请求出 $C F$ 的长．

查看试题解析