2024-2025学年浙江省杭州市八年级下学期期中拟试卷 [范围：1-4章]

试卷更新日期：2025-04-05 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 两年前生产1千克甲种药品的成本为80元，随着生产技术的进步，现在生产1千克甲种药品的成本为60元．设甲种药品成本的年平均下降率为 $x$ ，根据题意，下列方程正确的是（）

A、 $80 (1 - x^{2}) = 60$ B、 $80 {(1 - x)}^{2} = 60$ C、 $80 (1 - x) = 60$ D、 $80 (1 - 2 x) = 60$

查看试题解析
2. 若关于x的一元二次方程 $x^{2} + 2 x + m = 0$ 的一个实数根为2，则另一实数根和m的值分别为（）

A、 $- 4$ ， $- 8$ B、 $- 4$ ， 8 C、4， $- 8$ D、4，8

查看试题解析
3. 若a是方程 $2 x^{2} - 4 x - 3 = 5$ 的一个解，则 $2036 - 3 a^{2} + 6 a$ 的值是（）

A、2024 B、 $- 2024$ C、2023 D、 $- 2023$

查看试题解析
4. 若a为方程x²+2x-4＝0的解，则3a²+6a-8的值为（）

A、4 B、2 C、-4 D、-12

查看试题解析
5. 方程 $x^{2} - 4 x = 0$ 的根为( )

A、 $x = 2$ B、 $x = 4$ C、 $x = \pm 2$ D、 $x = 0$ 或 $x = 4$

查看试题解析

二、填空题（每题3分，共18分）

6. 如图，五边形 $A B C D E$ 中， $A E // B C$ ，则 $∠ C + ∠ D + ∠ E$ 的度数为．

查看试题解析
7. 已知a、b是方程x²﹣3x﹣5＝0的两根，则代数式2a³﹣6a²+b²+7b+1的值是．

查看试题解析
8. 如图，在平行四边形ABCD中， $∠ B A D = 6 0^{°} ， A B = 4$ ，对角线AC、BD交于点 $O$ ，经过点 $O$ 的直线交AD于点 $E$ ，且平分 $△ A B D$ 的周长，则 $O E =$ .

查看试题解析

三、解答题（共8题，共72分）

9. 如图是一张长12cm，宽10cm的矩形铁皮，将其剪去两个全等的正方形和两个全等的矩形，剩余部分（阴影部分）可制成底面积是24cm²的有盖的长方体铁盒，求剪去的正方形的边长．

查看试题解析
10. 如图，在▱ABCD中，AB=4cm，AD=7cm，∠ABC的平分线交AD于点E，交CD的延长线于点F，求DF的长.

查看试题解析
11. 如图，用长为22米的篱笆，一面利用墙（墙的最大可用长度为14米），围成中间隔有一道篱笆的长方形花圃ABCD，为了方便出入，在建造篱笆花圃时，在BC上用其他材料做了宽为1米的两扇小门．若花圃的面积刚好为45m² ，求花圃的长与宽．

查看试题解析
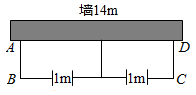12. 如图，用一条长20m的绳子围成矩形 $A B C D$ ，设边 $A B$ 的长为 $x m$ ．

(1)、直接写出 $A D$ 的长；（用含x的代数式表示）

(2)、矩形 $A B C D$ 的面积是否可以是 $60 m^{2}$ ？请给出你的结论，并用所学知识说明理由．

查看试题解析
13. 探索与实践
某中学八年级（1）班小聪同学在学习二次根式后发现一些含根号的式子可以写成另一个式子的平方，如 $3 + 2 \sqrt{2} = {(1 + \sqrt{2})}^{2}$ ，善于开动脑筋思考的小聪进行了以下探索：
设 $a + b \sqrt{2} = {(m + n \sqrt{2})}^{2}$ （其中a ， b ， m ， n均为整数），则有： $a + b \sqrt{2} = m^{2} + 2 n^{2} + 2 m n \sqrt{2}$ ，所以 $a = m^{2} + 2 n^{2}$ ， $b = 2 m n$ ．
这样小聪就找到一种把类似 $a + b \sqrt{2}$ 的式子化成平方式的方法，请你仿照小聪的方法探索并解决下列问题：

(1)、[初步尝试]当a ， b ， m ， n均为正整数时，若 $a + b \sqrt{3} = {(m + n \sqrt{3})}^{2}$ ，用m ， n的式子分别表示a ， b ，得 $a =$ ， $b =$ ；

(2)、[探索实践]利用所探索的结论，找一组正整数a ， b ， m ， n填空： $______+______\sqrt{3} = {(______+______\sqrt{3})}^{2}$ ；

(3)、[拓展应用]若 $a + 4 \sqrt{3} = {(m + n \sqrt{3})}^{2}$ ，且a ， m ， n均为正整数，求a的值．

查看试题解析
14.

(1)、如图1，在四边形 $A D B C$ 中， $A B$ 与 $C D$ 相交于点 $O$ ， $A B = C D$ ， $E$ ， $F$ 分别是 $B C$ ， $A D$ 的中点，连接 $E F$ ，分别交 $D C$ ， $A B$ 于点 $M$ ， $N$ ，判断 $△ O M N$ 的形状，并说明理由；

(2)、如图2，在四边形 $A B C D$ 中， $A B = C D$ ， $E$ ， $F$ 分别是 $A D$ ， $B C$ 的中点，连接 $F E$ 并延长，分别与 $B A$ ， $C D$ 的延长线交于点 $M$ ， $N$ ．求证： $∠ B M E = ∠ C N E$ ．

查看试题解析
15. 如图，在平面直角坐标系中，直线 $y = \frac{1}{2} x - 3$ 与 $x$ 轴、 $y$ 轴分别相交于 $A$ 、 $B$ 两点，点 $C$ 在线段 $O A$ 上，将线段 $C B$ 绕着点 $C$ 逆时针旋转 $90 °$ 得到线段 $C D$ ，此时点 $D$ 恰好落在直线 $A B$ 上．

(1)、求出线段 $A B$ 的长度；

(2)、求出 $B C$ 的函数关系式；

(3)、若点 $E$ 是 $x$ 轴上的一个动点，点 $F$ 是线段 $C B$ 上的点（不与点 $B$ 、 $C$ 重合），是否存在以 $C$ 、 $D$ 、 $E$ 、 $F$ 为顶点的四边形是平行四边形？若存在，求出所有满足条件的 $E$ 点坐标；若不存在，说明理由．

查看试题解析