【培优练】人教版数学八年级下学期 18.2.1 矩形

试卷更新日期：2025-04-03 类型：单元试卷

进入出卷网下载

一、选择题

1. 甲、乙、丙、丁四位同学到木工厂参观时，一木工师傅要他们拿尺子帮助检测一个窗框是否是矩形，他们各自做了如下检测，你认为最有说服力的是（　　）

A、甲量得窗框的一组邻边相等 B、乙量得窗框两组对边分别相等 C、丙量得窗框的对角线长相等 D、丁量得窗框的两组对边分别相等且两条对角线也相等

查看试题解析
2. 我国古代有“不以规矩，不能成方圆”的说法，人们把“规矩”当作几何名词，“规”是圆，“矩”是方，所以现在初中以后就把长方形改为比较专业的名称“矩形”.那么要把 $□ A B C D$ 变成“矩形”，需要增加的条件是（）

A、 $A C = B D$ B、 $A D = B C$ C、 $A B = B C$ D、 $A B = C D$

查看试题解析
3. 矩形具有而平行四边形不一定具有的性质是( )

A、对角线相等 B、对角线互相平分 C、对边相等 D、对角相等

查看试题解析
4. 已知矩形的周长为56，对角线交点到短边的距离比到长边的距离大4，则该矩形的面积为（）

A、45 B、90 C、140 D、180

查看试题解析
5. 如图，矩形 $A B C D$ 中，点 $E$ 在 $B C$ 上，且 $A E$ 平分 $∠ B A C, A E = C E$ ，则 $∠ A E B$ 的度数为（）

A、 $7 5^{∘}$ B、 $6 0^{∘}$ C、 $4 5^{∘}$ D、 $3 0^{∘}$

查看试题解析
6. 如右图，A ， B为 $5 \times 5$ 的正方形网格中的两个格点，称四个顶点都是格点的矩形为格点矩形，则在此图中以A ， B为顶点的格点矩形共可以画出（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，在矩形 $A B C D$ 中， $E$ ， $F$ 分别是 $A D$ ， $C D$ 的中点，连接 $B E$ ， $B F$ ，且 $G$ ， $H$ 分别是 $B E$ ， $B F$ 的中点，已知 $B D = 20$ ，则 $G H$ 的长为( )

A、 $4$
B、 $5$
C、 $8$
D、 $10$

查看试题解析
8. 如图，对折矩形纸片 $A B C D$ ，使 $A D$ 与 $B C$ 重合，得到折痕 $E F$ ，把纸片展平，再一次折叠纸片，使点 $A$ 落在 $E F$ 上，并使折痕经过点 $B$ ，得到折痕 $B M$ ，同时得到线段 $B N$ . 若 $B M$ 与 $E F$ 交点为 $G, M N = 2$ ，则 $G N = ()$

A、1 B、2 C、 $2 \sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
9. 将两个完全相同的矩形 $A B C D$ 和矩形 $E C G F$ 按如图所示的位置摆放，使点 $B$ ， $C$ ， $G$ 在同一条直线上，点 $E$ 在 $C D$ 边上，连结 $A C$ ， $C F$ ， $A F$ ．若 $A B = 12$ ， $B C = 5$ ，则 $△ A C F$ 的面积为（）

A、13 B、26 C、 $\frac{169}{4}$ D、 $\frac{169}{2}$

查看试题解析
10. 如图， $∠ M O N = 90 °$ ，矩形 $A B C D$ 在 $∠ M O N$ 的内部，顶点 $A$ ， $B$ 分别在射线 $O M$ ， $O N$ 上， $A B = 4$ ， $B C = 2$ ，则点 $D$ 到点 $O$ 的最大距离是( )

A、 $2 \sqrt{2} + 2$ B、 $2 \sqrt{2} - 2$ C、 $2 \sqrt{5} - 2$ D、 $\sqrt{2} + 2$

查看试题解析

二、填空题

11. 如图，在长方形ABCD中，AB＝2，BC＝4，对角线AC的垂直平分线分别交AD、AC与E、O ，连接CE ，则CE的长为．

查看试题解析
12. 如图，在 $Rt △ A B C$ 中， $A C = 6 ， B C = 8 ， ∠ C = 90 °$ ，在边 $A B 、 B C 、 A C$ 上分别取点D、E、F使四边形 $D E C F$ 为矩形，则对角线 $E F$ 的长能取到的所有整数值是．

查看试题解析
13. 如图，在直角三角形ABC和直角三角形ABD中， $∠ A C B = ∠ A D B = 90 °$ ， $A B = 10$ ， M是AB的中点，连接MC，MD，CD，若 $C D = 6$ ，则三角形MCD的面积为．

查看试题解析
14. 如图，矩形ABCD中，AD＝6，AB＝8．点E为边DC上的一个动点，△AD'E与△ADE关于直线AE对称，当△CD'E为直角三角形时，DE的长为．

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $A B = 2 ， A D = 6$ ， O为对角线 $A C$ 的中点，点P在 $A D$ 边上，且 $A P = 2$ ，点Q在 $B C$ 边上，连接 $P Q$ 与 $O Q$ ，则 $P Q - O Q$ 的最大值为， $P Q + O Q$ 的最小值为．

查看试题解析

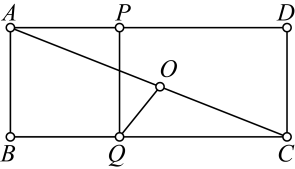
三、解答题

16. 如图，在矩形 $A B C D$ 中，对角线 $A C ， B D$ 相交于点 $O$ ，点 $E ， F$ 分别在边 $A D ， B C$ 上，且 $D E = C F$ ，连结 $O E ， O F$ ．求证： $O E = O F$ ．

查看试题解析
17. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 平分 $∠ B A C$ ， $C E / / A D$ 且 $C E = A D$ ．

(1)、求证：四边形 $A D C E$ 是矩形；

(2)、若 $△ A B C$ 是边长为 $4$ 的等边三角形， $A C$ ， $D E$ 相交于点 $O$ ，在 $C E$ 上截取 $C F = C O$ ，连接 $O F$ ，求四边形 $A O F E$ 的面积．

查看试题解析
18. 如图是以 $A C$ 为对角线的矩形 $A B C D$ 和矩形 $A F C E$ ，且 $C F$ 平分 $∠ A C B$ .

(1)、连接 $D E, B F$ ，求证 $D E = B F$ ；

(2)、尺规作图：作 $∠ C A B$ 的平分线 $A G$ 交 $C F$ 于点 $G$ ，连接 $B F$ .
①求证 $A F = F G$ ；
②若 $A C = 10, A G = 2 \sqrt{10}$ ，求 $B F$ 和 $A B$ 的长.

查看试题解析
19. 如图，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边 $E F$ 交AC于点F．

(1)、求证：四边形ADEF为平行四边形；

(2)、延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．

查看试题解析
20. 如图1，点O为矩形ABCD对角线AC的中点，AB=4，BC=8，点E为BC边上一点，连结EO并延长，交AD于点F．四边形ABEF与四边形A₁B₁EF关于EF所在直线成轴对称，线段FA₁交边BC于点H，连结OH．

(1)、求证： $O H ⊥ E F$ 。

(2)、若 $B E = 1$ ，求 $F D, E H$ 的长。

(3)、如图 2，连结 $O B_{1}$ ，若 $O H = O B_{1}$ ，求 $B E$ 的长。

查看试题解析

21. 【课本再现】

思考：我们知道，矩形的对角线相等，反过来，对角线相等的平行四边形是矩形吗？
可以发现并证明矩形的一个判定定理：对角线相等的平行四边形是矩形．

(1)、【定理证明】
为了证明该定理，小明同学画出了图形

(

如图

(1))

并写出了“已知”和“求证”，请你完成证明过程：
已知：在▱

A B C D

中，对角线

A C

，

B D

相交于点

O

，且

A C = B D

，求证：▱

A B C D

是矩形，

(2)、【知识应用】
如图

(2)

在▱

A B C D

中对角线

A C

和

B D

相交于点

O

，

O A = O B

．

①

求证：▱

A B C D

是矩形；

②

若

A B = 3

，

A D = 4

，

P

是

A D

边上不与

A

和

D

重合的一个动点，过点

P

分别作

A C

和

B D

的垂线，垂足为

E

，

F

，求

P E + P F

的值．

查看试题解析