湘教版（2024）数学七年级下册2.2立方根同步分层练习

试卷更新日期：2025-02-19 类型：同步测试

进入出卷网下载

一、夯实基础

1. 实数﹣27的立方根是（）

A、﹣3 B、±3 C、3 D、﹣ $\frac{1}{3}$

查看试题解析
2. 实数 $\sqrt[3]{- 8}$ 与 $\sqrt[3]{- a}$ 互为倒数，则 $a$ 的值是（）

A、8 B、 $- 8$ C、 $- \frac{1}{8}$ D、 $\frac{1}{8}$

查看试题解析
3. 若 $\sqrt[3]{a} + \sqrt[3]{b} = 0$ ，则 $a$ 与 $b$ 的关系是（）

A、 $a = b = 0$ B、 $a$ 与 $b$ 相等 C、 $a$ 与 $b$ 互为相反数 D、 $a = \frac{1}{b}$

查看试题解析
4. 已知 $2 - 5 n$ 的立方根是 $- 2$ ，则 $n =$ ．

查看试题解析
5. 比较大小：4 $\sqrt[3]{27}$ (填“ > ”“ < ”或“=”)

查看试题解析
6. 计算 $\sqrt[3]{8}$ 和. $\sqrt[3]{- 8},$ ，它们有什么关系? $\sqrt[3]{27}$ 和 $\sqrt[3]{- 27}$ 呢? 你能从中发现什么规律?

查看试题解析
7. 根据下表回答问题：
$x$
16
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
$x^{2}$
256
259.21
262.44
265.69
268.96
272.25
275.56
278.89
282.24
$x^{3}$
4096
4173.281
4251.528
4330.747
4410.944
4492.125
4574.296
4657.463
4741.632

(1)、272.25的平方根是；4251.528的立方根是；

(2)、 $\sqrt{27889} =$ ； $\sqrt{2.6244} =$ ； $\sqrt[3]{4741632} =$ ；

(3)、设 $\sqrt{270}$ 的整数部分为 $a$ ，求 $- 4 a$ 的立方根.

查看试题解析

二、能力提升

8. 若 $a^{2} = 4, b^{3} = 8$ ，则 $2 a - 3 b$ 的值为（）

A、 $- 2$ B、0 C、 $- 2$ 或2 D、 $- 2$ 或 $- 10$

查看试题解析
9. 一个正方体的体积为63，则它的棱长a的取值范围是（）

A、3＜a＜4 B、4＜a＜5 C、7＜a＜8 D、8＜a＜9

查看试题解析
10. 下列计算正确的是（）

A、＝0.5 B、 $\sqrt[3]{- \frac{27}{64}} = \frac{3}{4}$ C、＝1 $\frac{1}{2}$ D、－＝－

查看试题解析
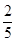11. 下列说法：①实数和数轴上的点是一一对应的；②负数没有立方根；③16的平方根是 $\pm 4$ ，用式子表示是 $\sqrt{16} = \pm 4$ ；④若一个数的绝对值，相反数，算术平方根都是它本身，则这个数是0.其中错误的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
12. 若 $\sqrt{2 x - 50} + | 13 - \frac{1}{3} y | = 0$ ，则 $x + y$ 的立方根是．

查看试题解析
13. 已知一个正数的两个平方根分别是 $2 a + 3$ 和 $6 - 5 a$ ，那么 $8 a + 3$ 的立方根是．

查看试题解析
14. 一个正方体的体积扩大为原来的8倍，它的棱长变为原来的多少倍? 扩大为原来的27倍呢? n倍呢?

查看试题解析
15. 我们知道当 $a + b = 0$ 时， $a^{3} + b^{3} = 0$ 也成立，若将 $a$ 看成 $a^{3}$ 的立方根， $b$ 看成 $b^{3}$ 的立方根，我们能否得出这样的结论：若两个数的立方根互为相反数，则这两个数也互为相反数．

(1)、试举一个例子来判断上述猜测结论是否成立；

(2)、已知 $\sqrt[3]{1 - 2 x} 与 \sqrt[3]{3 x - 5}$ 互为相反数，求 $1 - \sqrt{x}$ 的值．

查看试题解析
16. 阅读材料：
我们知道 $\sqrt{2}$ 是无理数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分，又例如： $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ，即 $2 < \sqrt{5} < 3$ ，所以 $\sqrt{5}$ 的整数部分为2，小数部分为 $\sqrt{5} - 2$ .请根据以上信息，回答下列问题：

(1)、 $\sqrt{34}$ 的整数部分是，小数部分是；

(2)、如果 $\sqrt{11}$ 的整数部分为a ， $7 - \sqrt{7}$ 的整数部分为b ，求 $12 a + 7 b$ 的立方根.

查看试题解析

三、拓展创新

17. 一个正方体木块的体积是 $125 {cm}^{3}$ ，现将它锯成8块同样大小的小正方体木块，其中一个小正方体木块的表面积是多少？

查看试题解析
18. 如图是一种圆柱形升降阻车桩，它的体积为 $22 600 c m^{3},$ 高h等于底面半径r的5.48倍，底面半径r是多少厘米? （π取3.14，结果保留小数点后两位.）

查看试题解析

19. 跟华罗庚学猜数：

据说，我国著名数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：一个数是59319，希望求它的立方根．华罗庚脱口而出：39．邻座的乘客十分惊奇，忙问计算的奥妙．

你知道华罗庚是怎样迅速准确地计算出来的吗？请按照下面的问题试一试：

① $∵ \sqrt[3]{1000} = 10, \sqrt[3]{1000000} = 100$ ，又 $∵ 1000 < 59319 < 1000000$ ，

$∴ 10 < \sqrt[3]{59319} < 100$ ， $∴$ 能确定59319的立方根是个两位数．

②59319的个位数是9，又 $∵ 9^{3} = 729, ∴$ 能确定59319的立方根的个位数是9．

③若划去59319后面的三位319得到数59，而 $\sqrt[3]{27} < \sqrt[3]{59} < \sqrt[3]{64}$ ，则 $3 < \sqrt[3]{59} < 4$ ，可得 $30 < \sqrt[3]{59319} < 40$ ，

由此确定59319的立方根的十位数是3，因此59319的立方根是39．

(1)、现在换一个数50653，按这种方法求立方根，请完成下列填空：

①它的立方根是位数；②它的立方根的个位数字是；③50653的立方根是．

(2)、求175616的立方根．（过程可按题目中的步骤写）

查看试题解析

$x$	16	16.1	16.2	16.3	16.4	16.5	16.6	16.7	16.8
$x^{2}$	256	259.21	262.44	265.69	268.96	272.25	275.56	278.89	282.24
$x^{3}$	4096	4173.281	4251.528	4330.747	4410.944	4492.125	4574.296	4657.463	4741.632

湘教版（2024）数学七年级下册2.2立方根 同步分层练习

一、夯实基础

二、能力提升

三、拓展创新

湘教版（2024）数学七年级下册2.2立方根同步分层练习