北师大版（2024）数学七下第二章 相交线与平行线 单元测试C卷

试卷更新日期：2025-01-20 类型：单元试卷

进入 出卷网 下载

一、选择题（本大题共8小题，每小题3分，共24分）

  • 1. 将一把直尺的一部分和一块三角板按如图所示方式摆放，若∠1比∠2小20°，则∠1的度数为 ( )

    A、20° B、25° C、30° D、35°

    查看试题解析

  • 2. 平面内10条直线把平面分成的部分个数最多是( )
    A、46 B、55 C、56 D、67

    查看试题解析

  • 3.  已知∠α与∠β满足 2∠α+3∠β=180°（∠α≠ 0°,∠β≠0°）, ， 下列式子表示的角：①90°-∠β； ②30∘+32∠α;③∠α+12∠β;④2∠α+∠β中，是∠β的余角的是（   ）
    A、①② B、①③ C、②④ D、③④

    查看试题解析

  • 4. 如图，O是直线AC上一点，OB是一条射线，OD平分∠AOB，OE在∠BOC内，且∠DOE=60°，∠BOE=13∠EOC ， 则下列四个结论中正确的个数有( )

    ①∠BOD=30°；②射线OE平分∠AOC；③图中与∠BOE互余的角有2个；④图中互补的角有6对.

    A、1 B、2 C、3 D、4

    查看试题解析

  • 5. 如图是一款手推车的平面示意图， 其中 AB//CD,∠1= 24∘,∠3=148∘ ，  则 ∠2 的度数为（                ）

    A、56 B、66∘ C、98∘ D、104∘

    查看试题解析

  • 6.  已知 AB//CD ，直线 EF 交 AB 于点 E ，交 CD 于点 F,P 是直线 AB 上一动点，过 P 作直线 EF 的垂线交 CD 于点 Q ，连结 EQ . 若 ∠APQ=∠EQP,∠APQ:∠EFQ=5:4 ，则 ∠AEQ=（ ）

    A、90∘ B、100∘ C、108∘ D、110∘

    查看试题解析

  • 7. 光线从一种介质射向另一种介质时会发生折射．如图，这是一块玻璃的a ， b两面（玻璃上下两个面）的示意图，且a∥b ， 一束光从玻璃a面的C处射向玻璃b面的D处，但从玻璃b面的D处射出时发生了折射，使光线从CD变成了DE ， F为光线CD延长线上一点．已知∠ 1=135° ， ∠2=25° ， 则∠3的度数为（   ）

    A、20° B、25° C、35° D、30°

    查看试题解析

  • 8. 如图，AB//CD ， F为AB上一点，FD//EH ， 且FE平分∠AFG ， 过点F作FG⊥EH于点G ， 且∠AFG=2∠D ． 则下列结论：①∠D=40°；②2∠D+∠EHC=90°；③FD平分∠HFB；④FH平分∠GFD ． 其中正确结论的个数是（ ）

    A、1个 B、2个 C、3 D、4个

    查看试题解析

二、填空题（本题有5小题，每小题3分，共15分）

  • 9.  已知两个角∠α与∠β的两边分别平行，∠α比∠β的3倍少36°，则∠α的度数是.

    查看试题解析

  • 10.  同一平面内∠A和∠B一组边互相平行，另一组边互相垂直，若∠A=m° ， ∠B=n° ， 且m>n ， 则m和n满足的数量关系为 ．

    查看试题解析

  • 11. 如图，点O在直线AB上，从点O引出射线OC，其中射线OD平分∠AOC，射线OE平分∠BOC，下列结论：

    ①∠DOE＝90°；

    ②∠COE与∠AOE互补；

    ③若OC平分∠BOD，别∠AOE＝150°；

    ④∠BOE的余角可表示为12(∠AOE−∠BOE) ．

    其中正确的是  ． （只填序号）

    查看试题解析

  • 12. 如图，等边三角形ABC的边长是2，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接MN，则在点M运动过程中，线段MN长度的最小值是 ．

    查看试题解析

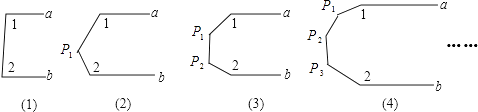
  • 13.

    观察下列图形：已知a∥b，在第一个图中，可得∠1+∠2=180°，则按照以上规律，∠1+∠2+∠P1+…+∠Pn=度．

    查看试题解析

三、解答题（本题共7小题，第14题6分，第15题8分，第16题9分，第17题8分，第18题10分，第19题10分，第20题10分，共61分）

  • 14. 如图， △ABC 中， 点 D 在 BC 边上.

    (1)、 在 AC 边上求作点 E ，  使得 ∠CDE=∠ABC ；（要求：尺规作图，不写作法，保留作图痕迹）
    (2)、在 (1) 的条件下， 若 ∠A=65∘ ，  求 ∠AED 的度数.

    查看试题解析

  • 15. 如图，已知点B、C在线段AD的异侧，连接AB、CD ， 点E、F分别是线段AB、CD上的点，连接CE、BF ， 分别与AD交于点G、H ， 且∠AEG=∠AGE ， ∠C=∠DGC ．

    (1)、求证：AB∥CD；
    (2)、若∠AGE+∠AHF=180° ， 求证：∠B=∠C；
    (3)、在（2）的条件下，若∠BFC=2∠A ， 求∠A的度数．

    查看试题解析

  • 16.

    (1)、已知：如图1 ， 直线AC//BD ， 求证：∠APB=∠PAC+∠PBD；
    (2)、如图2 ， 如果点P在AC与BD之内，线段AB的左侧，其它条件不变，∠APB、∠PAC、∠PBD这三个角之间有怎样的数量关系？并加以证明；
    (3)、如图3 ， 如果点P在AC与BD之外，其他条件不变，请直接写出∠APB、∠PAC、∠PBD这三个角之间有怎样的数量关系．

    查看试题解析

  • 17. 已知 ∠AOB=α（0°<α<30°）,∠AOB 与∠AOC 的和为 60°，∠AOB 与∠AOD 互补.（本题所研究的角均大于 0°小于 180°）
    (1)、如图，当点 B在∠AOC的内部，且点 B，D在OA 的同侧时：

    ①若∠BOC=10°，则α=            °.

    ②若射线 OM 在∠AOD 的内部，且满足∠DOM=2∠AOM，求∠COM 的度数（用含α的式子表示）.

    (2)、直接写出∠COD 所有可能的度数（用含α的式子表示）.

    查看试题解析

  • 18.  直角三角板ABC 的直角顶点C在直线DE 上，CF 平分∠BCD.

    图1 图2

    (1)、在图1中，若∠BCE=40°，求∠ACF 的度数.
    (2)、在图1中，若∠BCE=α，求∠ACF 的度数(用含α的式子表示).
    (3)、将图1中的三角板ABC 绕顶点C旋转至图2的位置，探究：写出∠ACF 与∠BCE 的度数之间的关系，并说明理由.

    查看试题解析

  • 19. 【问题】如图，直线AC与直线AB、CD分别交于点A、点C ， 且AB//CD ， 点Q为直线CD上一定点（C点除外），点P为线段AC上一动点，当点P在线段AC上运动时（端点C除外），∠CPQ+∠CQP与∠BAC有何数量关系？

    【问题探究】甲、乙两位同学对此问题进行了探究，甲同学得出的结论为∠BAC=∠CPQ+∠CQP；乙同学得出的结论为∠BAC+∠CPQ+∠CQP=180°.

    【结论分析】对甲、乙两位同学得出的不同结论，总体评估有以下可能性：①两个结论都正确；②两个结论中只有一个正确；③两个结论都不正确，另有正确结论；④两个结论都不完全正确，另有正确结论；等等.

    【问题解决】在以上分析、评估的基础上，请你就∠CPQ+∠CQP与∠BAC有何数量关系发表自己的看法，并说明理由证明你的结论.（若备用图不够，可自画图）

    查看试题解析

  • 20. 如图，直线PQ//MN ， 点C是PQ、MN之间(不在直线PQ ， MN上)的一个动点．
    (1)、若∠1与∠2都是锐角，如图1 ， 求证：∠C=∠1+∠2 ．
    (2)、把一块三角尺(∠A=30°,∠C=90°)按如图2放置，点D ， E ， F是三角尺的边与平行线的交点，若∠AEN=∠A ， 求∠BDF的度数；
    (3)、将图2中的三角尺进行适当转动，如图3 ， 直角顶点C始终在两条平行线之间，点G在线段CD上，连接EG ， 且有∠CEG=∠CEM ， 有∠GEN∠BDF的值不变，求出其不变的值．

    查看试题解析