北师大版（2024）数学七下第二章 相交线与平行线 单元测试B卷
试卷更新日期：2025-01-20 类型：单元试卷
一、选择题（本大题共8小题，每小题3分，共24分）
-
1. 若一个角的余角比这个角大40°，则这个角的补角的度数为 ( )A、25° B、115° C、145° D、155°2. 如图 ，中 ， ，以点A为圆心 ，适当长为半径画弧 ，交AB于点E ，交AC于点F ；再分别以点E ，F为圆心 ，大于 的长为半径画弧 ，两弧（所在圆的半径相等）在∠BAC的内部相交于点P ；画射线AP ，与BC相交于点D ，则∠ADC的大小为 ( )
A、60° B、65° C、70° D、80°3. 如图 ，直线a∥b矩形ABCD的顶点A在直线b上 ，若 ∠2=41° ，则∠1的度数为 ( )
A、41 B、51 C、49 D、594. 一次数学实践活动中，小鹏将一条对边互相平行的纸带沿折叠如图 ， 若 ， ， 则为( )
A、 B、 C、 D、5. 如图所示，将长方形沿直线折叠，使点C落在点处，交于E ， ， 则的度数为( )
A、 B、 C、 D、6. 如图所示，不能推出a∥b的条件是( )
A、∠1=∠3 B、∠2=∠4 C、∠2=∠3 D、∠2+∠3=180°7. 如图，C，D在线段BE上，下列四个说法：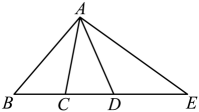
①直线上以B，C，D，E为端点的线段共有6条；②图中有3对互为补角的角；③若 ， 则以A为顶点的所有小于平角的角的度数和为370°；④若BC=4，CD=3，DE=5，点F是线段BE上任意一点（包含端点），则点F到点B，C，D，E的距离之和的最小值为15，最大值为23．
其中正确说法的个数是（ ）
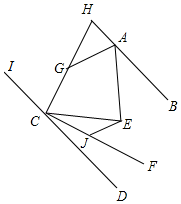
A、1个 B、2个 C、3个 D、4个8. 如图，AB∥CD ， CF平分∠ECD ， HC⊥CF交直线AB于H ， AG平分∠HAE交HC于G ， EJ∥AG交CF于J ， ∠AEC＝80°，则下列结论正确的有（ ）个．①∠BAE+∠ECD＝80°；②CG平分∠ICE；③∠AGC＝140°；④∠EJC﹣∠AGH＝90°．
A、1 B、2 C、3 D、4二、填空题（本题有5小题，每小题3分，共15分）
-
9. 如果∠1 与∠2 互余，∠1 与∠3 互补，∠2 与∠3的和等于周角的 ， 那么∠2 的度数为°.10. 如图，∠AOC与∠BOD都是直角，且∠AOB：∠AOD=2：7，则∠COD=°.
11. 如图，在△ABC中，∠ABC与∠ACB的平分线交于点O，过点O作DE//BC，分别交AB，AC于点D，E，若AB=4，AC=3，则△ADE的周长是 ．
12. 如图，点是量角器的中心点，射线经过刻度线 ． 若 ． 射线、分别经过刻度线和 ， 在刻度线的右侧．下列结论：①；②若与互补，则射线经过刻度线；③若 ， 则图中共有6对角互为余角．其中正确的是（填序号）．
13. 图1是一盏可折叠台灯。图2，图3是其平面示意图，固定底座OA⊥OM于点O，支架BA与CB分别可绕点A和B旋转，台灯灯罩可绕点C旋转调节光线角度，台灯最外侧光线CE，CD组成的∠ECD始终保持不变。如图2，调节台灯使光线CD//BA，CE//OM，此时∠BAO=158°，则∠ECD=.现继续调节图2中的支架CB与灯罩，发现当最外侧光线CE与水平方向的夹角∠CQM=29°，且∠ECD的角平分线CP与CB垂直时，光线最适合阅读(如图3)，则此时∠ABC=.
三、解答题（本题共7小题，第14题6分，第15题6分，第16题6分，第17题10分，第18题9分，第19题12分，第20题12分，共61分）
-
14. 如图，∠A=78°，∠1=78°，∠2=102°.图中有哪些直线互相平行?证明你的判断.
15. 如图， ， ， 试说明的理由．
16. 如图，已知 ， 与相交于点E，若 ， ， 求证： ．
证明：∵（已知），
∴①_________（两直线平行，同旁内角互补），
又∵（已知），
∴（②________）；
∴③____________（同位角相等，两直线平行）．
∴④__________（两直线平行，同位角相等），
∵（已知），
∴（⑤___________________），
∵（已知），
∴（等量代换）．
17. 如图， 是 内的一点. 按下列要求画图， 并回答问题.
(1)、 过点 画直线 ， 交直线 于点 .(2)、 过点 画直线 ， 交直线 于点 .(3)、 分别量出 的度数， 你有什么发现？18. 如图①，点O在直线AB 上，作射线 OC， 0°<∠AOC <90°， OM 平分∠BOC，点 D 在平面内，∠AOC与∠BOD互余。
(1)、如图②，当 D 在∠BOC 内部时，若∠AOC=50°，求∠DOM的度数。(2)、设∠AOC=x°，用含x的代数式表示∠DOM的度数。19.
(1)、【学科融合】光在反射时，光束的路径可用图①来表示，叫做入射光线，叫做反射光线，从入射点O引出的一条垂直于镜面的射线叫做法线．与的夹角叫做入射角，与的夹角叫做反射角．根据科学实验可得 ． 则图①中与的数量关系是 ．
(2)、【数学思考】生活中我们可以运用“激光”和两块相交的平面镜进行测距．如图②，一束“激光”射到平面镜上，被反射到平面镜上，又被平面镜反射后得到反射光线 ．
猜想：当满足什么条件时，任何射到平面镜上的光线经过平面镜和的两次反射后，入射光线与反射光线总是平行的．请你根据所学过的知识及新知探究的结论说明理由．
(3)、【知识应用】人们发明了一种曲面的反射光罩，使汽车灯泡在点O处发出的光线反射后都能平行射出，在如图③所示的截面内，已知入射光线的反射光线为 ， ． 若一入射光线（点D是入射光线与反光罩的交点）经反光罩反射后沿射出，且 ， 请直接写出的度数．
20.
(1)、【发现】如图 ， 直线 ， 被直线所截，平分 ， 平分若 ， ， 试判断与平行吗？并说明理由；(2)、【探究】如图 ， 若直线 ， 点在直线 ， 之间，点 ， 分别在直线 ， 上， ， 是上一点，且平分若 ， 则的度数为；(3)、【延伸】若直线 ， 点 ， 分别在直线 ， 上，点在直线 ， 之间，且在直线的左侧，是折线上的一个动点，保持不变，移动点 ， 使平分或平分设 ， ， 请直接写出与之间的数量关系．