三元平方公式—人教版数学八（上）知识点训练

试卷更新日期：2024-11-24 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知 $\frac{1}{2} a^{2} + \frac{1}{2} b^{2} + \frac{1}{2} c^{2} = 2 - a b - b c - ac$ ，则a+b+c的值是（）

A、2 B、4 C、±4 D、±2

查看试题解析
2. 已知 $a ， b ， c$ 是三角形的三边，且满足 ${(a + b + c)}^{2} = 3 a^{2} + 3 b^{2} + 3 c^{2}$ 则 $△ A B C$ 的形状为（）

A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形

查看试题解析

二、填空题

3. 计算： ${(a - b + 2 c)}^{2} =$ ．

查看试题解析
4. 计算： ${(2 a - b + 3 c)}^{2} =$ ．

查看试题解析

三、解答题

5. 计算：（a+b+c）²

查看试题解析
6. 已知 $a^{2} + b^{2} + c^{2} = 20$ ， $a b + a c + b c = 8$ ，求 $(a + b + c)^{2}$ 的值．

查看试题解析
7. 设实数a，b，c满足a²+b²+c²=1．若a+b+c=0，求ab+bc+ca的值；

查看试题解析
8. 已知 $a + b + c = 6, a^{2} + b^{2} + c^{2} = 14, a^{3} + b^{3} + c^{3} = 36$ ．

(1)、求abc的值；

(2)、 $a^{4} + b^{4} + c^{4}$ 的值．

查看试题解析
9. 要说明(a+b+c)²=a²+b²+c²+2ab+2ac+2bc成立，三位同学分别提供了一种思路，请根据他们的思路写出推理过程.

(1)、小刚说：可以根据乘方的意义来说明等式成立；

(2)、小王说：可以将其转化为两数和的平方来说明等式成立；

(3)、小丽说：可以构造图形，通过计算面积来说明等式成立；

查看试题解析
10. 阅读下面的解题过程．利用乘法公式计算：
⑴(a-b+1)(a+b-1)；
⑵(a+b+c)² ．
解：(1)原式=[a-(b-1)][a+(b-1)]
=a²-(b-1)²
=a²-(b²-2b+1)
=a²-b²+2b-1．
⑵原式=[(a+b)+c]²
=(a+b)²+2(a+b)·c+c²
=a²+2ab+b²+2ac+2bc+c² ．
请根据上述解题思想，利用乘法公式计算下列各题：

(1)、(x-2y+1)(x-2y-1)．

(2)、(2a-3b-c)² ．

查看试题解析
11. 如图，将几个小正方形与小长方形拼成一个边长为(a+b+c)的正方形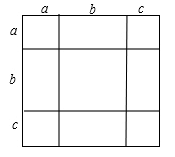

(1)、若用不同的方法计算这个边长为(a+b+c)的正方形面积，就可以得到一个等式，这个等式可以为 .(只要写出一个即可)

(2)、请利用(1)中的等式解答下列问题：
①若三个实数a，b，c满足a+b+c=11，ab+bc+ac=38，求a²+b²+c²的值

②若三个实数x，y，z满足2^x×4^y÷8^z= $\frac{1}{4}$ ，x²+4y²+9z²=44，求2xy-3xz-6yz的值

查看试题解析
12. “以形释数”是利用数形结合思想证明代数问题的一种体现，做整式的乘法运算时利用几何直观的方法获取结论，在解决整式运算问题时经常运用．
例1：如图1，可得等式： $a (b + c) = a b + a c$ ；
例2：由图2，可得等式： $(a + 2 b) (a + b) = a^{2} + 3 a b + 2 b^{2}$ ．

(1)、如图3，将几个面积不等的小正方形与小长方形拼成一个边长为 $a + b + c$ 的正方形，从中你发现的结论用等式表示为______；

(2)、利用（1）中所得到的结论，解决下面的问题：已知 $a + b + c = 10$ ， $a^{2} + b^{2} + c^{2} = 36$ ．求 $a b + b c + a c$ 的值．

(3)、如图4，拼成 $A M G N$ 为大长方形，记长方形 $A B C D$ 的面积与长方形 $E F G H$ 的面积差为S．设 $C D = x$ ，若S的值与 $C D$ 无关，求a与b之间的数量关系．

查看试题解析
13. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式.以图①中的正方形ABCD为例：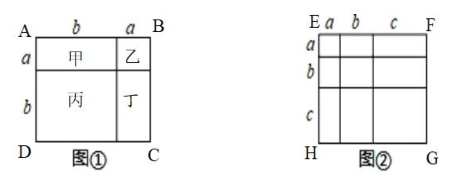
探究：如图①，用含a，b的式子完成以下题目中的（2）和（3）：（1）正方形ABCD的边长为 $a + b$ ，因为正方形的面积等于正方形边长的平方，所以正方形ABCD的面积可以表示为 ${(a + b)}^{2}$ .

(1)、仔细观察图①，正方形ABCD被分割成甲、乙、丙、丁四部分，甲部分的面积为ab，乙部分的面积为 $a^{2}$ ，丙部分的面积为，丁部分的面积为.将这四部分的面积相加就可以得到正方形ABCD的面积为：.

(2)、以上（1）和（2）的探究过程，都表示出了正方形ABCD的面积，从而得到两个数和的平方公式： ${(a + b)}^{2} =$ .

(3)、根据探究的过程，用含有a，b，c的式子表示出由图②中的正方形EFGH可以得到的数学等式：；

(4)、若 $a + b + c = 6$ ， $a^{2} + b^{2} + c^{2} = 14$ ，求 $a b + a c + b c$ 的值；

查看试题解析