整式的混合运算—人教版数学八（上）知识点训练

试卷更新日期：2024-11-24 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 下列计算正确的是（）

A、a²+a³＝2a⁵ B、a²•a³＝a⁶ C、（a²）³＝a⁵ D、a（a+1）＝a²+a

查看试题解析
2. 已知 $a - b = 4$ ， $a b + c^{2} + 4 = 0$ ，则 $a + b =$ ( )

A、 $4$ B、 $0$ C、 $2$ D、 $- 2$

查看试题解析
3. 若（2x﹣y）²+M＝4x²+y² ，则整式M为（　　）

A、﹣4xy B、2xy C、﹣2xy D、4xy

查看试题解析
4. 已知2a²﹣a﹣3＝0，则（2a+3）（2a﹣3）+（2a﹣1）²的值是（　　）

A、6 B、﹣5 C、﹣3 D、4

查看试题解析
5. 定义三角表示3abc ，方框表示xz＋wy ，则×的结果为( )

A、72m²n－45mn² B、72m²n＋45mn² C、24m²n－15mn² D、24m²n＋15mn²

查看试题解析
6. 如图，7张全等的小长方形纸片(既不重叠也无空隙)放置于矩形ABCD中，设小长方形的长为a，宽为b(a>b)，若要求出两块黑色阴影部分的周长和，则只要测出下面哪个数据（）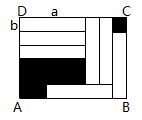

A、a B、b C、a+b D、a-b

查看试题解析
7. 如图，将两张边长分别为 $a$ 和 $b (a > b)$ 的正方形纸片按图 1，图 2 两种方式放置长方形内 (图 1，图 2 中两张正方形纸片均有部分重叠)，未被这两张正方形纸片覆盖的部分用阴影部分表示. 设图 1 中阴影部分面积为 $S_{1}$ ，图 2 中阴影部分面积为 $S_{2}$ . 当 $A B - A D = 3$ 时， $S_{1} - S_{2}$ 的值为 ( )

A、 $3 a$ B、 $3 a - 3 b$ C、 $- 3 b$ D、 $3 b$

查看试题解析
8. 已知 $x^{2} + 2 y - 1 = 0,$ 则 $3 (x^{2} + 2 x y) - （ x^{2} + 6 x y ） + 4 y$ 的值为.

查看试题解析
9. 若方程组 $\{\begin{matrix} 2 x + y = b \\ x - b y = a \end{matrix}$ 的解是 $\{\begin{matrix} x = 1 \\ y = 1 \end{matrix}$ ，则 ${(a + b)}^{2} - (a - b) (a + b) =$ ．

查看试题解析
10. 已知 $| x - y + 1 |$ 与 $x^{2} + 8 x + 16$ 互为相反数，则 $x^{2} + 2 x y + y^{2}$ 的值是.

查看试题解析
11. 先化简，再求值：

(1)、 $2 (\frac{1}{2} x^{2} - 3 x y - y^{2}) - (2 x^{2} - 7 x y - 2 y^{2}),$ 其中 $x = 3, y = - \frac{2}{3} .$

(2)、 $(2 x^{2} + x) - [4 x^{2} - (3 x^{2} - x)],$ 其中x= $- \frac{5}{3} .$

(3)、 $(x - y)^{3} - 4 (x - y)^{2} + 3 (x - y) + 6 （ x -$ $y ）^{2} + (x - y)^{2} - 7 (x - y)^{3} - 5,$ 其中x- $y = \frac{1}{3} .$

查看试题解析
12. 先化简，再求值：已知 $A = 3 x^{2} - 5 x y + y^{2}$ ， $B = 4 x^{2} - 3 y^{2} + 2 y x$ ，求 $- B + 2 A$ 的值，其中 $x$ ， $y$ 满足 $| x + \frac{1}{2} | + (y - 2)^{2} = 0$

查看试题解析
13. “以形释数”是利用数形结合思想证明代数问题的一种体现，做整式的乘法运算时利用几何直观的方法获取结论，在解决整式运算问题时经常运用．
例1：如图1，可得等式： $a (b + c) = a b + a c$ ；
例2：由图2，可得等式： $(a + 2 b) (a + b) = a^{2} + 3 a b + 2 b^{2}$ ．

(1)、如图3，将几个面积不等的小正方形与小长方形拼成一个边长为 $a + b + c$ 的正方形，从中你发现的结论用等式表示为______；

(2)、利用（1）中所得到的结论，解决下面的问题：已知 $a + b + c = 10$ ， $a^{2} + b^{2} + c^{2} = 36$ ．求 $a b + b c + a c$ 的值．

(3)、如图4，拼成 $A M G N$ 为大长方形，记长方形 $A B C D$ 的面积与长方形 $E F G H$ 的面积差为S．设 $C D = x$ ，若S的值与 $C D$ 无关，求a与b之间的数量关系．

查看试题解析

二、能力提升

14. 如图，有三张边长分别为a，b，c的正方形纸片A，B，C，将三张纸片按图1，图2两种不同方式放置于同一长方形中．记图1中阴影部分周长为 $l_{1}$ ，面积为 $S_{1}$ ；图2中阴影部分周长为 $l_{2}$ ，面积为 $S_{2}$ ，若 ${(\frac{l_{2} - l_{1}}{2})}^{2} = 3 (S_{2} - S_{1})$ ，则b与c满足的关系为（）

A、 $3 b = 5 c$ B、 $b = 2 c$ C、 $3 b = 7 c$ D、 $6 b = 7 c$

查看试题解析
15. 关于x的二次三项式 $M = x^{2} + a x + b$ （a，b均为非零常数），关于x的三次三项式 $N = 2 x^{3} - 4 x^{2} + 10 = c {(x - 1)}^{3} + d {(x - 1)}^{2} + e (x - 1) + f$ （其中c，d，e，f均为非零常数），下列说法中正确的个数有（）
①当 $x = - 1$ 时， $N = 4$ ；
②当 $M + N$ 为关于x的三次三项式时，则 $b = - 10$ ；
③当多项式M与N的乘积中不含 $x^{4}$ 项时，则 $a = 2$ ；
④ $e + f = 6$ ；

A、1个 B、2个 C、3个 D、4个

查看试题解析
16. 计算 $(1 - \frac{1}{2} - \frac{1}{3} - \frac{1}{4} - \frac{1}{5}) (\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6}) - (1 - \frac{1}{2} - \frac{1}{3} - \frac{1}{4} - \frac{1}{5} - \frac{1}{6}) (\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5}) =$ ．

查看试题解析
17. 已知 $a = \frac{1}{3} m + 2015$ ， $b = \frac{1}{3} m + 2016$ ， $c = \frac{1}{3} m + 2017$ ，求 $a^{2} + b^{2} + c^{2} - a b - b c - a c$ 的值．

查看试题解析
18. 观察下列等式，回答问题．
$(x - 1) (x + 1) = x^{2} - 1$ ；
$(x - 1) (x^{2} + x + 1) = x^{3} - 1$ ；
$(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ；
$(x - 1) (x^{4} + x^{3} + x^{2} + x + 1) = x^{5} - 1$ ；

(1)、试求 $2^{6} + 2^{5} + 2^{4} + 2^{3} + 2^{2} + 2 + 1$ 的值；

(2)、判断 $2^{2008} + 2^{2007} + 2^{2006} + \cdot \cdot \cdot + 2^{2} + 2 + 1$ 的值的个位数字是几？

查看试题解析
19. 小戴同学通过计算下列两位数的乘积，发现结果也存在一定的规律，请你补充小戴同学的探究过程：
$38 \times 32 = 1216$ ， $43 \times 47 = 2021$ ， $54 \times 56 = 3024$ ， $65 \times 65 = 4225 \dots \dots$

(1)、利用发现的规律计算 $71 \times 79 =$ ．

(2)、根据发现，若设一个两位数的十位上的数字为 $m$ ，个位上的数字为 $n$ ，则另一个两位数的个位上的数字为；
用含 $m$ 、 $n$ 的等式表示以上两位数相乘的规律；

(3)、请用所学知识证明②中的规律．

查看试题解析
20. 【阅读材料】“数形结合”是一种非常重要的数学思想方法．比如：在学习“整式的乘法”时，我们通过构造几何图形，用“等积法”直观地推导出了完全平方和公式： ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ （如图1）．利用“数形结合”的思想方法，可以从代数角度解决图形问题，也可以用图形关系解决代数问题．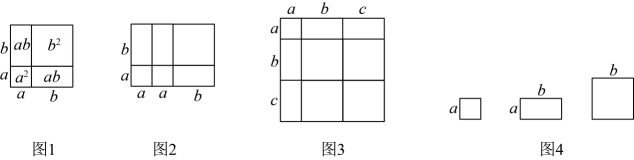
【方法应用】根据以上材料提供的方法，完成下列问题：

(1)、由图2可得等式：；由图3可得等式：；

(2)、利用图3得到的结论，解决问题：若 $a + b + c = 15$ ， $a b + a c + b c = 35$ ，则 $a^{2} + b^{2} + c^{2} =$ ；

(3)、如图4，若用其中 $x$ 张边长为 $a$ 的正方形， $y$ 张边长为 $b$ 的正方形， $z$ 张边长分别为a、b的长方形纸片拼出一个面积为 $(2 a + b) (a + 2 b)$ 长方形（无空隙、无重叠地拼接），则 $x + y + z =$ ．

查看试题解析

三、拓展创新

21. “铺地锦”是我国明朝《算法统宗》里介绍的一种乘法运算方法，可将多位数乘法运算转化为一位数乘法和简单的加法运算．小明受其启发，设计了如图1所示的“表格算法”，图1表示 $142 \times 23$ ，运算结果为3266．图2表示一个三位数与一个两位数相乘，表格中部分数据被墨迹覆盖，根据图2中现有数据进行推断，正确的是（）

A、“15”左边的数是12 B、“15”右边的“ $□$ ”表示5 C、运算结果小于6000 D、运算结果可以表示为 $3100 a + 775$

查看试题解析
22. 有依次排列的两个整式 $A = x^{2} - 1$ ， $B = x^{2} + x$ ，用后一个整式 $B$ 与前一个整式 $A$ 作差后得到新的整式记为 $C_{1}$ ，用整式 $C_{1}$ 与前一个整式 $B$ 作差后得到新的整式 $C_{2}$ ，用整式 $C_{2}$ 与前一个整式 $C_{1}$ 作差后得到新的整式 $C_{3}$ ，依次进行作差的操作得到新的整式．下列说法：①当 $x = a$ 时， $C_{5} = {(a + 1)}^{2}$ ；②当 $C_{9} \times C_{2} = 0$ 时， $A \times B = 0$ ；③ $\frac{C_{2024}}{C_{2023}} = \frac{C_{2021}}{C_{2023}} + 2$ 正确的说法有（）个

A、4 B、3 C、2 D、1

查看试题解析
23. 将 $x - y \div z \times m + n$ （所有字母均不为0）中的任意两个字母对调位置，称为“对调操作”．例如：“ $x$ 、 $y$ 对调操作”的结果为 $y - x \div z \times m + n$ ，且“ $x$ 、 $y$ 对调操作”和“ $y$ 、 $x$ 对调操作”是同一种“对调操作”．
下列说法：
①只有“ $x$ 、 $n$ 对调操作”的结果与原式相等；
②若“ $x$ 、 $y$ 对调操作”与“ $n$ 、 $y$ 对调操作”的结果相等，则 $x = n$ 或 $m + z = 0$ ；
③若 $y = m = z$ ，则所有的“对调操作”共有5种不同运算结果．
其中正确的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
24. 阅读材料：
我们定义：如果两个实数的差等于这两个实数的商，那么这两个实数就叫做“差商等数对”．即：如果 $a - b = a \div b$ ，那么α与b就叫做“差商等数对”，记为 $(a ， b)$ ．例如： $4 - 2 = 4 \div 2$ ； $\frac{9}{2} - 3 = \frac{9}{2} \div 3$ ；则称数对 $(4 ， 2)$ ， $(\frac{9}{2} ， 3)$ 是“差商等数对”．
根据上述材料，解决下列问题：

(1)、下列数对中，“差商等数对”是（填序号）；
① $(- 8.1 ， - 9)$ ② $(\frac{1}{2} ， \frac{1}{2})$ ③ $(- \frac{1}{2} ， - 1)$

(2)、如果 $(a ， 2)$ 是“差商等数对”，请求出a的值；

(3)、在（2）的条件下，先化简再求值： $[(4 a^{2} b - 2 a b^{2} - b^{3}) \div b - (2 a + b) (2 a - b)] \div \frac{2}{3} b$ ．

查看试题解析