完全平方公式—人教版数学八（上）知识点训练

试卷更新日期：2024-11-24 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 若 $(a + b)^{2} = 49$ ， $a b = 12$ ，则 $a^{2} + b^{2}$ 的值为（）

A、 $20$ B、 $25$ C、 $30$ D、 $35$

查看试题解析
2. 已知 $a + \frac{1}{a} = 4$ ，则 $a^{2} + \frac{1}{a^{2}} =$ （）

A、12 B、14 C、16 D、18

查看试题解析
3. 已知M是含字母 $x$ 的单项式，要使多项式 $9 x^{2} + M + 1$ 是某一个多项式的平方，则M等于（）

A、 $6 x$ B、 $\pm 6 x$ C、 $3 x$ D、 $- 6 x$

查看试题解析
4. 我们可以利用图形中的面积关系来解释很多代数恒等式．给出以下4组图形及相应的代数恒等式：
① ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$     ② ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$
③ $(a + b) (a - b) = a^{2} - b^{2}$      ④ ${(a - b)}^{2} = {(a + b)}^{2} - 4 a b$
其中，图形的面积关系能正确解释相应的代数恒等式的有（       ）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，两个正方形的边长分别为a和b，如果a﹣b＝2，ab＝26，那么阴影部分的面积是（）

A、30 B、34 C、40 D、44

查看试题解析
6. 已知 $a$ 和 $b$ 互为倒数， $a + b = 4$ ，求 $(a - b)^{2} =$ ．

查看试题解析
7. $(a - 2 b + 3 c) (a + 2 b - 3 c) =$ ．

查看试题解析
8. 已知 ${(a + b)}^{2} = 36$ ， ${(a - b)}^{2} = 4$ ，则 $a^{2} + b^{2} =$ .

查看试题解析
9. 已知a+ $\frac{1}{a}$ ＝3，
求：

(1)、a²+ $\frac{1}{a^{2}}$ ；

(2)、a- $\frac{1}{a}$ ．

查看试题解析
10. 当我们利用两种不同的方法计算同一图形的面积时，可以得到一个等式．例如，由图①，可得等式： $(a + 2 b) (a + b) = a^{2} + 3 a b + 2 b^{2}$ ．

(1)、由图②，可得等式：；

(2)、利用（1）中所得到的结论，解决下面的问题：
已知 $a + b + c = 11$ ， $a b + b c + a c = 38$ ，求 $a^{2} + b^{2} + c^{2}$ 的值．

查看试题解析
11. 现有长为a ，宽为b的长方形卡片（如图①）若干张，某同学用4张卡片拼出了一个大正方形（不重叠、无缝隙，如图②）．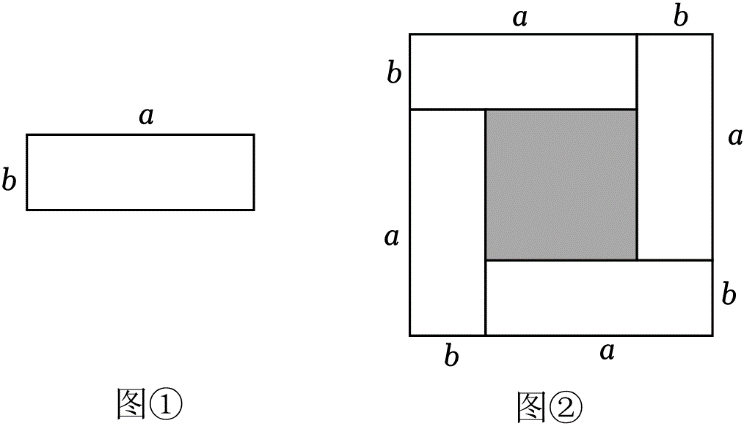

(1)、图②中，大正方形的边长是，阴影部分正方形的边长是．（用含a ， b的式子表示）

(2)、用两种方法表示图②中阴影部分正方形的面积（不化简），并用一个等式表示（a+b）² ，（a﹣b）² ， ab三者之间的数量关系．

(3)、已知a+b＝8，ab＝7，求图②中阴影部分正方形的边长．

查看试题解析

二、能力提升

12. 已知 ${(x - 2023)}^{2} + {(x - 2025)}^{2} = 4050$ ，则 ${(x - 2024)}^{2}$ 的值是（）

A、 $1$ B、 $2025$ C、 $2024$ D、 $2023$

查看试题解析
13. 若k为任意整数，则（2k+3）²-4k²的值总能（）

A、被2整除． B、被3整除． C、被5整除． D、被7整除．

查看试题解析
14. 已知多项式 $A = x^{2} + 4 x + n^{2}$ ，多项式 $B = 2 x^{2} + 6 x + 3 n^{2} + 3$ ．
①若多项式 $x^{2} + 4 x + n^{2}$ 是完全平方式，则 $n = 2$ 或 $- 2$ ；
② $B - A \geq 2$ ；
③若 $A + B = 2 \sqrt{10}$ ， $A \cdot B = - 6$ ，则 $A - B = \pm 8$ ；
④代数式 $5 A^{2} + 9 B^{2} - 12 A \cdot B - 6 A + 2031$ 的最小值为2022．以上结论正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
15. 阅读理解：如果 $a - \frac{1}{a} = 1$ ，我们可以先将等式两边同时平方得到 ${(a - \frac{1}{a})}^{2} = 1$ ，再根据完全平方公式计算得： $a^{2} - 2 a \cdot \frac{1}{a} + \frac{1}{a^{2}} = 1$ ，即 $a^{2} - 2 + \frac{1}{a^{2}} = 1$ ，所以 $a^{2} + \frac{1}{a^{2}} = 3$ ．请运用上面的方法解决下面问题：如果 $x^{2} - 2 x - 1 = 0$ ，则 $x^{2} + \frac{1}{x^{2}}$ 的值为（）

A、8 B、6 C、4 D、2

查看试题解析
16. 计算： ${(- 0.125)}^{99} \times 8^{100} =$ ； $\frac{202 3^{2}}{202 2^{2} + 202 4^{2} - 2} =$ ．

查看试题解析
17. 若 $a = 2005$ ， $b = 2006$ ， $c = 2007$ ，求 $a^{2} + b^{2} + c^{2} - a b - b c - a c =$ .

查看试题解析
18.

(1)、若关于 $a$ ， $b$ 的多项式 $2 (a^{2} - 2 a b + b^{2}) - (3 a^{2} + m a b + 2 b^{2})$ 中不含有 $a b$ 项，则 $m$ 的值为．

(2)、完全平方公式经过适当的变形，可以解决很多数学问题．
例如：若 $a + b = 3$ ， $a b = 1$ ，求 $a^{2} + b^{2}$ 的值．
解： $∵ a + b = 3$ ， $a b = 1$ ， $∴ (a + b)^{2} = 9$ ， $2 a b = 2$ ．
$∴ a^{2} + b^{2} + 2 a b = 9 . ∴ a^{2} + b^{2} = 7$ ．
①如图，点 $C$ 是线段 $A B$ 上的一点，分别以 $A C$ ， $B C$ 为边向直线 $A B$ 两侧作正方形 $B C F G$ ，正方形 $A E D C .$ 设 $A B = 8$ ，两正方形的面积和为 $34$ ，则 $△ A F C$ 的面积为 ▲ ；
②若 $(8 - x) (x - 3) = 7$ ，求 $(8 - x)^{2} + (x - 3)^{2}$ 的值．

查看试题解析

三、拓展创新

19. 若一个整数能表示成 $a^{2} + b^{2} （ a ， b$ 为整数 $）$ 的形式，则称这个数是 “完美数”．例如：因为 $5 = 2^{2} + 1^{2}$ ，所以 5 是一个完美数．已知 $M = x^{2} + 4 y^{2} + 4 x - 12 y + k （ x ， y$ 是整数， $k$ 是常数），要使 $M$ 为“完美数”，则 $k$ 的值是（）

A、13
B、14
C、15
D、16

查看试题解析
20. 如图1是边长分别为m ， n、p的A、B、C三种正方形．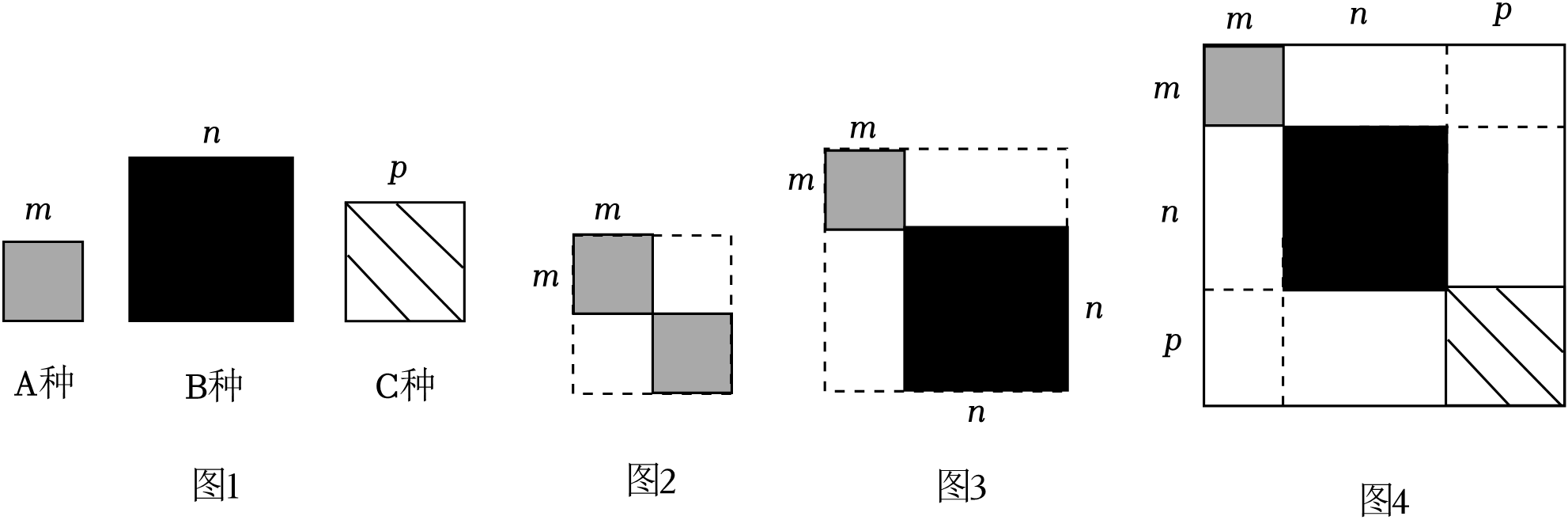

(1)、用两个A种正方形组合成图2的图形，外边框可以围成一个大正方形，则这个大正方形的面积＝（用含m的代数式表示）；

(2)、将一个A种和一个B种正方形组合成图3的图形，外边框可以围成一个大正方形，用两种不同的方法表示这个大正方形的面积：或；则根据这个大正方形面积的不同表示方法，可以得到的乘法公式为；

(3)、将A种、B种和C种正方形组合形成图4的图形，此时的外边框可以围成一个大的正方形，根据（2）中乘法公式的生成过程，直接写出所得到的等式，并令m＝1，n＝3，p＝2，通过计算验证该等式．

查看试题解析