整式的乘法—人教版数学八（上）知识点训练

试卷更新日期：2024-11-24 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 计算（2x+1）（x﹣5）的结果是（　　）

A、2x²﹣9x﹣5 B、2x²﹣9x+5 C、2x²﹣11x﹣5 D、2x²﹣11x+5

查看试题解析
2. 计算（　　） $\div \frac{1}{2} a b^{2} = 8 a$ ，正确的结果是（　　）

A、16 $a^{2} b^{2}$ B、4 $a b$ ² C、 $(4 a b)^{2}$ D、 $(2 a b)^{2}$

查看试题解析
3. 已知 $(x - 2) (x^{2} + m x + n)$ 的乘积项中不含 $x^{2}$ 项，则m的值为（）

A、 $m = 2$ B、 $m = 3$ C、 $m = - 2$ D、 $m = - 3$

查看试题解析
4. 如果（x+a）（x+b）的积中不含x的一次项，那么a，b一定（）

A、互为倒数 B、互为相反数 C、a=b且b=0 D、ab=0

查看试题解析
5. 在一次数学课上，学习了单项式乘多项式，小明回家后，拿出课堂笔记本复习，发现这样一道题：﹣3x（﹣2x²+3x﹣1）＝6x³﹣9x²+□，“□”的地方被墨水弄污了，你认为“□”内应填写（）

A、1 B、﹣1 C、3x D、﹣3x

查看试题解析
6. 今年国庆节长假期间，山西暴雨成灾，临汾某地一个长方形的玉米种植基地被淹，颗粒无收，已知这个基地的长为 $(2 x + 1)$ 米，宽为 $(x - 3)$ 米，则它的面积为（）平方米

A、 $2 x^{2} + x + 3$ B、 $2 x^{2} - 5 x - 3$ C、 $2 x^{2} + x - 3$ D、 $2 x^{2} - 5 x + 3$

查看试题解析
7. 一个长方体的长、宽、高分别为3a－4，2a，a，它的体积等于（）

A、3a³－4a² B、a² C、6a³－8a² D、6a³－8a

查看试题解析
8. 若关于 $x$ 的多项式 $(x^{2} + 2 x + 4) (x + k)$ 展开后不含有一次项，则实数 $k$ 的值为．

查看试题解析
9. 已知 $x + y = 4$ ， $x y = 2$ ，则 $(x - 1) (y - 1) =$ ．

查看试题解析
10. 计算：

(1)、 $4 x^{2} y \cdot （ - x y^{3} ）^{2}$ ；

(2)、 $（ x + y - 3 ）（ x + y + 3 ）$ ．

查看试题解析
11. 如图，某小区有一块长为（2a+3b）米，宽为（3a+2b）米的长方形地块，物业公司计划在小区内修一条平行四边形小路，小路的底边宽为a米，将阴影部分进行绿化．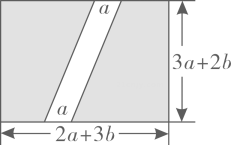

(1)、用含有a、b的式子表示绿化的总面积S；

(2)、若a＝2，b＝4，求出此时绿化的总面积S．

查看试题解析
12. 回答下列问题：

(1)、计算：① $(x + 2) (x + 3) =$ ；② $(x + 2) (x - 3) =$ ．
③ $(x - 2) (x + 3) =$ ；④ $(x - 2) (x - 3) =$ ．

(2)、总结公式 $(x + a) (x + b) = x^{2} +$ $x + a b$

(3)、已知a，b，m均为整数，且 $(x + a) (x + b) = x^{2} + m x + 5$ ．求m的所有可能值．

查看试题解析
13.

(1)、数学课堂上老师留了一道数学题，如图 $①$ ，用式子表示空白部分的面积 $.$ 甲，乙两名同学表示的式子是：甲： $10 \times 6 - 10 x - 6 x$ ；乙： $(10 - x) (6 - x) .$ 正确的学生是．

(2)、如图 $②$ ，有一块长为 $(8 a + 3 b)$ 米，宽为 $(7 a - 3 b)$ 米的长方形空地，计划修筑东西、南北走向的两条道路 $.$ 其余进行绿化，已知两条道路的宽分别为 $2 a$ 米和 $3 a$ 米，求绿化的面积 $. ($ 用含 $a$ ， $b$ 的式子来表示 $)$

查看试题解析

二、能力提升

14. 若 $（ x^{2} + m ） (x^{2} - n x + 4)$ 的乘积中不含 $x^{2}$ 和 $x^{3}$ 项，则 $m + n$ 的值是（）

A、-4 B、-8 C、-2 D、8

查看试题解析
15. 若 $(x^{2} - p x + q) (x - 3)$ 展开后不含 $x$ 的一次项，则 $p$ 与 $q$ 的关系是（）

A、 $p = 3 q$ B、 $p + 3 q = 0$ C、 $q + 3 p = 0$ D、 $q = 3 p$

查看试题解析
16. 如图，甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式，你认为其中正确的有（　　）
①（2a+b）（m+n）；②2a（m+n）+b（m+n）；③m（2a+b）+n（2a+b）；④2am+2an+bm+bn．

A、①② B、③④ C、①②③ D、①②③④

查看试题解析
17. 现有A、B、C三种型号的地板砖，其规格如图所示，若用这三种地板砖铺设一个长为 $3 a + 2 b$ ，宽为 $a + b$ 的长方形地面，则需要B种地砖块．

查看试题解析
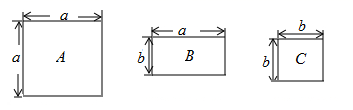18. 小马和小虎两人共同计算一道整式乘法题： $(3 x + a) (2 x + b)$ ，由于小马抄错了 $b$ 的符号，得到的结果为 $6 x^{2} - 17 x + 12$ ；由于小虎漏抄了第一个多项式中 $x$ 的系数，得到的结果为 $2 x^{2} - 5 x - 12$ ．

(1)、求出 $a$ ， $b$ 的值；

(2)、请你计算出这道整式乘法题的正确结果．

查看试题解析
19. 观察下列算式特征，并完成相应任务．
      $(x + 4) (x + 3) = x^{2} + 7 x + 12$ ；

      $(x + 2) (x - 3) = x^{2} - x - 6$ ；

      $(x + 5) (x - 2) = x^{2} + 3 x - 10$ ；

      $(x - 2) (x - 1) = x^{2} - 3 x + 2$ ．

(1)、任务一：发现与表达
请用含字母的算式表示以上算式的一般特征：．

(2)、任务二：问题与解决
如果 $x^{2} + m x + 8 = (x + a) (x + b)$ ，其中 $m ， a ， b$ 均为整数，则 $m$ 的取值有（    ）
$A$ .1个 $B$ .2个 $C$ .3个 $D$ .4个

(3)、任务三：拓展与猜想
若 $(a x + m) (b x + n) = a b x^{2} + p x + q$ ，则 $p =$      ▲     ， $q =$      ▲  ．

查看试题解析

三、拓展创新

20. 阅读材料
小明遇到这样一个问题：求计算 $（ x + 2 ）（ 2 x + 3 ）（ 3 x + 4 ）$ 所得多项式的一次项系数．
小明想通过计算 $（ x + 2 ）（ 2 x + 3 ）（ 3 x + 4 ）$ 所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法．
他决定从简单情况开始，先找 $（ x + 2 ）（ 2 x + 3 ）$ 所得多项式中的一次项系数．通过观察发现：
也就是说，只需用x+2中的一次项系数1乘以2x+3中的常数项3，再用x+2中的常数项2乘以2x+3中的一次项系数2，两个积相加1×3+2×2=7，即可得到一次项系数．
延续上面的方法，求计算 $（ x + 2 ）（ 2 x + 3 ）（ 3 x + 4 ）$ 所得多项式的一次项系数．可以先用x+2的一次项系数1，2x+3的常数项3，3x+4的常数项4，相乘得到12；再用2x+3的一次项系数2，x+2的常数项2，3x+4的常数项4，相乘得到16；然后用3x+4的一次项系数3，x+2的常数项2，2x+3的常数项3，相乘得到18．最后将12，16，18相加，得到的一次项系数为46．
参考小明思考问题的方法，解决下列问题：
（1）计算（2x+1）（3x+2）所得多项式的一次项系数为      ．
（2）计算（x+1）（3x+2）（4x﹣3）所得多项式的一次项系数为      ．
（3）若计算（x²+x+1）（x²﹣3x+a）（2x﹣1）所得多项式的一次项系数为0，则a=      ．
（4）若x²﹣3x+1是x⁴+ax²+bx+2的一个因式，则2a+b的值为      ．

查看试题解析