广东省深圳市坪山区中山中学2022-2023学年七年级下册数学3月月考试卷
试卷更新日期：2023-09-26 类型：月考试卷
一、选择题（每题3分，共30分）
-
1. 计算a2•a5的结果是（ ）A、a10 B、a7 C、a3 D、a82. 某种禽流感病毒变异后的直径为0.00000018米，0.00000018米用科学记数法表示为（ ）A、1.8×10-5米 B、0.18×10-6米 C、1.8×10-7米 D、18×10-8米3. 下列各式中，计算正确的是（ ）A、（x+1）（x-4）＝x2-4 B、（2m+3）2＝2m2+12m+9 C、（y+2）（y-3）＝y2-y-6 D、（5-2y）2＝25-4y24. 下面的四个图形中，∠1与∠2是对顶角的是（ ）A、
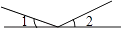B、
C、
D、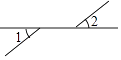
5. 计算（-3）100×的结果是（ ）A、-3 B、3 C、 D、-6. 下列四个命题中，正确的是（ ）A、经过直线外一点，有且只有一条直线与这条直线平行 B、同旁内角相等，两直线平行 C、相等的角是对顶角 D、若∠1+∠2+∠3＝180°，则∠1、∠2、∠3互补7. 若一个角的补角是这个角余角的4倍，则这个角是（ ）A、30° B、45° C、60° D、90°8. 已知a＝255 ， b＝344 ， c＝433 ， 则a、b、c的大小关系为（ ）A、a＞b＞c B、a＞c＞b C、b＞c＞a D、b＞a＞c9. 有下列四种说法：①锐角的补角一定是钝角；②一个角的补角一定大于这个角；③如果两个角是同一个角的补角，那么它们相等；④锐角和钝角互补．其中正确的是（ ）A、①② B、①③ C、①②③ D、①②③④10. 如图，已知点C是线段AB上的一动点，分别以AC ， BC为边向两边作正方形ACDE与正方形CFGB ， 若AB＝8，且两正方形的面积和为S1+S2＝36．则图中阴影部分的面积为（ ）
A、7 B、7.5 C、14 D、15二、填空题（每题3分，共15分）
-
11. 计算2a2b÷（-4ab）的结果是 ．12. 若 ，则n的值为 ．13. 如图，直线a∥b ， 直线c与直线a ， b分别交于点A ， B ． 若∠1＝45°，则∠2＝ ．
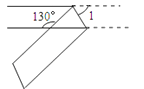
14. 若多项式 是完全平方式，则 的值是 ．15.如图，一个宽度相等的纸条按如图所示方法折叠一下，则∠1= 度．
三、解答题（共55分）
-
16. 计算：(1)、（-1）2020+（-）-2-20210；(2)、x3•x5-（2x4）2+x10÷x2；(3)、[（-xy2z）2-4x3y2z]÷x2y2；(4)、（x+2y）（x-2y）-（x-y）2 ．17. 已知：如图∠AED＝∠C ， ∠DEF＝∠B ， 请你说明∠1与∠2相等吗？为什么？
解：因为∠AED＝∠C（已知）
所以 ▲ ∥ ▲ （ ）
所以∠B+∠BDE＝180°（ ）
因为∠DEF＝∠B（已知）
所以∠DEF+∠BDE＝180°（ ）
所以 ▲ ∥ ▲ （ ）
所以∠1＝∠2（ ）．
18. 已知（am）n＝a6 ， （am）2÷an＝a3(1)、求mn和2m-n的值；(2)、求4m2+n2的值．19. 先化简后计算：（2x+1）（x-2）-（-3x+1）（-3x-1），其中x＝-2．20. 如图，直线a ， b ， a∥b ， 点C在直线b上，∠DCB＝90°，若∠1＝70°，则∠2的度数为多少？
21. 如图所示，已知∠1+∠2＝180°，∠B＝∠3，求证：∠ACB＝∠AED.
22. [知识生成]通常，用两种不同的方法计算同一个图形的面积，可以得到一个恒等式．
例如：如图①是一个长为2a ， 宽为2b的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的形状拼成一个正方形．请解答下列问题：
(1)、请用两种不同的方法求图②中阴影部分的面积：方法1：；方法2：；
(2)、观察图②，请你写出（a+b）2、（a-b）2、ab之间的等量关系是；(3)、根据（2）中的等量关系解决如下问题：若x+y＝6， ， 则（x-y）2＝；(4)、[知识迁移]类似地，用两种不同的方法计算同一几何体的体积，也可以得到一个恒等式．
根据图③，写出一个代数恒等式：；
(5)、已知a+b＝3，ab＝1，利用上面的规律求的值．