吉林省长春市力旺实验中学2023-2024学年八年级上学期开学考试数学试卷
试卷更新日期:2023-09-22 类型:开学考试
一、选择题(本大题共8小题,共24分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 , 下列不等式不一定成立的是( )A、 B、 C、 D、3. 不等式组的解集在数轴上表示正确的是( )A、
2. 若 , 下列不等式不一定成立的是( )A、 B、 C、 D、3. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 如果一个三角形的两边长分别为2和5,则第三边长可能是( )A、2 B、3 C、5 D、85. 下列几种形状的瓷砖中,只用一种不能够铺满地面的是( )A、正六边形 B、正五边形 C、正方形 D、正三角形6. 如图,在和中,点、、、在同一条直线上, , , 只添加一个条件,不能判断≌的是( )
4. 如果一个三角形的两边长分别为2和5,则第三边长可能是( )A、2 B、3 C、5 D、85. 下列几种形状的瓷砖中,只用一种不能够铺满地面的是( )A、正六边形 B、正五边形 C、正方形 D、正三角形6. 如图,在和中,点、、、在同一条直线上, , , 只添加一个条件,不能判断≌的是( ) A、 B、 C、 D、7. 如图,将绕点逆时针旋转后得到 , 若 , 则的度数是( )
A、 B、 C、 D、7. 如图,将绕点逆时针旋转后得到 , 若 , 则的度数是( )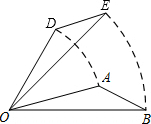 A、 B、 C、 D、8. 若关于的方程的解是非负数,则的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、8. 若关于的方程的解是非负数,则的取值范围是( )A、 B、 C、 D、二、填空题(本大题共6小题,共18分)
-
9. 当时,代数式与的值互为相反数.10. 命题“若 , 则”是命题.(填“真”或“假”)11. 如图, , , 则的度数为 .
 12. 如图,、、在同一直线上,≌ , , 那么度.
12. 如图,、、在同一直线上,≌ , , 那么度. 13. 如图,小陈从点出发,前进米后向右转 , 再前进米后又向右转 , , 这样一直走下去,他第一次回到出发点时一共走了米.
13. 如图,小陈从点出发,前进米后向右转 , 再前进米后又向右转 , , 这样一直走下去,他第一次回到出发点时一共走了米. 14. 如图,中, , 边上有一点 , 使得 , 将沿翻折得 , 此时 , 则度.
14. 如图,中, , 边上有一点 , 使得 , 将沿翻折得 , 此时 , 则度.
三、解答题(本大题共10小题,共78分。解答应写出文字说明,证明过程或演算步骤)
-
15. 解下列方程、不等式.(1)、;(2)、 .16. 解下列方程组、不等式组.(1)、;(2)、 .17. 我国古代数学名著九章算术中有一道阐述“盈不足术”的问题,原文如下:今有共买物,人出八,盈三;人出七,不足四问人数、物价各几何?意思是:几个人一起去购买某物品,如果每人出钱,则多了钱;如果每人出钱,则少了钱问有多少人,物品的价值是多少?请你解决此问题.
 18. 已知关于 , 的二元一次方程组的解满足 , 求的值.19. 如图,方格纸中的每个小方格都是边长为个单位长度的正方形,每个小正方形的顶点叫格点,的顶点均在格点上, , 也在格点上.
18. 已知关于 , 的二元一次方程组的解满足 , 求的值.19. 如图,方格纸中的每个小方格都是边长为个单位长度的正方形,每个小正方形的顶点叫格点,的顶点均在格点上, , 也在格点上. (1)、画出先向右平移个单位长度,再向下平移个单位长度得到的;(2)、画出关于直线对称的;(3)、画出绕点按逆时针方向旋转后所得的;(4)、与组成的图形是轴对称图形吗?若是轴对称图形,请画出对称轴.20. 将沿的方向平移得到 .(1)、若 , , 求的度数;(2)、若的周长为 , , , 连结 , 则四边形的周长为 .
(1)、画出先向右平移个单位长度,再向下平移个单位长度得到的;(2)、画出关于直线对称的;(3)、画出绕点按逆时针方向旋转后所得的;(4)、与组成的图形是轴对称图形吗?若是轴对称图形,请画出对称轴.20. 将沿的方向平移得到 .(1)、若 , , 求的度数;(2)、若的周长为 , , , 连结 , 则四边形的周长为 . 21. 如图,在中,是延长线上一点,满足 , 过点作 , 且 , 连接并延长,分别交 , 于点 , .(1)、求证:≌;(2)、若 , , 求的长度.
21. 如图,在中,是延长线上一点,满足 , 过点作 , 且 , 连接并延长,分别交 , 于点 , .(1)、求证:≌;(2)、若 , , 求的长度. 22. 高安腐竹始于唐代,距今已有多年的历史“五一”期间,高安市对、两种品牌的腐竹举行展销活动若购买箱品牌腐竹和箱品牌腐竹共需要元,购买箱品牌腐竹和箱品牌腐竹则需要元.(1)、求、品牌腐竹每箱售价各为多少元?(2)、小王计划购买、两种品牌腐竹共箱,预算总费用不超过元,则品牌腐竹最多能购买多少箱?23. 综合与实践
22. 高安腐竹始于唐代,距今已有多年的历史“五一”期间,高安市对、两种品牌的腐竹举行展销活动若购买箱品牌腐竹和箱品牌腐竹共需要元,购买箱品牌腐竹和箱品牌腐竹则需要元.(1)、求、品牌腐竹每箱售价各为多少元?(2)、小王计划购买、两种品牌腐竹共箱,预算总费用不超过元,则品牌腐竹最多能购买多少箱?23. 综合与实践小明遇到这样一个问题,如图 , 中, , , 点为的中点,求的取值范围小明的做法是:如图 , 延长到 , 使 , 连接 , 构造≌ , 经过推理和计算使问题得到解决.

请回答:
(1)、小明证明≌用到的判定定理是:____A、 B、 C、 D、(2)、的取值范围是 .(3)、小明总结:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.参考小明思考问题的方法,解决问题:
如图3,在正方形各角都为直角中,为边的中点,、分别为边上的点,若 , , , 求的长.
24. 如图,在中, , , , , 动点从点出发以每秒个单位长度的速度沿运动到点停止,同时点从点出发,以每秒个单位长度的速度沿运动,到点停止,若设点运动的时间是秒 .(1)、点到达点时,;到时,秒;(2)、当时,求的值;(3)、当点在边上时;①当的面积等于时,直接写出的值.
②当点或点到边和边的距离相等时,直接写出的值.
