湖南省长沙市梅溪湖中学2023-2024学年九年级上学期数学入学考试试卷

试卷更新日期：2023-09-22 类型：开学考试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1. 下列方程中，属于一元二次方程的是（）

A、 $x^{2} + \frac{1}{x} = 2$ B、 $x^{2} - x y = 2$ C、 $x^{2} - 2 x - 3 = 0$ D、 $2 (x - 1) = x$

查看试题解析
2. 点 $P (1 ， 3)$ 在正比例函数 $y = k x (k \neq 0)$ 的图象上，则 $k$ 的值为（）

A、 $\frac{1}{3}$ B、2 C、3 D、4

查看试题解析
3. 在 $▱ A B C D$ 中，若 $∠ A + ∠ C = 140 °$ ，则 $∠ B$ 的度数是（）

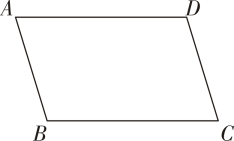A、70° B、110° C、120° D、140°

查看试题解析
4. 将直线 $y = 2 x$ 向下平移1个单位得到的直线是（）

A、 $y = - 2 x + 1$ B、 $y = - 2 x - 1$ C、 $y = 2 x + 1$ D、 $y = 2 x - 1$

查看试题解析
5. 某企业参加“科技创新企业百强”评选，创新能力、创新价值、创新影响三项得分分别为8分，9分，7分，若将三项得分依次按5：3：2的比例计算总成绩，则该企业的总成绩为（）

A、8分 B、8.1分 C、8.2分 D、8.3分

查看试题解析
6. 已知关于 $x$ 的方程 $x^{2} - 2 x + m = 0$ 有两个相等实数根，则 $m$ 的值为（）

A、3 B、2 C、1 D、0

查看试题解析
7. 在平面直角坐标系 $x O y$ 中，点 $A (2 ， y_{1})$ ， $B (3 ， y_{2})$ 在函数 $y = - 3 x + b$ 的图象上，则（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、以上都有可能

查看试题解析
8. 如图，在平面直角坐标系 $x O y$ 中，四边形 $A B C D$ 是菱形， $∠ A B C = 120 °$ ，点 $B$ 的坐标为 $(0 ， - 3)$ ，则点 $A$ 的坐标为（）

A、 $(- 3 \sqrt{3} ， 0)$ B、 $(3 \sqrt{3} ， 0)$ C、 $(- 6 ， 0)$ D、 $(6 ， 0)$

查看试题解析
9. 某商店购进一种商品，单价为 $30$ 元．试销中发现这种商品每天的销售量 $P$ （件）与每件的销售价 $x$ （元）满足关系： $P = 100 - 2 x$ ．若商店在试销期间每天销售这种商品获得 $200$ 元的利润，根据题意，下面所列方程正确的是（）

A、 $(x - 30) (100 - 2 x) = 200$ B、 $x (100 - 2 x) = 200$ C、 $(30 - x) (100 - 2 x) = 200$ D、 $(x - 30) (2 x - 100) = 200$

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $∠ C = 67.5 °$ ，点 $D$ 为 $A B$ 上一点，点 $E$ 为 $A C$ 的中点，连接 $D E$ .若 $∠ A E D = ∠ A$ ，则 $\frac{D E}{B C}$ 的值为（）

A、 $\frac{\sqrt{3}}{2}$ B、1 C、 $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析

二、填空题（共6小题，每小题3分，共18分）

11. 函数 $y = \frac{6}{x - 2}$ 中，自变量 $x$ 的取值范围是.

查看试题解析
12. 已知 $m$ 是方程 $x^{2} - 4 x - 3 = 0$ 的一个实数根，则 $m^{2} - 4 m + 2023$ 的值是．

查看试题解析
13. 如图，矩形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ，再添加一个条件，使得四边形 $A B C D$ 是正方形，这个条件可以是（写出一个条件即可）.

查看试题解析
14. 如图，大正方形是由四个全等的直角三角形和面积分别为 $S_{1}$ ， $S_{2}$ 的两个正方形所拼成的.若直角三角形的斜边长为2，则 $S_{1} + S_{2}$ 的值为.

查看试题解析
15. 如图， $△ A B C$ 中， $A C = 4$ ， $B C = 3$ ， $A B = 5$ ， $A D$ 为 $△ A B C$ 的角平分线，则 $C D$ 的长度为.

查看试题解析
16. 如图， $A B = 12$ ， $∠ A = 45 °$ ，点 $D$ 是射线 $A F$ 上的一个动点， $D C ⊥ A B$ ，垂足为点 $C$ ，点 $E$ 为 $D B$ 的中点，则线段 $C E$ 的长的最小值为.

查看试题解析

三、解答题（共9小题，其中17、18、19每小题6分，20、21每小题8分，22、23每小题9分，24、25每小题10分，共72分）

17. 解方程： $2 x^{2} - 3 x + 1 = 0$

查看试题解析
18. 如图，在 $▱ A B C D$ 中， $∠ B A D$ ， $∠ A D C$ 的平分线 $A F$ ， $D E$ 分别与线段 $B C$ 交于点 $F$ ， $E$ ， $A F$ 与 $D E$ 交于点 $G$ .

(1)、求证： $A F ⊥ D E$ ；

(2)、求证： $B F = C E$ .

查看试题解析
19. 如图，一次函数 $y = - \frac{4}{3} x + 4$ 的图象与 $x$ 轴和 $y$ 轴分别交于点 $A$ 和点 $B$ .

(1)、求点 $A$ 和点 $B$ 的坐标；

(2)、求 $O$ 点到直线 $A B$ 的距离.

查看试题解析

20. 某校为了解全校1500名学生的视力情况，随机抽取了

m

名学生调查，将抽取的学生视力情况绘制成不完整的频数分布表和扇形统计图.

组别	视力	人数
$A$	$4.0 \leq x < 4.3$	$n$
$B$	$4.3 \leq x < 4.6$	12
$C$	$4.6 \leq x < 4.9$	18
$D$	$4.9 \leq x < 5.2$	21
$E$	$5.2 \leq x < 5.5$	6

请你根据图表提供的信息，回答下列问题：

(1)、填空，

m =

，

n =

，

C

组所在扇形的圆心角等于°；

(2)、此次抽样调查中，视力的中位数在组别，众数在组别；

(3)、如果视力在第

D

，

E

两组范围内（4.9及以上）均属视力良好.请估计该校视力良好的学生有多少名？

查看试题解析

21. 关于 $x$ 的一元二次方程 $x^{2} - (2 k - 1) x + k^{2} + 1 = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ .

(1)、求实数 $k$ 的取值范围；

(2)、若方程的两实数根 $x_{1}$ ， $x_{2}$ 满足 $x_{1} + x_{2} = - x_{1} \cdot x_{2}$ ，求 $k$ 的值.

查看试题解析
22. 受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素，我市某汽车零部件生产企业的利润逐年提高，据统计，2016年利润为2亿元，2018年利润为2.88亿元.

(1)、求该企业从2016年到2018年利润的年平均增长率；

(2)、若2019年保持前两年利润的年平均增长率不变，该企业2019年的利润能否超过3.4亿元？

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ ， $E$ ， $F$ 分别为 $B C$ ， $A B$ ， $A C$ 的中点.

(1)、求证：四边形 $A E D F$ 是菱形；

(2)、若 $A B = 6$ ， $B C = 10$ ，求四边形 $A E D F$ 的面积.

查看试题解析
24. 著名数学家高斯曾说过：“如果别人思考数学的真理像我一样深入持久，他也会找到我的发现”，我们向伟人看齐，将这种勤思善学、砺能笃行的精神运用于日常的数学学习中来，尝试发现新的惊喜.
【提出问题】

我们曾探究过一元二次方程根与系数的关系，如果一元二次方程的系数按照某种规律发生变化，原方程的根与新方程的根是否也会产生某种联系？

【构造关系】

将一元二次方程的二次项系数、一次项系数和常数项按照 $n ： 1 ： \frac{1}{n}$ 的比例放大或缩小，其中 $n \neq 0$ ，我们称新方程为原方程的“系变方程”，系变倍数为 $n$ .

(1)、当系变倍数为3时，求解一元二次方程 $x^{2} + 2 x - 3 = 0$ 的“系变方程”.

(2)、【自能探究】已知某一元二次方程有两个实数根 $x_{1}$ ， $x_{2}$ ，当 $n = 2$ 时，其“系变方程”也有两个实数根 $p$ 、 $q$ ，且 $x_{1} x_{2} = 1$ ，求 $\frac{q}{p} + \frac{p}{q} - (\frac{4}{p} + \frac{1}{4 q}) + 17$ 的最小值.

(3)、已知关于 $x$ 的方程 ${(3 x^{2} + t x - 2)}^{2} + {(- 2 x^{2} - t x + 3)}^{2} = {(x^{2} + 1)}^{2}$ 有四个实数根 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 、 $x_{4}$ ，问是否存在定值 $k$ ，对于任意实数 $t$ ，都满足 $\frac{x_{1}}{x_{2}} = \frac{x_{3}}{x_{4}} = k$ ，若存在，请求出 $k$ 的值.若不存在，请说明理由.

查看试题解析
25. 如图，在平面直角坐标系中，平行四边形 $O A B C$ 中点 $A$ 的坐标为 $(- 3 ， - 4)$ ，点 $B$ 坐标为 $(6 ， - 4)$ ， $A B$ 与 $y$ 轴交于点 $M$ ，点 $D$ 是射线 $O C$ 上一动点，点 $E$ 是 $O D$ 的中点，连接 $A E$ 交 $y$ 轴于点 $F$ ，过点 $D$ 作 $D G ⊥ O C$ 交 $A E$ 延长线于点 $G$ ，交 $A B$ 于点 $H$ ，连接 $O G$ .

(1)、若 $O D = 4$ ，求 $O G$ 的长.

(2)、若 $∠ O A E = 2 ∠ G O E - ∠ G E D$ ，求 $O D$ 的长.

(3)、①连接 $D F$ ，问直线 $D F$ 是否经过一定点，若经过，请求出该定点；若不经过，请说明理由；
②连接 $F B$ ， $B D$ ，若 $∠ D F B = 30 °$ ，求 $O D$ 的长.

查看试题解析