江苏省无锡市积余教育集团2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 我国新能源汽车产业发展取得了明显成效,逐渐进入市场化驱动阶段.下列新能源汽车图标中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法中正确的是( )A、要反映一个家庭每年用于旅游的费用占总支出的百分比宜采用条形统计图 B、概率很小的事件是不可能事件 C、检查“天舟一号”飞船各零件的安全性,可采用抽样调查的办法 D、射击运动员射击一次,命中靶心是随机事件3. 下列计算正确的是( )A、 B、 C、 D、4. 下列条件中,能使菱形 为正方形的是( )A、 B、 C、 D、 平分5. 下列分式中,与 的值相等的是( )A、 B、 C、 D、6. 下列关于反比例函数的描述,正确的是( )A、它的图象经过点 B、图象的两支分别在第一、三象限 C、当时, D、时,y随x的增大而减小7. 如图,在中, , 以点B为旋转中心把按顺时针方向旋转得到 , 点恰好落在上,连接 , 则度数为( )
2. 下列说法中正确的是( )A、要反映一个家庭每年用于旅游的费用占总支出的百分比宜采用条形统计图 B、概率很小的事件是不可能事件 C、检查“天舟一号”飞船各零件的安全性,可采用抽样调查的办法 D、射击运动员射击一次,命中靶心是随机事件3. 下列计算正确的是( )A、 B、 C、 D、4. 下列条件中,能使菱形 为正方形的是( )A、 B、 C、 D、 平分5. 下列分式中,与 的值相等的是( )A、 B、 C、 D、6. 下列关于反比例函数的描述,正确的是( )A、它的图象经过点 B、图象的两支分别在第一、三象限 C、当时, D、时,y随x的增大而减小7. 如图,在中, , 以点B为旋转中心把按顺时针方向旋转得到 , 点恰好落在上,连接 , 则度数为( )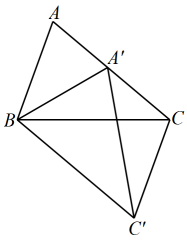 A、 B、 C、 D、8. 关于x的方程的解是负数,则m的取值范围是( )A、 B、且 C、 D、且9. 如图1,点P从菱形的顶点A出发,沿以的速度匀速运动到点B,点P运动时的面积随时间变化的关系如图2,则a的值为( )
A、 B、 C、 D、8. 关于x的方程的解是负数,则m的取值范围是( )A、 B、且 C、 D、且9. 如图1,点P从菱形的顶点A出发,沿以的速度匀速运动到点B,点P运动时的面积随时间变化的关系如图2,则a的值为( )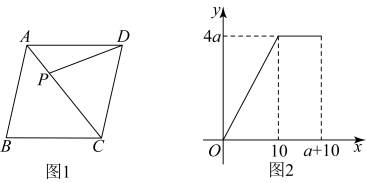 A、8 B、 C、6 D、10. 在正方形中,点E、F在对角线上, , 若点E、F是的三等分点,点P在正方形的边上从点A开始按逆时针方向运动一周,直至返回点A,则此过程中满足为整数的点P个数为( )
A、8 B、 C、6 D、10. 在正方形中,点E、F在对角线上, , 若点E、F是的三等分点,点P在正方形的边上从点A开始按逆时针方向运动一周,直至返回点A,则此过程中满足为整数的点P个数为( )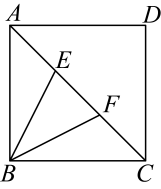 A、38 B、36 C、20 D、22
A、38 B、36 C、20 D、22二、填空题
-
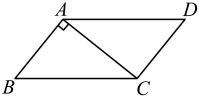
11. 若式子 在实数范围内有意义,则x的取值范围是 .12. 在一个不透明的盒子中装有12个白球和若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率为 ,则黄球有个.13. 当时,分式的值为零.14. 最简二次根式与是同类二次根式,则 .15. 如图,在中, , 若 , 则的度数是.
 16. 某市为治理污水,需要铺设一段全长为的污水排放管道,铺设后,为加快工期,后来每天的工效比原计划增加 , 结果共用30天完成这一任务.如果设原计划每天铺设管道,那么可列方程为 .17. 如图,过y轴正半轴上一点P作x轴的平行线,分别与反比例函数和的图象相交于点A和点B,C是x轴上一点.若的面积为4,则k的值为 .
16. 某市为治理污水,需要铺设一段全长为的污水排放管道,铺设后,为加快工期,后来每天的工效比原计划增加 , 结果共用30天完成这一任务.如果设原计划每天铺设管道,那么可列方程为 .17. 如图,过y轴正半轴上一点P作x轴的平行线,分别与反比例函数和的图象相交于点A和点B,C是x轴上一点.若的面积为4,则k的值为 .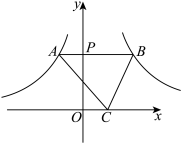 18. 如图,菱形的对角线长度为6,边长 , M为菱形外一个动点,满足 , N为中点,连接 . 则当M运动的过程中,长度的最大值为.
18. 如图,菱形的对角线长度为6,边长 , M为菱形外一个动点,满足 , N为中点,连接 . 则当M运动的过程中,长度的最大值为.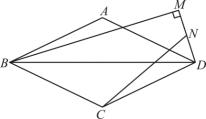
三、解答题
-
19. 计算:(1)、;(2)、20.(1)、化简:;(2)、解方程: .21. 先化简,再求值: ,其中 .22. 请仅用无刻度的直尺按下列要求作图,保留作图痕迹,不写作法:
 (1)、如图1,在四边形中, , , , 作一个菱形(写答句);(2)、如图2,四边形是平行四边形,点在上, , 作的平分线23. 如图,在中,是边上的中线,E是的中点,过点C作的平行线交的延长线于点F,连接 .
(1)、如图1,在四边形中, , , , 作一个菱形(写答句);(2)、如图2,四边形是平行四边形,点在上, , 作的平分线23. 如图,在中,是边上的中线,E是的中点,过点C作的平行线交的延长线于点F,连接 . (1)、求证:四边形为平行四边形;(2)、若 , 试判断四边形的形状,并说明理由.24. 某校学生会倡导的“牵手特殊教育”自愿捐款活动,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知、两组捐款人数的比为 .
(1)、求证:四边形为平行四边形;(2)、若 , 试判断四边形的形状,并说明理由.24. 某校学生会倡导的“牵手特殊教育”自愿捐款活动,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知、两组捐款人数的比为 .组别
捐款额x/元
人数
A
a
B
100
C
D
E

请结合以上信息解答下列问题:(1)、a= , 本次调查样本的容量是;(2)、求C组的人数;(3)、扇形统计图中B类部分所对应扇形的圆心角的度数为°;(4)、根据统计情况,估计该校参加捐款的4500名学生有多少人的捐款额在C组或D组.25. 如图,一次函数的图象与反比例函数的图象交于点A,与x轴交于点B,与y轴交于点C,轴于点D, , 点C关于直线的对称点为点E.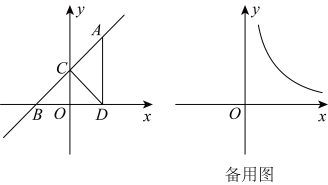 (1)、点E是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.
(1)、点E是否在这个反比例函数的图象上?请说明理由;(2)、连接、 , 若四边形为正方形.①求k、b的值;
②若点P在y轴上,当最大时,求点P的坐标.
26. 将一个矩形纸片放置在平面直角坐标系中,分别在x轴,y轴的正半轴上,点B坐标为 .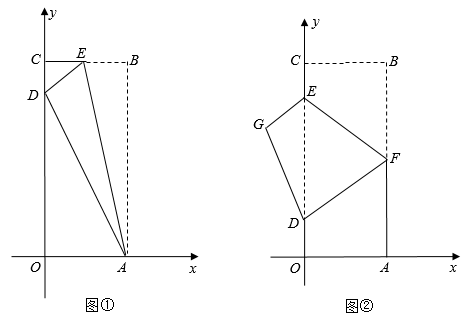
(Ⅰ)如图①,将矩形纸片折叠,使点B落在y轴上的点D处,折痕为线段 , 求点D坐标;
(Ⅱ)如图②,点E,F分别在边上,将矩形纸片沿线段折叠,使得点B与点重合,求点C的对应点G的坐标;
(Ⅲ)在(Ⅱ)的条件下,若点P是坐标系内任意一点,点Q在y轴上,使以点D,F,P,Q为顶点的四边形是菱形,请直接写出满足条件的点P的坐标.