2023年高考数学真题分类汇编7:立体几何
试卷更新日期:2023-07-18 类型:二轮复习
一、填空题
-
1. 在正方体中,E,F分别为CD,的中点,则以EF为直径的球面与正方体每条棱的交点总数为 .
-
2. 已知点均在半径为2的球面上,是边长为3的等边三角形,平面 , 则 .
-
3. 空间内存在三点 , 满足 , 在空间内取不同两点(不计顺序),使得这两点与可以组成正四棱锥,求方案数为 ;
-
4. 底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为2,高为3的正四棱锥,所得棱台的体积为 .
-
5. 在正四棱台 中, , 则该棱台的体积为.
二、选择题
-
6. 在三棱锥中,是边长为2的等边三角形, , 则该棱锥的体积为( )A、1 B、 C、2 D、3
-
7. 在四棱锥中,底面为正方形, , 则的面积为( )A、 B、 C、 D、
-
8. 在三棱锥中,线段上的点满足 , 线段上的点满足 , 则三棱锥和三棱锥的体积之比为( )A、 B、 C、 D、
-
9. 如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则该零件的表面积为( )
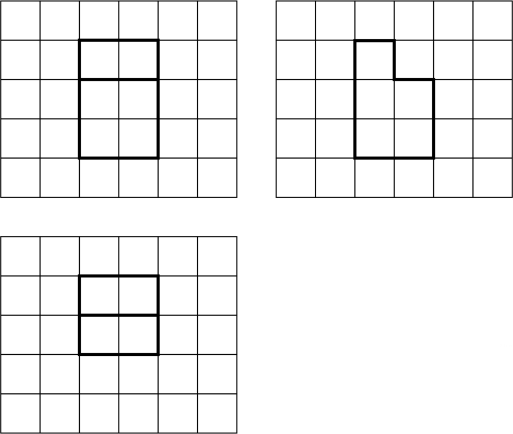 A、24 B、26 C、28 D、30
A、24 B、26 C、28 D、30 -
10. 已知为等腰直角三角形,AB为斜边,为等边三角形,若二面角为 , 则直线CD与平面ABC所成角的正切值为( )A、 B、 C、 D、
-
11. 已知圆锥PO的底面半径为 , O为底面圆心,PA,PB为圆锥的母线, , 若的面积等于 , 则该圆锥的体积为( )A、 B、 C、 D、
-
12. 如图,网格纸上绘制的是个零件的三视图,网格小正方形的边长为1,则该零件的表面积( )
 A、24 B、26 C、28 D、30
A、24 B、26 C、28 D、30 -
13. 已知圆锥的顶点为 , 底面圆心为 , 为底面直径, , , 点在底面圆周上,且二面角为45°,则( )A、该圆锥的体积为 B、该圆锥的侧面积为 C、 D、的面积为
-
14. 下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有( )A、直径为0.99m的球体 B、所有棱长均为1.4m的四面体 C、底面直径为0.01m,高为1.8m的圆柱体 D、底面直径为1.2m,高为0.01m的圆柱体
三、解答题
-
15. 在三棱柱中, , 底面ABC, , 到平面的距离为1.
 (1)、求证:;(2)、若直线与距离为2,求与平面所成角的正弦值.
(1)、求证:;(2)、若直线与距离为2,求与平面所成角的正弦值. -
16. 如图,在三棱柱中,平面 .
 (1)、证明:平面平面;(2)、设 , 求四棱锥的高.
(1)、证明:平面平面;(2)、设 , 求四棱锥的高. -
17. 三棱台中,若面 , 分别是中点.
 (1)、求证://平面;(2)、求平面与平面所成夹角的余弦值;(3)、求点到平面的距离.
(1)、求证://平面;(2)、求平面与平面所成夹角的余弦值;(3)、求点到平面的距离. -
18. 如图,在三棱锥中, , , , , BP,AP,BC的中点分别为D,E,O, , 点F在AC上,.
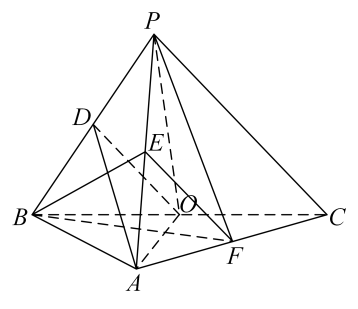 (1)、证明:平面;(2)、证明:平面平面BEF;(3)、求二面角的正弦值.
(1)、证明:平面;(2)、证明:平面平面BEF;(3)、求二面角的正弦值. -
19. 如图,在三棱锥中, , , , , 的中点分别为 , 点在上, .
 (1)、求证://平面;(2)、若 , 求三棱锥的体积。
(1)、求证://平面;(2)、若 , 求三棱锥的体积。 -
20. 已知直四棱柱.
 (1)、求证:面;(2)、若直四棱柱的体积为36,求二面角的大小.
(1)、求证:面;(2)、若直四棱柱的体积为36,求二面角的大小. -
21. 如图,三棱锥中,60°,E为BC中点.
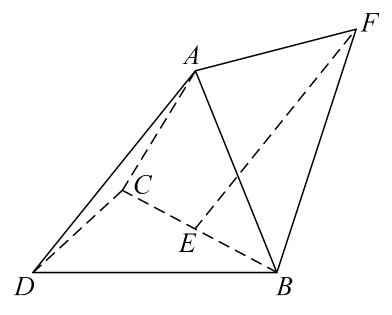 (1)、证明:(2)、点F满足 ,求二面角D-AB-F的正弦值.
(1)、证明:(2)、点F满足 ,求二面角D-AB-F的正弦值. -
22. 如图, 在正四棱柱 中, . 点 分别在棱 上, , .
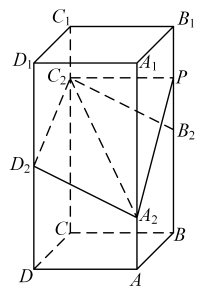 (1)、证明:;(2)、点在棱 上, 当二面角 为时, 求.
(1)、证明:;(2)、点在棱 上, 当二面角 为时, 求.
