辽宁省锦州市2022年九年级下学期质量检测(一)数学试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
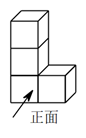
1. 2022的相反数是( )A、﹣2022 B、2022 C、 D、2. 如图所示的几何体的俯视图是( )
 A、
A、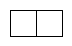 B、
B、 C、
C、 D、
D、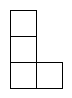 3. 自1983年以来,中央电视台春节联欢晚会成为了全国人民过年的一道“文化大餐”,40年来的不断努力赢得了全国人民的坚持和守望.据初步统计,截至1月31日24时,《2022年春节联欢晚会》电视端直播平均收视率达 .新媒体点播用户触达49.32亿次,相对去年增加明显.数据49.32亿用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 某小组同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,下列说法正确的是( )
3. 自1983年以来,中央电视台春节联欢晚会成为了全国人民过年的一道“文化大餐”,40年来的不断努力赢得了全国人民的坚持和守望.据初步统计,截至1月31日24时,《2022年春节联欢晚会》电视端直播平均收视率达 .新媒体点播用户触达49.32亿次,相对去年增加明显.数据49.32亿用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 某小组同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,下列说法正确的是( )劳动时间(h)
3
3.5
4
4.5
人数
2
4
3
1
A、中位数是3.5,平均数是3.65 B、众数是3.5,平均数是3.7 C、中位数是4,平均数是3.7 D、众数是4,平均数是3.656. 将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )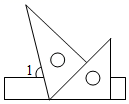 A、45° B、65° C、75° D、85°7. 如图,在 中, , , .①以点A为圆心,以适当长为半径画弧,交 于点G,交 于点H;再分别以点G,H为圆心,以大于 的长为半径画弧,两弧在 的内部相交于点E;作射线 交 边于点D;②分别以点A,D为圆心,以大于 的长为半径画弧,两弧相交于点M,N;作直线 交AD于点F.则 的面积为( )
A、45° B、65° C、75° D、85°7. 如图,在 中, , , .①以点A为圆心,以适当长为半径画弧,交 于点G,交 于点H;再分别以点G,H为圆心,以大于 的长为半径画弧,两弧在 的内部相交于点E;作射线 交 边于点D;②分别以点A,D为圆心,以大于 的长为半径画弧,两弧相交于点M,N;作直线 交AD于点F.则 的面积为( )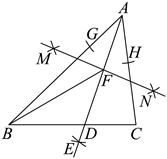 A、1.15 B、1 C、0.8 D、0.758. 如图,在 中, , , , ,点B,C,D,E在同一直线上(点C和点D重合), 从点C出发沿射线 方向以每秒1个单位长度的速度匀速运动,当点E运动到点C处时,停止运动.设运动时间为x秒, 和 重叠部分的面积为y,下列图象能反映y与x之间函数关系的是( )
A、1.15 B、1 C、0.8 D、0.758. 如图,在 中, , , , ,点B,C,D,E在同一直线上(点C和点D重合), 从点C出发沿射线 方向以每秒1个单位长度的速度匀速运动,当点E运动到点C处时,停止运动.设运动时间为x秒, 和 重叠部分的面积为y,下列图象能反映y与x之间函数关系的是( )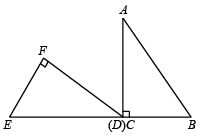 A、
A、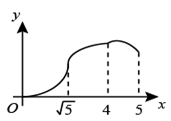 B、
B、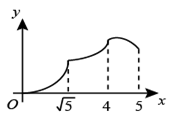 C、
C、 D、
D、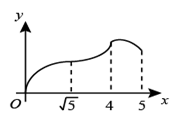
二、填空题
-
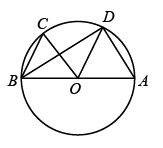
9. 因式分解: .10. 在一个不透明的盒子中,装有若干张完全相同的卡片,从盒子中取出20张卡片并做标记后放回盒中.现将卡片充分摇匀后,随机摸出一张卡片,记下该卡片是否有标记后再放回盒子中.不断重复这一过程,统计发现,摸到有标记卡片的频率稳定在0.02附近,由此估计盒子中卡片的数量为张.11. 某研究员从甲、乙两块试验田中各随机抽取100株杂交水稻苗测试高度,整理数据后得到这两组数据的平均数分别为 , ,方差分别 , ,则杂交水稻长势比较整齐的试验田是(填“甲”或“乙”).12. 若一元二次方程 没有实数根,则常数项c的最小整数值为 .13. 如图, 是 的直径,C,D是 上的两点, ,连接 , ,若 ,则 的大小为 .
 14. 如图,A是反比例函数 图象上一点, 轴于点B,C是x轴正半轴上一点,且满足 , 与y轴交于点D,若 ,则 .
14. 如图,A是反比例函数 图象上一点, 轴于点B,C是x轴正半轴上一点,且满足 , 与y轴交于点D,若 ,则 .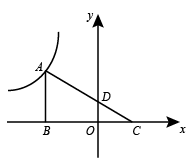 15. 如图,在菱形 中,F为 边上一点,将 沿 折叠,点C恰好落在 延长线上的点E处,连接 交 于点G,若 , ,则 的长为 .
15. 如图,在菱形 中,F为 边上一点,将 沿 折叠,点C恰好落在 延长线上的点E处,连接 交 于点G,若 , ,则 的长为 .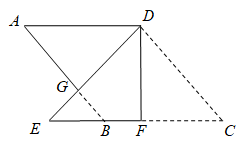 16. 如图,在平面直角坐标系中,直线 : 与直线 : 分别交y轴于点A,B.以 为直角边在其左侧作 ,且另一直角边满足 ,过点C作 分别交直线 与 于点 , ;以 为直角边在其左侧作 ,且另一直角边满足 ,过点 作 分别交直线 与 于点 , ;以 为直角边在其左侧作 ,且另一直角边满足 ……按照此规律进行下去,则 的面积为 .
16. 如图,在平面直角坐标系中,直线 : 与直线 : 分别交y轴于点A,B.以 为直角边在其左侧作 ,且另一直角边满足 ,过点C作 分别交直线 与 于点 , ;以 为直角边在其左侧作 ,且另一直角边满足 ,过点 作 分别交直线 与 于点 , ;以 为直角边在其左侧作 ,且另一直角边满足 ……按照此规律进行下去,则 的面积为 .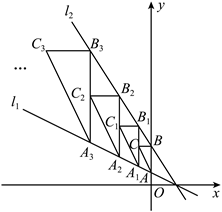
三、解答题
-
17. 先化简,再求值: ,其中 .18. 某校对九年级学生进行“综合素质”评价,评价结果分优秀,良好,合格,不合格四个等级(分别用A,B,C,D表示),现从中随机抽取若干名学生的“综合素质”的等级作为样本进行数据分析,并绘制下列两幅不完整的统计图.请根据统计图提供的信息,解答下列问题.
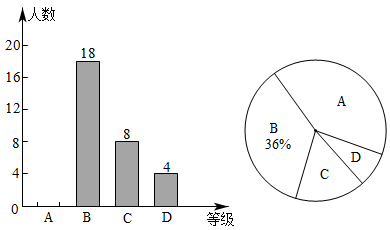 (1)、本次随机抽取的学生有名,等级为优秀(A)的学生人数所占的百分比是;(2)、在扇形统计图中,等级为合格(C)的学生所在扇形的圆心角度数是;(3)、将条形统计图补充完整;(4)、若该校九年级学生共1200名,请根据以上调查结果估算,等级为良好及良好以上的学生共有多少名?19. 北京冬奥会已落下帷幕,它惊艳了全世界,我国取得了9金4银2铜的历史最好成绩.本届奥运会有新星谷爱凌和苏翊鸣(分别用A,B表示)的诞生,也有老将徐梦桃和齐广璞(分别用C,D表示)的圆梦.为了传承并发扬奥运精神,某校开展“讲奥运冠军故事,传承奥运精神”的主题班会.(1)、小明从这四位奥运冠军中随机选取一位是谷爱凌的概率是;(2)、李亮小组从这四位奥运冠军中随机选取两位讲他们的故事,请用列表或面树状图的方法求李亮小组选取苏翊鸣和齐广璞的概率。20. 某社区为了创建干净整洁、和谐文明的社区环境,准备购买A,B两种分类垃圾桶,通过市场调研得知:A种垃圾桶每组的单价是B种垃圾桶每组单价的1.5倍,用7200元购买A种垃圾桶的组数比用6000元购买B种垃圾桶少5组.(1)、求A,B两种垃圾桶每组单价分别是多少元;(2)、该社区计划用不超过12000元的资金购买A,B两种垃圾桶共40组,则最多可以购买A种垃圾桶多少组?21. 某数学兴趣小组测量一栋高层住宅楼 的高度,在住宅楼 对面的多层洋房 的楼底C处,测得住宅楼 楼顶A的仰角为 (即 ),在多层洋房 的楼顶D处测得住宅楼 楼底B的俯角为 (即 ),已知 ,求高层住宅楼 的高度.(结果保留整数,测量工具的高度忽略不计.参考数据: , , , , , )
(1)、本次随机抽取的学生有名,等级为优秀(A)的学生人数所占的百分比是;(2)、在扇形统计图中,等级为合格(C)的学生所在扇形的圆心角度数是;(3)、将条形统计图补充完整;(4)、若该校九年级学生共1200名,请根据以上调查结果估算,等级为良好及良好以上的学生共有多少名?19. 北京冬奥会已落下帷幕,它惊艳了全世界,我国取得了9金4银2铜的历史最好成绩.本届奥运会有新星谷爱凌和苏翊鸣(分别用A,B表示)的诞生,也有老将徐梦桃和齐广璞(分别用C,D表示)的圆梦.为了传承并发扬奥运精神,某校开展“讲奥运冠军故事,传承奥运精神”的主题班会.(1)、小明从这四位奥运冠军中随机选取一位是谷爱凌的概率是;(2)、李亮小组从这四位奥运冠军中随机选取两位讲他们的故事,请用列表或面树状图的方法求李亮小组选取苏翊鸣和齐广璞的概率。20. 某社区为了创建干净整洁、和谐文明的社区环境,准备购买A,B两种分类垃圾桶,通过市场调研得知:A种垃圾桶每组的单价是B种垃圾桶每组单价的1.5倍,用7200元购买A种垃圾桶的组数比用6000元购买B种垃圾桶少5组.(1)、求A,B两种垃圾桶每组单价分别是多少元;(2)、该社区计划用不超过12000元的资金购买A,B两种垃圾桶共40组,则最多可以购买A种垃圾桶多少组?21. 某数学兴趣小组测量一栋高层住宅楼 的高度,在住宅楼 对面的多层洋房 的楼底C处,测得住宅楼 楼顶A的仰角为 (即 ),在多层洋房 的楼顶D处测得住宅楼 楼底B的俯角为 (即 ),已知 ,求高层住宅楼 的高度.(结果保留整数,测量工具的高度忽略不计.参考数据: , , , , , )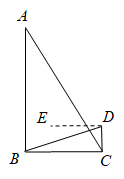 22. 如图,已知 内接于 , 为直径,D是 上一点,且 ,过点C作 交 的延长线于点E.
22. 如图,已知 内接于 , 为直径,D是 上一点,且 ,过点C作 交 的延长线于点E.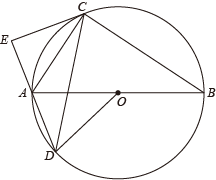 (1)、求证: 是 的切线;(2)、若 , ,求 的长.23. 某批发商以24元/箱的进价购进某种蔬菜,销往零售超市,已知这种蔬菜的标价为45元/箱,实际售价不低于标价的八折.批发商通过分析销售情况,发现这种蔬菜的日销售量y(箱)与当天的售价x(元/箱)满足一次函数关系,下表是其中的两组对应值.
(1)、求证: 是 的切线;(2)、若 , ,求 的长.23. 某批发商以24元/箱的进价购进某种蔬菜,销往零售超市,已知这种蔬菜的标价为45元/箱,实际售价不低于标价的八折.批发商通过分析销售情况,发现这种蔬菜的日销售量y(箱)与当天的售价x(元/箱)满足一次函数关系,下表是其中的两组对应值.售价x(元/箱)
…
35
38
…
销售量y(箱)
…
130
124
…
(1)、若某天这种蔬菜的售价为42元/箱,求当天这种蔬菜的销售量;(2)、若某天该批发商销售这种蔬菜获利1320元,则当天这种蔬菜的售价为多少元?(3)、批发商搞优惠活动,购买一箱这种蔬菜,赠送成本为6元的土豆,这种蔬菜的售价定为多少时,可获得日销售利润最大,最大日销售利润是多少元?24.(1)、【问题背景】
如图1,在正方形 中,E是 上一点,连接 ,F为射线 上一点(不与射线端点A重合),且 .求证: 且 ;
(2)、【类比探究】如图2,将(1)中的“正方形 ”改为“矩形 ”,其他条件均不变,若 , .探究线段 与 之间的关系,并说明理由;
(3)、【拓展延伸】在(2)的条件下,过点E作 交 于点H,延长 交 边于点G,若 是等腰三角形,直接写出 的值.
25. 如图,抛物线 交x轴于点A和 ,交y轴于点 ,D是抛物线的顶点.
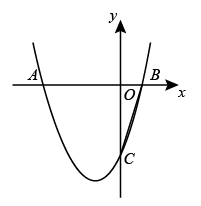 (1)、求抛物线的表达式和顶点D的坐标;(2)、E是线段 上一点,连接 , ,若 ,求点E的坐标;(3)、M是y轴上一动点,连接 并延长到点N,使 ,P是抛物线上一点,当 时,直接写出点P的横坐标
(1)、求抛物线的表达式和顶点D的坐标;(2)、E是线段 上一点,连接 , ,若 ,求点E的坐标;(3)、M是y轴上一动点,连接 并延长到点N,使 ,P是抛物线上一点,当 时,直接写出点P的横坐标