重庆市九龙坡区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-23 类型:期末考试
一、单选题
-
1. 下列各组线段能构成直角三角形的一组是( )A、 B、 C、 D、
-
2. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、
-
3. 一次函数 的图象和性质,叙述正确的是( )A、 随 的增大而增大 B、与 轴交于正半轴 C、与 轴交于正半轴 D、函数图象不经过第一象限
-
4. 二次根式 中 的取值范围是( )A、 B、 且 C、 D、 且
-
5. 已知某校八年级一班的张老师对上期组织的 次班级考试成绩进行比较分析,发现甲组同学的数学成绩比乙组同学的数学成绩要稳定些.现设甲,乙两组同学在上期 次数学考试成绩的方差分别为 ,则 与 大小关系为( )A、 B、 C、 D、不能确定
-
6. 如图,在平行四边形 中, 与 相交于点 ,则下列结论不一定成立的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 下列各曲线中,不表示 是 的函数的是( )A、
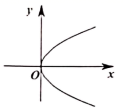 B、
B、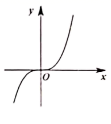 C、
C、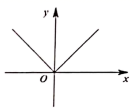 D、
D、
-
8. 某地区 年共 个月的每月的 的平均值如下图所示.则下列结论中错误的是( )
 A、 个月的 值不低于 的频率为 B、 个月的 值的平均值低于 C、 个月的 值的众数为 D、 个月的 值的中位数为
A、 个月的 值不低于 的频率为 B、 个月的 值的平均值低于 C、 个月的 值的众数为 D、 个月的 值的中位数为 -
9. 已知直线 与 轴, 轴分别交于 两点,在 轴上取一点 ,使得 是等腰三角形,则符合条件的点 有( )个A、 B、 C、 D、
-
10. 若 ,则 的值为( )A、 B、 C、 D、
-
11. 如图, 中,点 在边 上,以 为折痕,将 向上翻折,点 正好落在 上的点 处,若 的周长为 , 的周长为 ,则 的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12. 如图,矩形 的对角线相交于点 ,过点 作 ,交 于点 ,连接 ,若 ,则 的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
13. 计算: .
-
14. 已知正比例函数 的函数值 随 值的增大而增大,则一次函数 在平面直角坐标系内的图象经过第象限.
-
15. 如图,在菱形 中, 、 分别是 、 的中点,连接 .如果 ,那么 .

-
16. 某校举办广播体操比赛,评分项目包括精神面貌,整齐程度,动作规范这三项,总评成绩按以上三项得分 的比例计算,已知八( )班在比赛中三项得分依次是 分, 分, 分,则八( )班这次比赛的总成绩为分.
-
17. 甲、乙两名运动员在笔直的公路上进行骑自行车训练.如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程 (千米)与行驶时间 (小时)之间的关系,在两人行驶过程中,当 小时时,甲、乙两名运动员相距 千米.

-
18. 如图,点 为正方形 外一点, ,连接 ,过 作 于 ,直线 交于点 ,直线 交直线 于点 .结论:① ;② ;③ ;④ .则下列结论正确的是.(只填序号)

三、解答题
-
19. 计算:(1)、 .(2)、化简求值:已知 ,求 的值.
-
20. 如图, 为平行四边形 的对角线, 是 的中点, 是 的中点,连接 并延长交 于点 ,连接 G.
 (1)、求证: ;(2)、证明四边形 是菱形.
(1)、求证: ;(2)、证明四边形 是菱形. -
21. 请你用学习“一次函数和二次根式”时积累的经验和方法解决下列问题:(1)、在平面直角坐标系中,画出函数 的图象:
①列表填空:
②描点、连线,画出 的图象;
 (2)、结合所画函数图象,写出 两条不同类型的性质;(3)、结合所画函数图象,求方程 的解.
(2)、结合所画函数图象,写出 两条不同类型的性质;(3)、结合所画函数图象,求方程 的解. -
22. 在某学校组织的诗词比赛活动中,每个年级参加比赛的人数相同,成绩分为 、 、 、 四个等级,其中相应等级的赋分依次为 分, 分, 分, 分,该校发展处的陈主任将七年级和八年级的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
 (1)、此次竞赛中八年级成绩在 分及其以上的人数是人;(2)、求出下表中 、 、 的值:
(1)、此次竞赛中八年级成绩在 分及其以上的人数是人;(2)、求出下表中 、 、 的值:平均数(分)
中位数(分)
众数(分)
方差
七年级
八年级
(3)、学校准备在这两个年级中选一个年级参加市级诗词比赛,你建议学校选哪个年级参加最好?说说你的理由. -
23. 年春季我国武汉地区暴发的新型冠状病毒让口罩的需求量巨增.杨家坪某医药店准备购进一批防护口罩( )、医用护理口罩(以下依次简称为甲类口罩、乙类口罩),以购口罩的个数来计:二个甲类口罩和三个乙类口罩共需 元;三个甲类口罩和二个乙类口罩共需 元.(1)、求一个甲类口罩和一个乙类口罩的进价各是多少;(2)、若该医药店准备同时购进甲类、乙类这两种类型的口置共 个,且乙类口罩的数量不多于甲类口罩数量的 倍,请你设计出最省钱的购买方案,并说明理由.
-
24. 笛卡尔是法国数学家、科学家和哲学家.他的哲学与数学思想对历史的影响是深远的. 年,笛卡尔发表了《几何学》,创立了直角坐标系.其中笛卡尔的思想核心是:把几何学的问题归结成代数形式的问题,用代数的方法进行计算、证明,从而达到最终解决几何问题的目的.
小明在学习《勾股定理》时,利用平面直角坐标系在研究两点的距离时,通过数形结合发现(如图),平面内的任意两点 的距离,满足.经小明查阅资料得知,以上发现是成立的.在平面直角坐标系中, 叫 两点的距离公式.请你根据数形结合的思想和所学知识,完成以下问题:
 (1)、直接写出过 、 两点的距离为.(2)、写出点 到直线 的距离为.(3)、请求 ( 为任意实数)的最小值.
(1)、直接写出过 、 两点的距离为.(2)、写出点 到直线 的距离为.(3)、请求 ( 为任意实数)的最小值. -
25. 如图,在 中,点 为 上一点,过点 作 于点 于点 .连接 .
 (1)、若 ,求 的面积;(2)、若 ,求证: .
(1)、若 ,求 的面积;(2)、若 ,求证: . -
26. 如图 ,在平面直角坐标系中 为矩形, ,点 .直线 过点 、 .过点 作直线 交 轴于点 .
 (1)、求直线 的解析式;(2)、如图 ,点 、 分别为线段 、 上的动点,求 的最小值;(3)、如图 ,将 绕着原点 顺时针旋转 得到 ,旋转过程中直线 与直线 交于点 ,直线 与直线 交于点 .当 为等腰三角形时,请直接写出等腰 腰的长度及 的值.
(1)、求直线 的解析式;(2)、如图 ,点 、 分别为线段 、 上的动点,求 的最小值;(3)、如图 ,将 绕着原点 顺时针旋转 得到 ,旋转过程中直线 与直线 交于点 ,直线 与直线 交于点 .当 为等腰三角形时,请直接写出等腰 腰的长度及 的值.
(附参考数据:如图,在 中,若 ,则对应的边 )
