河北省石家庄市裕华区精英中学2016-2017学年中考数学模拟试卷
试卷更新日期:2017-10-26 类型:中考模拟
一、一.选择题:
-
1. 如图,数轴上的点A所表示的数为k,化简|k|+|1﹣k|的结果为( )
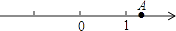 A、1 B、2k﹣1 C、2k+1 D、1﹣2k2. 若(x﹣2)(x2+ax+b)的积中不含x的二次项和一次项,则a和b的值( )A、a=0;b=2 B、a=2;b=0 C、a=﹣1;b=2 D、a=2;b=43. 下列四个图案中,属于中心对称图形的是( )A、
A、1 B、2k﹣1 C、2k+1 D、1﹣2k2. 若(x﹣2)(x2+ax+b)的积中不含x的二次项和一次项,则a和b的值( )A、a=0;b=2 B、a=2;b=0 C、a=﹣1;b=2 D、a=2;b=43. 下列四个图案中,属于中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 化简 的结果是( )A、 B、a C、a﹣1 D、5. 如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A﹣B﹣C﹣O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
4. 化简 的结果是( )A、 B、a C、a﹣1 D、5. 如图,已知矩形OABC,A(4,0),C(0,3),动点P从点A出发,沿A﹣B﹣C﹣O的路线勻速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )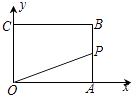 A、
A、 B、
B、 C、
C、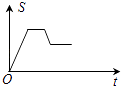 D、
D、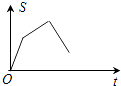 6. 任意四边形ABCD各边的中点分别是E,F,G,H,若对角线AC,BD的长都为20cm,则四边形EFGH的周长是( )A、80cm B、40cm C、20cm D、10cm7. 若代数式 有意义,则x的取值范围是( )A、x>1且x≠2 B、x≥1 C、x≠2 D、x≥1且x≠28.
6. 任意四边形ABCD各边的中点分别是E,F,G,H,若对角线AC,BD的长都为20cm,则四边形EFGH的周长是( )A、80cm B、40cm C、20cm D、10cm7. 若代数式 有意义,则x的取值范围是( )A、x>1且x≠2 B、x≥1 C、x≠2 D、x≥1且x≠28.如图,在一密闭的圆柱形玻璃杯中装一半的水,水平放置时,水面的形状是( )
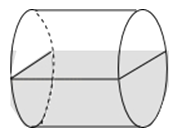 A、圆 B、长方形 C、椭圆 D、平行四边形9. 如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )
A、圆 B、长方形 C、椭圆 D、平行四边形9. 如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )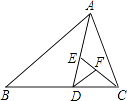 A、12 B、14 C、16 D、1810. 如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )
A、12 B、14 C、16 D、1810. 如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( ) A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:511. 如图,数轴上点M所表示的数可能是( )
A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:511. 如图,数轴上点M所表示的数可能是( )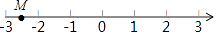 A、1.5 B、﹣1.6 C、﹣2.6 D、﹣3.412. 某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件才能按时交货,则x应满足的方程为( )A、 B、 = C、 D、13. 由线段a、b、c组成的三角形不是直角三角形的是( )A、a=7,b=24,c=25 B、a= ,b=4,c=5 C、a= ,b=1,c= D、a= ,b= ,c=14. 关于x的一元二次方程ax2﹣x+1=0有实数根,则a的取值范围是( )
A、1.5 B、﹣1.6 C、﹣2.6 D、﹣3.412. 某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件才能按时交货,则x应满足的方程为( )A、 B、 = C、 D、13. 由线段a、b、c组成的三角形不是直角三角形的是( )A、a=7,b=24,c=25 B、a= ,b=4,c=5 C、a= ,b=1,c= D、a= ,b= ,c=14. 关于x的一元二次方程ax2﹣x+1=0有实数根,则a的取值范围是( )
A、a≤ 且a≠0 B、a≤ C、a≥ 且a≠0 D、a≥15. 如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )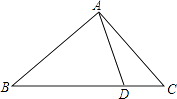 A、AC:BC=AD:BD B、AC:BC=AB:AD C、AB2=CD•BC D、AB2=BD•BC16. 矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
A、AC:BC=AD:BD B、AC:BC=AB:AD C、AB2=CD•BC D、AB2=BD•BC16. 矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )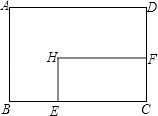 A、
A、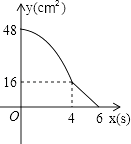 B、
B、 C、
C、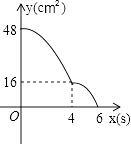 D、
D、
二、填空题:
-
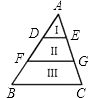
17. 一个数的立方根是4,那么这个数的平方根是 .18. 分解因式:x2﹣4(x﹣1)= .19. 如图,AD=DF=FB,DE∥FG∥BC,则SⅠ:SⅡ:SⅢ= .
三、解答题
-
20. 计算:
(1)、(﹣2)3÷ +3×|1﹣(﹣2)2|
(2)、﹣12﹣( ﹣ )÷ ×[﹣2+(﹣3)2].21. 如图,点A,B,C,D在一条直线上,△ABF≌△DCE.你能得出哪些结论?(请写出三个以上的结论) 22. 已知,如图,△ABC是正三角形,D,E,F分别是各边上的一点,且AD=BE=CF.请你说明△DEF是正三角形.
22. 已知,如图,△ABC是正三角形,D,E,F分别是各边上的一点,且AD=BE=CF.请你说明△DEF是正三角形.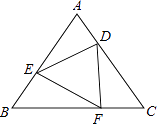 23. 某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:
23. 某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图: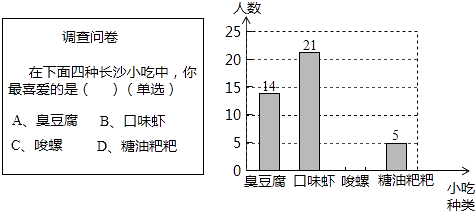
请根据所给信息解答以下问题:
(1)、请补全条形统计图;(2)、若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?(3)、在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.24. A市和B市分别有库存的某联合收割机12台和6台,现决定开往C市10台和D市8台,已知从A市开往C市、D市的油料费分别为每台400元和800元,从B市开往C市和D市的油料费分别为每台300元和500元.(1)、设B市运往C市的联合收割机为x台,求运费w关于x的函数关系式.
(2)、若总运费不超过9000元,问有几种调运方案?
(3)、求出总运费最低的调运方案,并求出最低运费.25. 如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)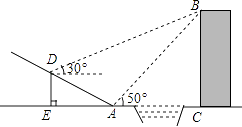 26. 如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
26. 如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米. (1)、求y1与x的函数关系,并在图2中画出y1的图象;(2)、如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;(3)、在图2中,点G是x轴正半轴上一点0<OG<6,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.
(1)、求y1与x的函数关系,并在图2中画出y1的图象;(2)、如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;(3)、在图2中,点G是x轴正半轴上一点0<OG<6,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.