天津市南开区2020年中考数学二模试卷
试卷更新日期:2020-07-14 类型:中考模拟
一、单选题
-
1. 计算 的结果是( )A、6 B、12 C、-12 D、-3
-
2. 的值等于( )A、 B、 C、3 D、1
-
3. 5月18日,我市新一批复课开学共涉及全市877所小学、489所中学,63万名中小学生.将“63万”用科学记数法表示为( )A、 B、 C、 D、
-
4. 下列常用手机 APP 的图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
5. 如图是由多个相同小立方体搭成的几何体的三视图,则这个几何体是( )
 A、
A、 B、
B、 C、
C、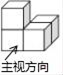 D、
D、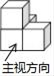
-
6. 已知 ,估计m的值在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间
-
7. 化简 的结果是( )A、 B、 C、 D、
-
8. 方程组 的解是( )A、 B、 C、 D、
-
9. 若点 , , 在反比例函数 ( 为常数)的图象上,则 , , 的大小关系是( )A、 B、 C、 D、
-
10. 如图,五边形 是 的内接正五边形, 是 的直径,则 的度数是( )
 A、18° B、36 C、 D、72°
A、18° B、36 C、 D、72° -
11. 如图,在 中, , ,点 在边 上,且 ,点 为 的中点,点 为边 上的动点,当点 在 上移动时,使四边形 周长最小的点 的坐标为( )
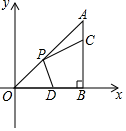 A、 B、 C、 D、
A、 B、 C、 D、 -
12. 二次函数 的图象如图所示,对称轴是直线 .下列结论:① ;② ;③ ;④ ( 为实数).其中结论正确的个数为( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个
二、填空题
-
13. 把多项式x3﹣25x分解因式的结果是
-
14. 计算 的结果等于.
-
15. 已知直线 与两坐标轴分别交于A , B两点,线段 的长为.
-
16. 在学校组织的朗诵比赛中,甲、乙两名学生以抽签的方式从3篇不同的文章中抽取篇参加比赛,抽签规则是:在3个相同的标签上分别标注字母A、B、C , 各代表1篇文章,一名学生随机抽取一个标签后放回,另一名学生再随机抽取.则甲、乙抽中同一篇文章的概率为.
-
17. 如图,在平面直角坐标系xOy中,直线 经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°,得到△CBD,若点B的坐标为(4,0),则点C的坐标为.
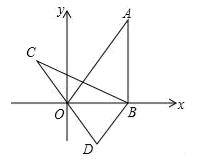
-
18. 如图,在每个小正方形的边长为1的网格中,A , B , D , E为格点,C为 , 的延长线的交点.
 (1)、 的结果为.(2)、若点R在线段 上,点S在线段 上,点T在线段 上,且满足四边形 为菱形,请在如图所示的网格中,用无刻度的直尺,画出菱形 ,并简要说明点R , S , T的位置是如何找到的(不要求证明)
(1)、 的结果为.(2)、若点R在线段 上,点S在线段 上,点T在线段 上,且满足四边形 为菱形,请在如图所示的网格中,用无刻度的直尺,画出菱形 ,并简要说明点R , S , T的位置是如何找到的(不要求证明)
三、解答题
-
19. 解不等式组
请结合题意填空,完成本题的解答.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来: (4)、原不等式组的解集为.
(4)、原不等式组的解集为. -
20. 某校350名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成了图1和图2两个统计图表.

请根据相关信息回答下列问题:
(1)、此次共随机抽查了名学生每人的植树量;图①中m的值为;
(2)、求统计的这组数据的平均数、众数和中位数;(3)、根据样本数据,估计这350名学生共植树多少棵? -
21. 如图1, 是 的直径,弦 于G , 过C点的切线与射线 相交于点E , 直线 与 交于点H , , .
 (1)、求 的半径;(2)、将射线 绕D点逆时针旋转,得射线 (如图2), 与 交于点M , 与 及切线 分别相交于点N , F , 当 时,求切线 的长.
(1)、求 的半径;(2)、将射线 绕D点逆时针旋转,得射线 (如图2), 与 交于点M , 与 及切线 分别相交于点N , F , 当 时,求切线 的长. -
22. 某数学社团成员想利用所学的知识测量某广告牌的宽度(图中线段MN的长),直线MN垂直于地面,垂足为点P . 在地面A处测得点M的仰角为58°、点N的仰角为45°,在B处测得点M的仰角为31°,AB=5米,且A、B、P三点在一直线上.请根据以上数据求广告牌的宽MN的长.
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60,sin31°=0.52,cos31°=0.86,tan31°=0.60.)

-
23. 某市中心城区居民用水实行以户为单位的三级阶梯收费办法:
第Ⅰ级:居民每户每月用水不超过18吨时,每吨收水费3元;
第Ⅱ级:居民每户每月用水超过18吨但不超过25吨,未超过18吨的部分按照第Ⅰ级标准收费,超过的部分每吨收水费4元;
第Ⅲ级:居民每户每月用水超过25吨,未超过25吨的部分按照第Ⅰ、Ⅱ级标准收费,超过的部分每吨收水费6元.
现把上述水费阶梯收费办法称为方案①;假设还存在方案②:居民每户月用水一律按照每吨4元的标准缴费.
设一户居民月用水x吨.
(1)、根据题意填表: (2)、设方案①应缴水费为 元,方案②应缴水费为 元,分别求 , 关于x的函数解析式;(3)、当 时,通过计算说明居民选择哪种付费方式更合算.
(2)、设方案①应缴水费为 元,方案②应缴水费为 元,分别求 , 关于x的函数解析式;(3)、当 时,通过计算说明居民选择哪种付费方式更合算. -
24. 如图,在平面直角坐标系中,四边形 是矩形,点 ,点 ,点 ;D为 边上的动点.
 (1)、如图1,将 对折,使得点B的对应点 落在对角线 上,折痕为 ,求此刻点D的坐标;(2)、如图2,将 对折,使得点A的与点C重合,折痕交 于点D , 交 于点E , 求直线 的解析式;(3)、在坐标平面内,是否存在点P(除点B外),使得 与 全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)、如图1,将 对折,使得点B的对应点 落在对角线 上,折痕为 ,求此刻点D的坐标;(2)、如图2,将 对折,使得点A的与点C重合,折痕交 于点D , 交 于点E , 求直线 的解析式;(3)、在坐标平面内,是否存在点P(除点B外),使得 与 全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由. -
25. 如图,在平面直角坐标系中,已知点B的坐标为 ,且 ,抛物线 图象经过 三点.
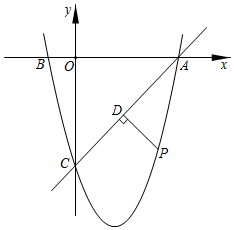 (1)、求 两点的坐标;(2)、求抛物线的解析式;(3)、若点 是直线 下方的抛物线上的一个动点,作 于点 ,当 的值最大时,求此时点 的坐标及 的最大值.
(1)、求 两点的坐标;(2)、求抛物线的解析式;(3)、若点 是直线 下方的抛物线上的一个动点,作 于点 ,当 的值最大时,求此时点 的坐标及 的最大值.
