贵州省安顺市2019-2020学年高三上学期理数第一次联考试卷
试卷更新日期:2019-12-20 类型:高考模拟
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、
-
2. ( )A、 B、 C、 D、
-
3. 2019年篮球世界杯中,两位队员每场比赛得分的茎叶图如图所示,若甲得分的众数是18,乙得分的中位数是15,则 ( )
 A、 15 B、8 C、13 D、33
A、 15 B、8 C、13 D、33 -
4. 已知向量 , ,则 ( )A、7 B、8 C、 D、9
-
5. 已知 ,则( )A、 B、 C、 D、
-
6. 已知函数 的导函数为 ,且 ,则 ( )A、2 B、3 C、4 D、5
-
7. 执行下面的程序框图,若输入的 ,则输出的 的值为( )
 A、7 B、-17 C、31 D、-65
A、7 B、-17 C、31 D、-65 -
8. 某几何体的三视图如图所示,则该几何体的体积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9. 已知函数 ,要得到 的图象,只需将 的图象( )A、向左平移 个单位长度 B、向右平移 个单位长度 C、向右平移 个单位长度 D、向左平移 个单位长度
-
10. 如图,在正方形 中, 分别是 的中点, 是 的中点.现在沿 及 把这个正方形折成一个空间图形,使 三点重合,重合后的点记为 ,下列说法:
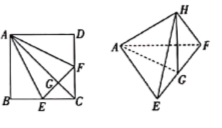
① 平面 ;② 平面 ;
③ 平面 ;④ 平面 .
其中正确的有( )
A、1个 B、2个 C、3个 D、4个 -
11. 如图,正方体 的棱长为 , 为 的中点,动点 从点 出发,沿 运动,最后返回 .已知 的运动速度为 ,那么三棱锥 的体积 (单位: )关于时间 (单位: )的函数图象大致为( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
12. 已知函数 ,若 ,则 的取值范围是( )A、 B、 C、 D、
二、填空题
-
13. 某学校高一、高二、高三年级的学生人数成等差数列,现用分层抽样的方法从这三个年级中抽取90人,则应从高二年级抽取的学生人数为.
-
14. 过直线 上的任意一点作圆 的切线,则切线长的最小值为.
-
15. 五个同学重新随机调换座位,则恰有两人坐在自己原来的位置上的概率为.
-
16. 已知三棱锥 满足平面 平面 , , , ,则该三棱锥的外接球的表面积为.
三、解答题
-
17. 某研究机构为了解某学校学生使用手机的情况,在该校随机抽取了60名学生(其中男、女生人数之比为2:1)进行问卷调查.进行统计后将这60名学生按男、女分为两组,再将每组学生每天使用手机的时间(单位:分钟)分为 5组,得到如图所示的频率分布直方图(所抽取的学生每天使用手机的时间均不超过50分钟).
 (1)、求出女生组频率分布直方图中 的值;(2)、求抽取的60名学生中每天使用手机时间不少于30分钟的学生人数.
(1)、求出女生组频率分布直方图中 的值;(2)、求抽取的60名学生中每天使用手机时间不少于30分钟的学生人数. -
18. 在 中,角 的对边分别为 , .(1)、求 的值;(2)、求 的值.
-
19. 已知数列 的前 项和为 ,且 .(1)、求 的通项公式;(2)、若 ,求数列 的前 项和 .
-
20. 如图,在三棱锥 中, ,二面角 的大小为120°,点 在棱 上,且 ,点 为 的重心.
 (1)、证明: 平面 ;(2)、求二面角 的正弦值.
(1)、证明: 平面 ;(2)、求二面角 的正弦值. -
21. 已知函数 .(1)、当 时,不等式 恒成立,求实数 的取值范围;(2)、证明: , .
-
22. 在直角坐标系 中,直线 的参数方程为 (其中 为参数).以坐标原点 为极点, 轴非负半轴为极轴建立极坐标系,曲线 的极坐标方程为 .(1)、求 和 的直角坐标方程;(2)、设点 ,直线 交曲线 于 两点,求 的值.
-
23. 已知函数 .(1)、求不等式 的解集;(2)、若 的解集包含 ,求实数 的取值范围.
