-
1、若式子在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、
-
2、如图,在下列四组条件中,能证明的条件是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、下列计算正确的是( )A、 B、 C、 D、
-
4、甲骨文是我国的一种古代文字,下列甲骨文中,能用其中一部分平移得到的是( )A、
 B、
B、 C、
C、 D、
D、
-
5、【阅读理解】我们在分析和解决某些数学问题时,经常要比较两个数或代数式的大小,解决问题的策略一般都是进行一定的转化,其中“作差法”就是常用的方法之一,作差法就是通过作差、变形,利用差的符号确定它们的大小,即要比较代数式A,B的大小,只要计算的值,若 , 则;若 , 则;若 , 则 .
【知识运用】用上述方法,解决以下问题:
(1)比较大小: ___________ .
(2)当时,比较与的大小,并说明理由.
【解决问题】
(3)图①是边长为4的正方形,将正方形一组对边保持不变,另一组对边增加得到如图②所示的长方形,此长方形的面积为;将正方形的边长增加a,得到如图③所示的大正方形,此时大正方形的面积为 .

①请判断与的大小关系,并说明理由;
②已知 , 则A与B的大小关系为:A___________B.
-
6、如图,直线 , 直线c与直线a,b分别相交于点A,B,点D为直线a上一点(位于点A的右侧), . 平分 , 交直线b于点C,把三角形沿着平行线向右平移得到三角形 .
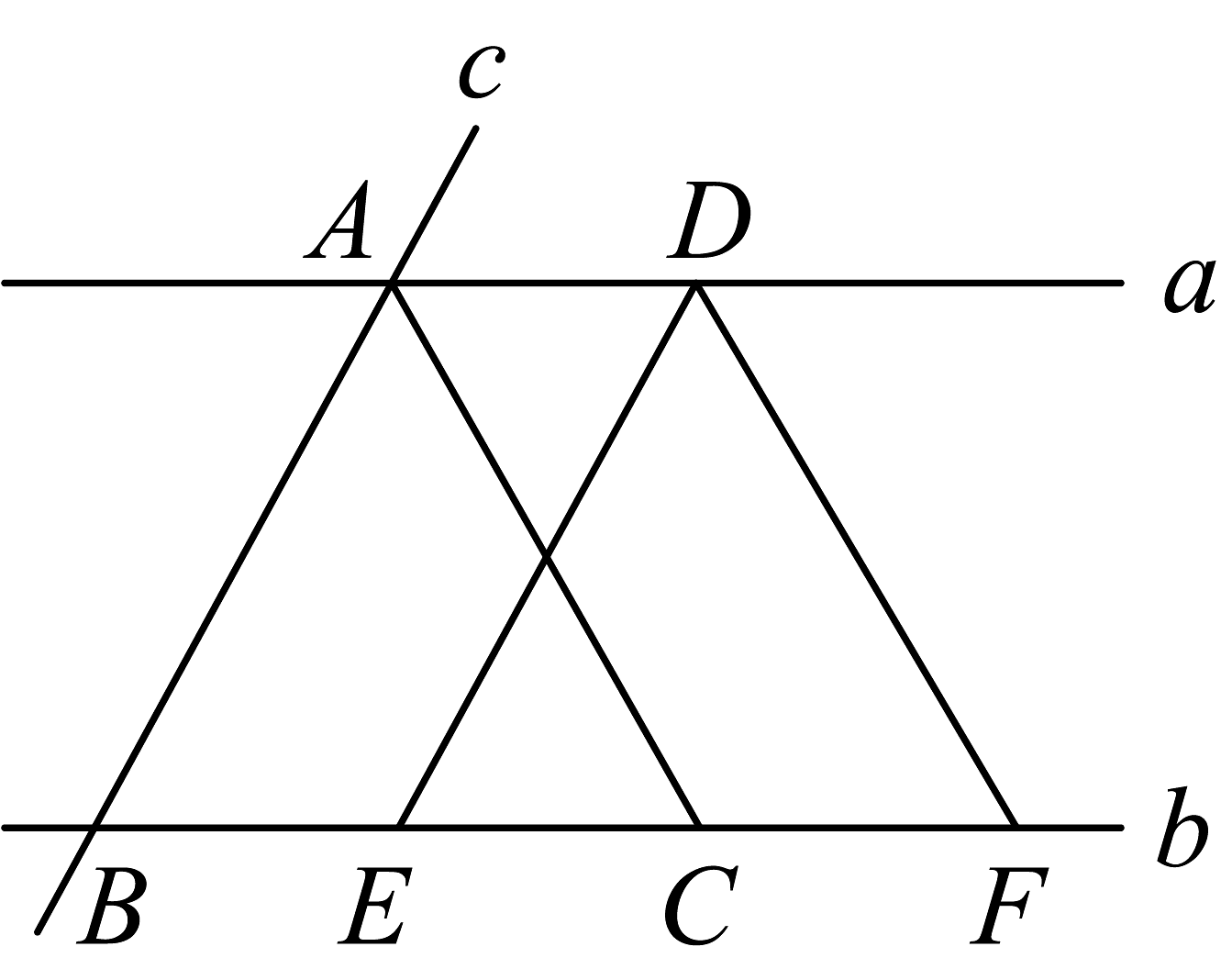 (1)、请说明;(2)、若三角形的周长是 , 求四边形的周长.
(1)、请说明;(2)、若三角形的周长是 , 求四边形的周长. -
7、如图,方格纸中每个小正方形的边长都是1,三角形的三个顶点都在格点上.在方格纸内将三角形经过一次平移后得到三角形 , 图中标出了点A的对应点 .
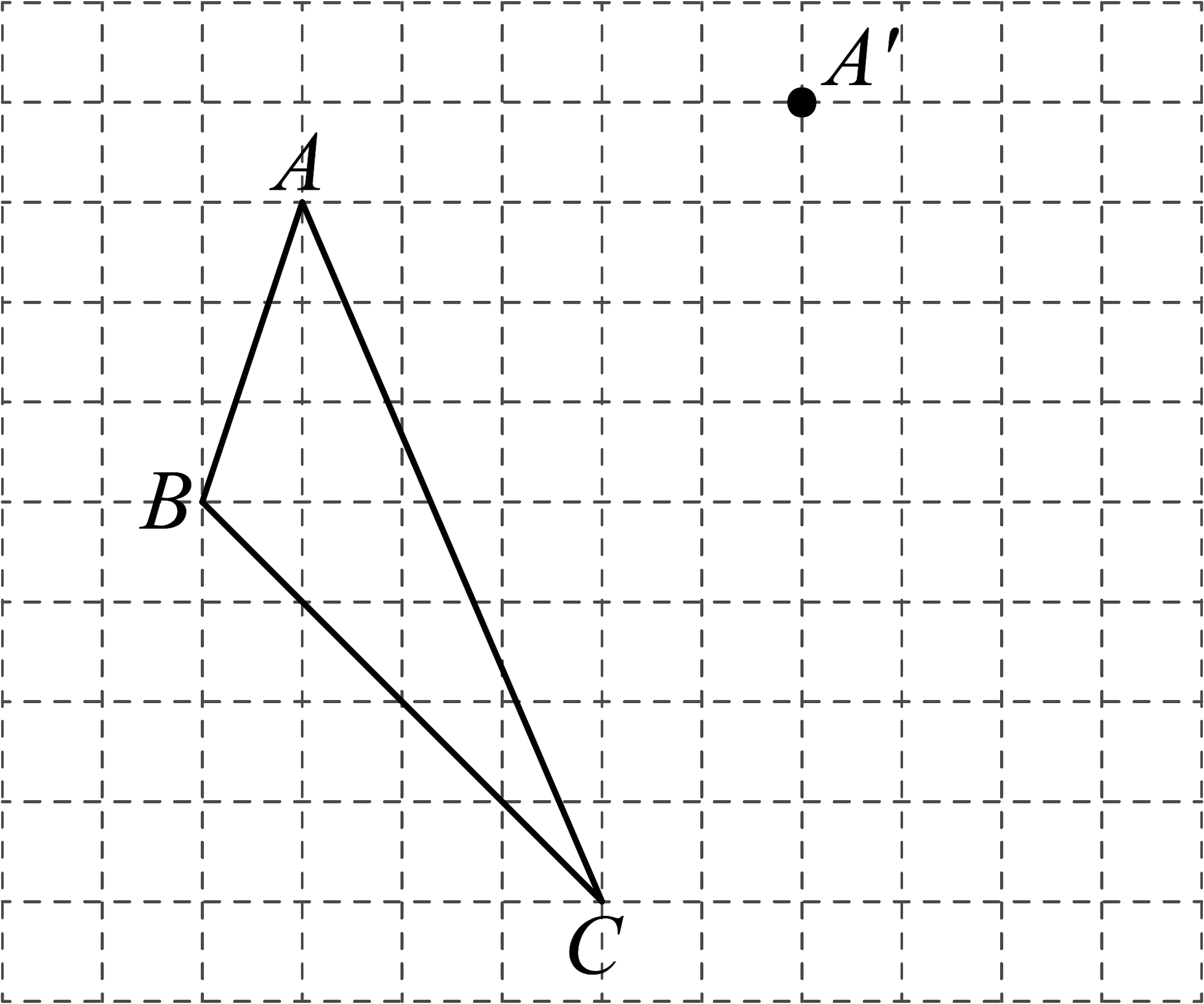 (1)、在图中画出平移后的三角形;(2)、线段和的数量关系是;(3)、过点B画出线段的垂线段交于点D.
(1)、在图中画出平移后的三角形;(2)、线段和的数量关系是;(3)、过点B画出线段的垂线段交于点D. -
8、(1)计算:
(2)先化简,再求值: , 其中 .
-
9、某种春季流感病毒的直径约为米,该直径用科学记数法表示为米.
-
10、某单位为一中学捐赠了一批新桌椅,学校组织七年级200名学生搬桌椅.规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅的套数(一桌一椅为一套)为( )A、81套 B、80套 C、79套 D、75套
-
11、若关于x的不等式组的解集为 , 则的值为( )A、 B、1 C、 D、3
-
12、因式分解 , 结果正确的是( )A、 B、 C、 D、
-
13、下列运算正确的是( )A、 B、 C、 D、
-
14、如图所示,点A到BC所在的直线的距离是指图中线段( )的长度.
 A、AC B、AF C、BD D、CE
A、AC B、AF C、BD D、CE -
15、下列四个汽车标志中,能用平移得到的是( )A、
 B、
B、 C、
C、 D、
D、
-
16、如图1,已知正方形中,是边上的一点(不与 , 重合).延长至点使 , 连接 , 得到 , 的延长线交于点 .
 (1)、①求证:;
(1)、①求证:;②求的度数.
(2)、如图2,连接 , .①求证:;
②求的值
-
17、如果关于的一元二次方程有两个实数根,且其中一个根是另一个根的倍为正整数),则称这样的方程为“倍根方程”.例如:方程的两个根分别是2和4,则这个方程就是“二倍根方程”;方程的两个根分别是1和3,则这个方程就是“三倍根方程”.(1)、根据上述定义,是“________倍根方程”;(2)、若关于的方程是“三倍根方程”,求的值;(3)、直线:与轴交于点 , 直线过点 , 且与相交于点 . 若一个五倍根方程的两个根为和 , 且点在的内部(不包含边界),求的取值范围.
-
18、为迎接湖南师大附中梅溪湖中学办学十周年庆,某校友为母校设计了一款纪念版文化衫,原计划每件的售价为元,经过校友意见征集后,连续两次降价,最终每件的售价为元,并且每次降价的百分率相同.(1)、求该文化衫每次降价的百分率;(2)、若该文化衫每件的成本价为元,两次降价后,至少要售出多少件,总利润才能不低于元?
-
19、如图,在四边形中, , , 对角线 , 相交于点 .
 (1)、求证:四边形是平行四边形;(2)、若 , , , 求的长
(1)、求证:四边形是平行四边形;(2)、若 , , , 求的长 -
20、如图,在平面直角坐标系中,一直线与轴相交于点 , 与轴相交于点 , 与正比例函数的图象交于点 .
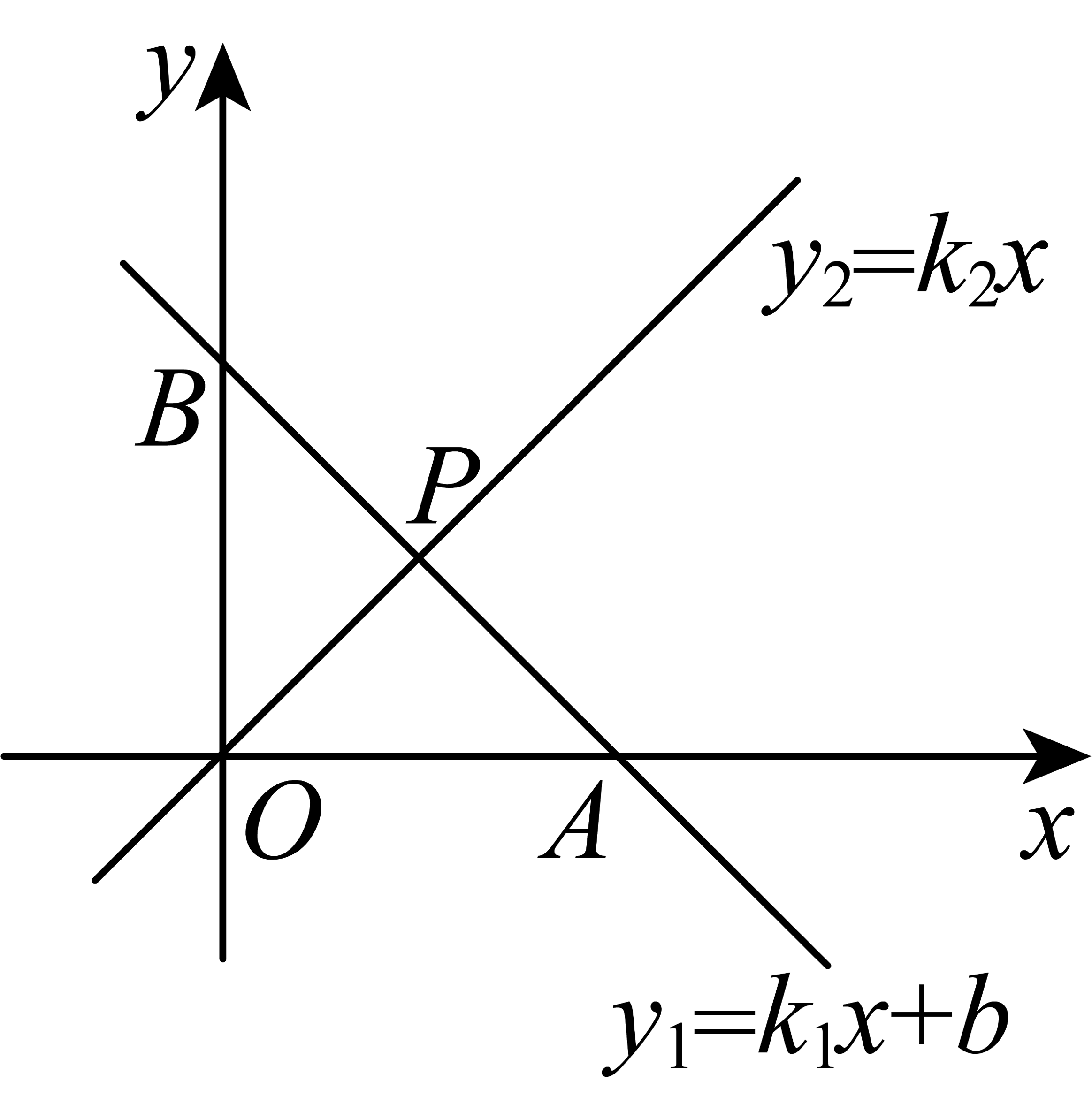 (1)、求直线的解析式.(2)、直接写出的解集.
(1)、求直线的解析式.(2)、直接写出的解集.