-
1、 计算:
-
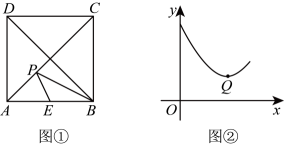
2、 如图①,在正方形中,点是的中点,点是对角线上一动点,设 , , 图②是关于的函数图象,且图象上最低点的坐标为 , 则正方形的边长为 .
-
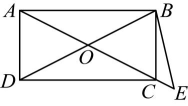
3、 如图,在四边形中, , 且 , , 点、分别从点、同时出发,点以的速度由点向点运动,点以的速度由点向点运动,当点、中有一点到达终点时,另一点也随之停止运动,则后四边形是平行四边形.

-
4、 反比例函数 的图像如图所示,若的面积是3,则k 的值为 .
-
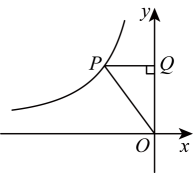
5、 如图,点是矩形的对角线的延长线上一点,若 , , 则 .
-
6、 已知关于的分式方程有增根,则的值是 .
-
7、 点在第象限.
-
8、 在函数中,自变量的取值范围是 .
-
9、 如图,在正方形中,点在对角线上,连接 , 过点作的垂线交于点 , 交的延长线于点 , 若点是的中点, , 则的长度为( )
 A、4 B、5 C、 D、
A、4 B、5 C、 D、 -
10、 如图,在菱形中,对角线 , 相交于点 , 交于点 , 若 , , 则的长为( )
 A、2 B、 C、 D、
A、2 B、 C、 D、 -
11、 关于x的函数和 , 它们在同一坐标系内的图像大致是( )A、
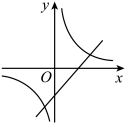 B、
B、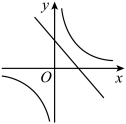 C、
C、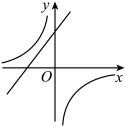 D、
D、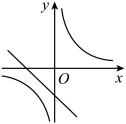
-
12、 在古代建筑中,榫(sǔn)卯(mǎo)结构至关重要,它通过凸出的榫和凹进的卯精密配合连接,使得建筑物连接牢固且难以松动.工匠们制作了一种特定的榫卯组合,每个榫需要的木材比每个卯需要的木材多千克.已知用30千克木材制作榫的数量与用25千克木材制作卯的数量相同.设制作1个榫需要的木材为x千克,则符合题意的方程是( )A、 B、 C、 D、
-
13、 如图,在中, , 的平分线交于点 , 则的长为( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
14、 解分式方程 , 去分母得( )A、 B、 C、 D、
-
15、 若分式的值等于0,则x的值为( )A、﹣1 B、0 C、1 D、±1
-
16、 如图,这是某绿色植物的细胞结构图,该绿色植物细胞的直径约为0.000009米,将数据0.000009用科学记数法表示为( )
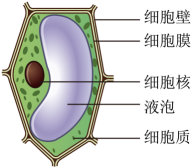 A、 B、 C、 D、
A、 B、 C、 D、 -
17、 已知点、点 , 若满足点 , 则称点A、B关于点对称;若函数图象上所有点关于点对称的点均在函数的图象上,则称函数与函数关于点对称.(1)、已知点 , 则点A关于原点、关于点的对称点的坐标分别是 , , 关于点对称的点的坐标是(用含a、b的式子表示);(2)、已知抛物线:与抛物线:关于点R对称,抛物线的顶点为M , 若将点M向右平移2个单位,再向下平移1个单位,得到的点 , 恰好在抛物线上,求点R的坐标;(3)、已知抛物线:关于点对称的抛物线为 , 当时,抛物线的最大值和最小值之差为3,求m的值.
-
18、 定义:已知直线l:(k为常数)绕定点旋转,则称直线l为“旋转簇直线”,点为“旋转簇直线”的不动点,
 (1)、求直线l:的不动点坐标;(2)、已知直线:与x、y轴分别交于点A、B .
(1)、求直线l:的不动点坐标;(2)、已知直线:与x、y轴分别交于点A、B .①如图1,直线l:(k为常数)绕不动点P旋转时,与y轴正半轴相交于点Q , 且点Q在点B上方,当时,求点Q坐标;
②如图2,直线与x正半轴交于点C , 与直线相交于第一象限内的点D , 且恒有 , 试问直线是否为“旋转簇直线”,若是,请求出不动点的坐标;若不是,请说明理由.
-
19、 如图,在矩形中,已知 , 点E、F分别为、上两点,连接、 .
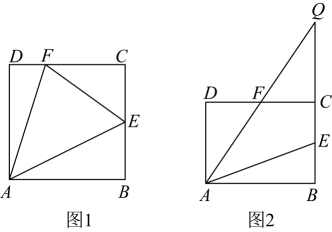 (1)、如图1,当时,连接 , 且 .
(1)、如图1,当时,连接 , 且 .①已知 , , 求的长;
②已知 , 求的值;
(2)、如图2,若平分 , 且 , 延长交延长线于点Q , 若 , , 求k的值. -
20、 某地2023年种植黄桃100亩,由于效益不错,每年都在扩大种植面积,到2025年种植了121亩.(1)、假定每年种植面积的年增长率相同,求种植黄桃亩数的年平均增长率;(2)、一水果店以每件20元的价格购进该种黄桃销售,市场调查发现,黄桃每天的销售量y(件)与销售单价x(元/件)之间满足一次函数关系,部分数据如表:
销售单价x(元)
22
24
27
销售量y(件)
200
180
150
①求y与x之间的函数关系式,并直接写出自变量的取值范围;
②若要使每天的销售利润最大,销售单价应定为多少元,每天能获得的最大销售利润是多少元?