-
1、 立定跳远是初中体育课程中的一项,为了解七年级学生立定跳远成绩的情况,某校体育组随机抽取了部分学生的跳远成绩(单位:米)进行处理分析,制成频数分布图表如下:
成绩/米
频数
百分数
6
30
48
18
6

根据表中提供的信息解答下列问题:
(1)、 , ;(2)、补全频数分布直方图;(3)、已知七年级有800名学生参加立定跳远测试,请估计该年级立定跳远成绩为优秀(1.7米以上)的人数. -
2、 三角形ABC在平面直角坐标系中的位置如图所示,将图中三角形ABC向左平移3个单位长度,再向下平移2个单位长度,得到三角形 .
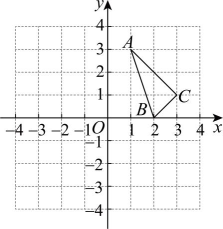 (1)、请在图中画出三角形 , 并写出下列各点的坐标: _▲ , B' _▲ ;(2)、计算三角形的面积.
(1)、请在图中画出三角形 , 并写出下列各点的坐标: _▲ , B' _▲ ;(2)、计算三角形的面积. -
3、 解不等式(组):(1)、(2)、
-
4、 解方程组:
-
5、 计算: .
-
6、 已知关于x的不等式组有解,则实数a的取值范围是 .
-
7、 如图,A和B的坐标为(2,0),(0,1),若将线段AB平移至 , 则ab的值为 .

-
8、 已知、满足方程组 , 则的值为 .
-
9、 对于 , 符号 表示不大于的最大整数,如 , , 则满足关系式的的整数值的个数是( )A、个 B、个 C、个 D、个
-
10、 现用186张铁皮做盒子,每张铁皮可做8个盒身或15个盒底,且一个盒身与两个盒底配成一个盒子.设用x张铁皮做盒身,y张铁皮做盒底,则可得方程组( )A、 B、 C、 D、
-
11、 在平面直角坐标系中,第一象限内的点距离轴个单位长度,则的值为( )A、 B、或 C、 D、
-
12、 如图,点在的延长线上,下列条件中,能判断的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、 下列调查中,适合抽样调查的是( )A、了解某校七年(1)班学生校服的尺码情况 B、检测一批LED灯的使用寿命 C、某公司对参加招聘的人员进行面试 D、检查锦州湾机场搭乘某航班的旅客是否携带违禁物品
-
14、 的相反数是( )A、2 B、-2 C、4 D、-4
-
15、 在平面内,为线段外的一点,若以 , , 为顶点的三角形为直角三角形,则称为线段的直角点.特别地,当该三角形为等腰直角三角形时,称为线段的等腰直角点.
 (1)、如图1,在平面直角坐标系中,点的坐标为 , 在点 , , 中,线段的直角点是;(2)、在平面直角坐标系中,点 , 的坐标分别为 , , 直线l的解析式为 .
(1)、如图1,在平面直角坐标系中,点的坐标为 , 在点 , , 中,线段的直角点是;(2)、在平面直角坐标系中,点 , 的坐标分别为 , , 直线l的解析式为 .①如图2,是直线上的一个动点,若是以线段为直角边的直角点,求点的坐标;
②点是直线上的一个动点,将所有线段的等腰直角点称为直线关于点的伴随点.若某正方形的中心(对角线的交点)为原点 , 它的各边分别与两坐标轴平行,且该正方形上恰有两个点为直线关于点的伴随点,求出正方形边长的取值范围.
-
16、 如图,点和是一次函数的图象与反比例函数的图象的两个交点,直线交轴于点 .
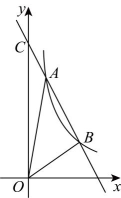 (1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、设点是坐标平面内一个动点,点在轴上运动,当以点 , , , 为顶点的四边形是菱形时,请直接写出点的坐标.
(1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、设点是坐标平面内一个动点,点在轴上运动,当以点 , , , 为顶点的四边形是菱形时,请直接写出点的坐标. -
17、 “雨过园亭绿暗时,樱桃红颗压枝低”.2024年青岛樱桃节期间,张大爷购进了一批质量相等的大小樱桃,已知每千克小樱桃的进价比每千克大樱桃少8元.受污损的进货清单如表所示:
品名
大樱桃
小樱桃
进价/(元/千克)


总价/元
1134
630
(1)、请你帮张大爷求出每千克大樱桃和小樱桃的进价各是多少元.(2)、若张大爷决定再次购进同种大樱桃和小樱桃共60千克,再次购进的费用不超过1000元,若每种樱桃的进价保持不变,大樱桃的销售单价为30元,小樱桃的销售单价为18元,张大爷应如何进货,才能使第二批大樱桃和小樱桃售完后获得最大利润?(3)、利润关系仍然满足(2)中的利润关系,张大爷推出福利活动,决定拿出销售利润的另购大、小樱桃赠送游客免费品尝,第二批购进大樱桃至少多少千克,能使剩余利润不少于450元? -
18、 如图,在中,点是边的中点,连接并延长,交的延长线于点 . 连接、 .
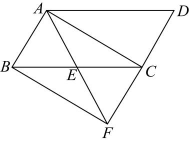 (1)、求证:;(2)、当时,请判断四边形的形状,并说明理由.
(1)、求证:;(2)、当时,请判断四边形的形状,并说明理由. -
19、 西安市2024年中考,综合素质测试满分为100分.某校为了调查学生对于综合素质的掌握程度,在九年级学生中随机抽取了部分学生进行模拟测试,并将测试成绩绘制成下面两幅统计图.试根据统计图中提供的数据,回答下面问题:
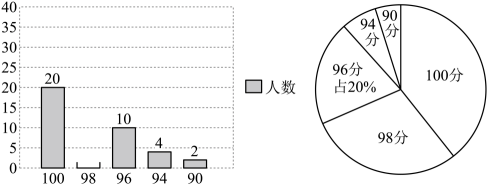 (1)、本次调查的学生人数共有 人,并补全条形统计图.(2)、样本中,测试成绩的中位数是分,众数是分.(3)、若该校九年级共有2000名学生,根据此次模拟成绩估计该校九年级中考综合速度测试将有多少名学生可以获得满分.
(1)、本次调查的学生人数共有 人,并补全条形统计图.(2)、样本中,测试成绩的中位数是分,众数是分.(3)、若该校九年级共有2000名学生,根据此次模拟成绩估计该校九年级中考综合速度测试将有多少名学生可以获得满分. -
20、 先化简,再求值: , 其中 .