-
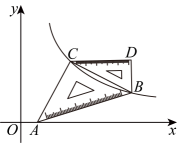
1、在平面直角坐标系中,一副三角尺如图放置, , 点在轴的正半轴上,点、在反比例函数的图象上.若轴, , 则的值为 .
-
2、某网店某种商品成本为50元/件,售价为60元/件时,每天可销售100件;售价单价高于60元时,每涨价1元,日销售量就减少2件.据此,当销售单价为元时,网店该商品每天盈利最多.
-
3、若点与点关于坐标原点对称,则的值为 .
-
4、已知一样本数据4,4,5,6,的平均数为5,则数的值为 .
-
5、一个正多边形的每个外角都等于 , 那么它是边形.
-
6、如图,在正方形中,对角线、交于点 , 延长到 , 连结 , 过点作 , 分别交、于点、 , 连结 , 则下面哪个图形的面积与的面积相等( )
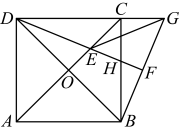 A、四边形 B、 C、四边形 D、
A、四边形 B、 C、四边形 D、 -
7、反比例函数的图像上有 , 两点,下列判断正确的是( )A、当时, B、当且时, C、当时, D、当且时,
-
8、在菱形中, , 点、分别在边、上,连结、 , 则添加下列条件后,不能判定的是( )A、 B、 C、 D、
-
9、若关于的一元二次方程有两个相等的实数根,则的值是( )A、 B、 C、 D、
-
10、用反证法证明:“在中,对边分别是a、b . 若 , 则 . ”第一步应假设( )A、 B、 C、 D、
-
11、某校九年级进行了三次数学模拟考试,甲、乙、丙三名同学的平均分和方差如表所示,则这三名同学中数学成绩最稳定的是( )
统计量
甲
乙
丙
93
93
93
14
18
11
A、甲 B、乙 C、丙 D、无法确定 -
12、将函数的图像向右平移3个单位,所得的二次函数解析式是( )A、 B、 C、 D、
-
13、二次根式中字母的取值范围是( )A、 B、 C、 D、
-
14、下列标志中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
15、正方形中,点E为上一动点(不与端点重合),连接 , 过点B作于点F,过点D作于点G.
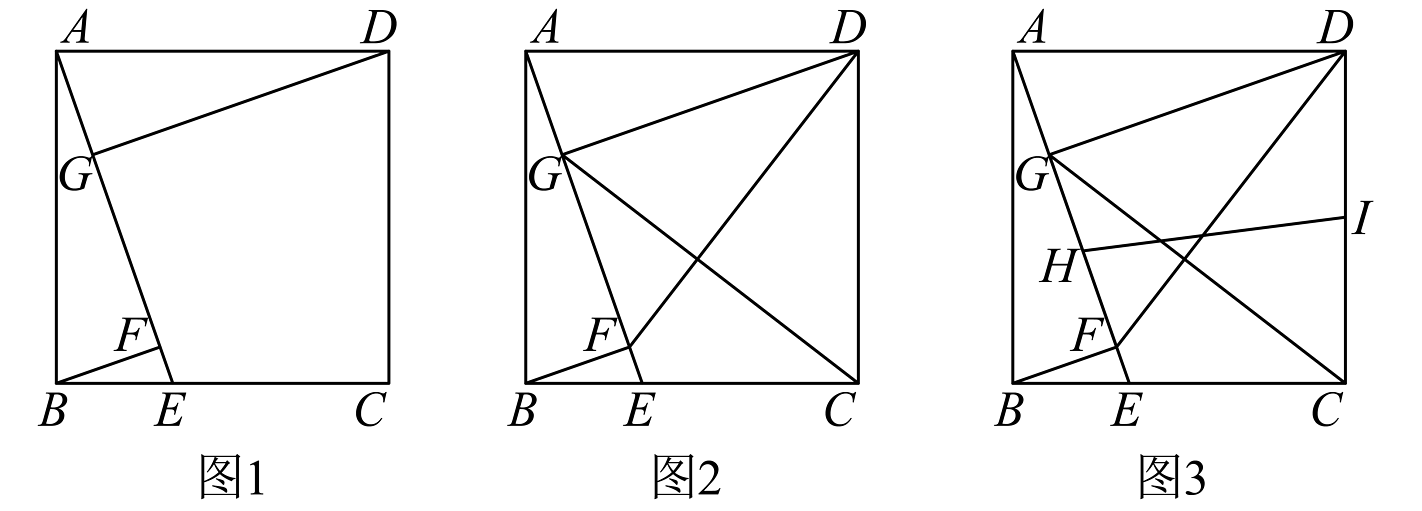 (1)、如图1,若 , , 求的长度;(2)、如图2,连结 , , 判断和的数量关系,并说明理由;(3)、如图3,点H,I分别为 , 中点,连接;判断和的数量关系,并说明理由.
(1)、如图1,若 , , 求的长度;(2)、如图2,连结 , , 判断和的数量关系,并说明理由;(3)、如图3,点H,I分别为 , 中点,连接;判断和的数量关系,并说明理由. -
16、2025年初,中国神话电影《哪吒2之魔童闹海》风靡全球,于是某书店开始销售《哪吒2》绘本.已知现在每套售价定为30元时,平均每天可售出60套;根据以往同类绘本销售规律:在每套涨价小于10元时,如果每套书每涨价1元,那么少售出4套/天;在每套降价小于10元时,如果每套书每降价1元,那么多售出1套/天.(1)、若该书店计划每套书涨价5元,根据以往同类绘本销售规律估计每天获得总销售额是多少;(2)、能否通过每套书降价x元(x为整数,),根据以往同类绘本销售规律估计,使每天获得的总销售额刚好与题(1)中的总销售额相等?若能,求出x的值;若不能,请说明理由;(3)、根据以往同类绘本销售规律书店设计了两种销售方案:
书店方案一:每套书涨价m元(m为整数,);
书店方案二:每套书降价n元(n为整数,).
是否存在这样的m,n数值,使得两种方案总销售额相等?若存在,求的比值;若不存在,请说明理由.
-
17、如图1,在中,点E,F分别在 , 上,满足 .
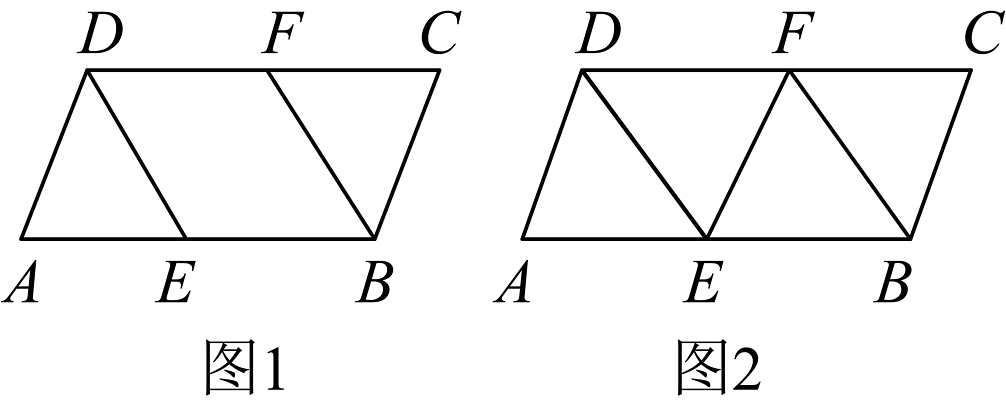 (1)、求证:四边形是平行四边形;(2)、如图2,连接 , 若 , , , 求的长.
(1)、求证:四边形是平行四边形;(2)、如图2,连接 , 若 , , , 求的长. -
18、如图,已知反比例函数的图象与正比例函数的图象交于点和点B.
 (1)、求反比例函数的表达式;(2)、点 , 判断直线与反比例函数图象除点B以外是否还有其他不同的交点,并说明理由.
(1)、求反比例函数的表达式;(2)、点 , 判断直线与反比例函数图象除点B以外是否还有其他不同的交点,并说明理由. -
19、如图,在正方形网格中,每个小正方形顶点称为格点,例如线段的端点在格点上,已知每个小正方形边长均为 , 利用无刻度直尺作图 , 请完成下列各小题.
 (1)、在图①中,以为边作一个菱形(不是正方形),其中点为格点;(2)、在图②中,以为边作正方形 , 其中点为格点.
(1)、在图①中,以为边作一个菱形(不是正方形),其中点为格点;(2)、在图②中,以为边作正方形 , 其中点为格点. -
20、为了提升学生身体素质,某小学开展“跳绳打卡”活动.某班级体育老师分别对甲乙两名同学进行了8次一分钟跳绳测试,测试结果数据如下表1,并根据测试数据绘制数据分析表如下表2.
表1 甲乙两名同学一分钟跳绳个数统计表
甲
185
165
160
185
175
180
165
185
乙
175
180
173
172
180
180
165
175
表2 测试数据分析表
平均数
中位数
众数
方差
甲
175
a
185
乙
b
175
c
(1)、根据表中的信息答下列问题:表中______; ______; ______;(2)、如果从甲乙中选择一位,代表班级参加学校组织的校跳绳比赛,您作为同班级的一份子,您会建议谁参赛较好,请说明理由.