-
1、在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是.
-
2、某老年健康活动中心随机抽取了6位老年人的收缩压数据,分别为120,96,153,146,112,136,则这组数据的40%分位数为.
-
3、如图,已知直线 , 点A是 , 之间的一个定点,点A到 , 的距离分别为1,2.点B是直线上一个动点,过点A作 , 交直线l_1于点C, , 则( )
 A、 B、面积的最小值是 C、 D、存在最小值
A、 B、面积的最小值是 C、 D、存在最小值 -
4、过所在平面外一点P,作 , 垂足为O,连接PA、PB、PC,则下列说法正确的是( )A、若 , 则点O是的外心 B、若 , , 则点O是AB边的中点 C、若 , , , 垂足都为P,则点O是的垂心 D、若P到三条边的距离相等,则点O是的重心
-
5、已知函数的定义域为R, , 则( ).A、 B、 C、是偶函数 D、是奇函数
-
6、在空间中,过点A作平面的垂线,垂足为B,记.设 , 是两个不同的平面,对空间任意一点P, , , 恒有 , 则( )A、平面\alpha与平面\beta垂直 B、平面与平面所成的(锐)二面角为 C、平面与平面平行 D、平面与平面所成的(锐)二面角为
-
7、有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球,甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7’,则( )A、甲与丙相互独立 B、甲与丁相互独立 C、乙与丙相互独立 D、丙与丁相互独立
-
8、函数在区间[-2.8,2.8]的图象大致为( )A、
 B、
B、 C、
C、 D、
D、
-
9、已知某4个数据的平均数为6,方差为3,现又加入一个数据6,此时这5个数据的方差为( )A、 B、 C、 D、
-
10、设 , , , 则a,b,c的大小关系为( )A、 B、 C、 D、
-
11、设 , 是向量,则“”是“或”的( ).A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
12、如图1,已知正方形的边长为 , 点是正方形内一动点,且 , 连结、、 , 并延长交于 .
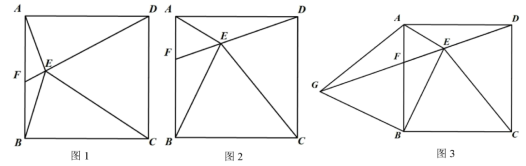 (1)、求证:;(2)、若时,
(1)、求证:;(2)、若时,①如图2,求的长度;
②如图3,延长至点 , 使得 , 连结 . 求与四边形的面积比;
(3)、在图1中,在运动过程中,当的值最小时,求的长.(直接写出答案) -
13、已知抛物线( , 为常数)经过点 , .(1)、求抛物线的函数表达式;(2)、当时, , 当时, , 且 , 为两个连续偶数,求的值;(3)、该抛物线与直线(为常数且)相交于 , 两点,且在的左侧.若在范围内,的取值恰好有3个整数值,求的取值范围.
-
14、如图,学校为美化环境,准备用总长为的篱笆,在靠墙的一侧设计一块矩形花圃 , 其中墙长 , 花圃三边外围用篱笆围起,并在边上留一个宽的门(建在处,另用其他材料).
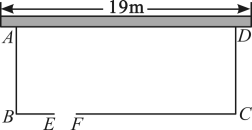 (1)、若花圃的面积为 , 求花圃的一边的长;(2)、花圃的面积能达到吗?如果能,请你给出设计方案,如果不能,请说明理由.
(1)、若花圃的面积为 , 求花圃的一边的长;(2)、花圃的面积能达到吗?如果能,请你给出设计方案,如果不能,请说明理由. -
15、如图,一次函数与反比例函数的图像交于点 , .
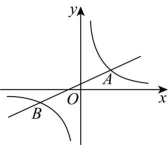 (1)、求的值和一次函数的表达式;(2)、根据函数图象,直接写出不等式的解集.
(1)、求的值和一次函数的表达式;(2)、根据函数图象,直接写出不等式的解集. -
16、2024年5月28日,神舟十八号航天员叶光富、李聪、李广苏密切协同,完成出舱活动,活动时长约 , 刷新了中国航天员单次出舱活动时间纪录,进一步激发了青少年热爱科学的热情.某校为了普及“航空航天”知识,从该校1200名学生中随机抽取了部分学生参加“航空航天”知识测试,并将测试成绩(百分制)整理绘制成如下不完整的统计图表:
成绩统计表
组别
成绩/分
百分比
A组
B组
C组
D组
E组
成绩条形统计图

根据所给信息,解答下列问题:
(1)、本次调查的成绩统计表中 , 并补全条形统计图;(2)、被抽取的学生成绩的中位数落在组(填A , B , C , D或E);(3)、试估计该校1200名学生中成绩在80分以上(包括80分)的人数. -
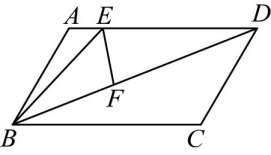
17、如图,在四边形中,是的中点,、交于点 , , .
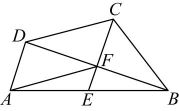 (1)、求证:四边形为平行四边形;(2)、若 , , , 求的长.
(1)、求证:四边形为平行四边形;(2)、若 , , , 求的长. -
18、解方程:(1)、(2)、
-
19、计算:
-
20、如图,在中, , , , 点、分别在线段、上,且 , 连结 , 若平分 , 则的长为 .