-
1、估计下列各数的大小：
(结果精确到0.1)； (结果精确到1).
-
2、 求下列各式的值：
-
3、两个正数的和是12，求它们积的最大值.(1)、你有哪些解决问题的方法?(2)、解决这个问题的过程中你积累了哪些经验?(3)、你还能提出哪些类似的问题?与同伴进行交流.
-
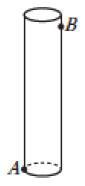
4、解决下列几个问题，并说明它们与本节课问题的区别与联系.(1)、如图，圆柱的高为13cm，底面周长为10cm，在圆柱下底面的点A处有一只蚂蚁，它想吃到离上底面1cm的点B处的食物，那么它沿圆柱侧面爬行的最短路程是多少?
(2)、如图， 一个长方体形盒子的长、宽、高分别为8cm， 8cm，12cm，一只蚂蚁想从盒底的点 A 处沿盒的外表面爬到盒顶的点 B处，你能帮蚂蚁设计一条最短的路线吗?蚂蚁爬行的最短路程是多少?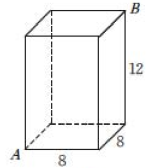
(3)、为了营造节日气氛，学校准备在大厅圆柱上缠绕彩带.已知大厅圆柱的高为6m，底面周长为2m.如果希望彩带从圆柱底端绕圆柱4圈后正好到达顶端，那么至少需要彩带多少米? -
5、如图，一个圆柱的高为12cm，底面圆的周长为18cm.在圆柱下底面的点A 处有一只蚂蚁，它想吃到上底面上与点A 相对的点B处的食物，那么它沿圆柱侧面爬行的最短路程是多少?
-
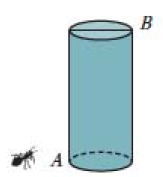
6、查阅资料，进一步了解数学史上无理数的发现历程.
-
7、请你在方格纸上按照如下要求设计直角三角形：(1)、使它的三边中恰有一边边长不是有理数；(2)、使它的三边中恰有两边边长不是有理数；(3)、使它的三边边长都不是有理数.
-
8、下图是由16个边长为1的小正方形拼成的，任意连接这些小正方形的若干顶点，可得到一些线段.试分别找出两条长度是有理数的线段和两条长度不是有理数的线段.
-
9、同一个正方形的边长和对角线的长度可能都是整数吗?
-
10、举出三个有关无理数的实例.
-
11、判断正误：(1)、所有无限小数都是无理数； ( )(2)、所有无理数都是无限小数； ( )(3)、有理数都是有限小数； ( )(4)、不是有限小数的数不是有理数. ( )
-
12、下列各数中，哪些是有理数，哪些是无理数?
- ， 3.9 ， -234.10101010…(相邻两个1之间有1个0)，0.12345678910111213…(小数部分由相继的正整数组成).
-
13、 a是一个实数，它的相反数和绝对值如何表示?若 则它的倒数如何表示?
-
14、 比较-3.14与-π的大小.
-
15、下列各数中，哪些是有理数，哪些是无理数?
0.4583， 3. ， - π，- ， 18.
-
16、下列各数中，哪些是有理数，哪些是无理数?
3.14，- ， 0. ， 0.1010001000001…(相邻两个1之间0的个数逐次加2).
-
17、如图，等边三角形ABC的边长为2，高为h，h可能是有理数吗?
-
18、归纳是数学发现的重要方法，但仅仅由几种特殊情况归纳出来的结论并不可靠.请你查阅资料，了解数学史上有关这方面的一些事例，并在班级内分享.
-
19、 如图，AB∥DE，BC∥EF， 你能判断∠ABC与的大小关系吗?小颖据此得出结论：如果两个角的两边分别平行，那么这两个角相等.你认为她的判断正确吗?
-
20、观察下列各式：
.
你能否得到结论“所有奇数都可以表示为两个自然数的平方差”?所有偶数呢?请说明理由.