2018年北师大版中考数学模拟试卷(三)
试卷更新日期:2018-05-31 类型:中考模拟
一、单选题
-
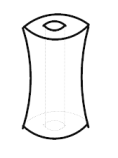
1. 下列各式不正确的是( )A、|﹣2|=2 B、﹣2=﹣|﹣2| C、﹣(﹣2)=|﹣2| D、﹣|2|=|﹣2|2. 有一实物如左下图,那么它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 2017上半年,四川货物贸易进出口总值为2 098.7亿元,较去年同期增长59.5%,远高于同期全国19.6%的整体进出口增幅.在“一带一路”倡议下,四川同期对以色列、埃及、罗马尼亚、伊拉克进出口均实现数倍增长.将2098.7亿元用科学记数法表示是( )A、 2.098 7×103 B、2.098 7×1010 C、2.098 7×1011 D、2.098 7×10124. 下列学生剪纸作品中,既是轴对称图形又是中心对称图形的是( )A、
3. 2017上半年,四川货物贸易进出口总值为2 098.7亿元,较去年同期增长59.5%,远高于同期全国19.6%的整体进出口增幅.在“一带一路”倡议下,四川同期对以色列、埃及、罗马尼亚、伊拉克进出口均实现数倍增长.将2098.7亿元用科学记数法表示是( )A、 2.098 7×103 B、2.098 7×1010 C、2.098 7×1011 D、2.098 7×10124. 下列学生剪纸作品中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列图形中,已知∠1=∠2,则可得到AB∥CD的是( )
5. 下列图形中,已知∠1=∠2,则可得到AB∥CD的是( )
A、 B、
B、 C、
C、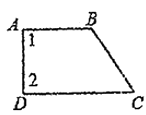 D、
D、 6. 不等式组 的解集是( )
6. 不等式组 的解集是( )
A、无解 B、 C、x ≥ D、-1<x ≤7. 在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C=( )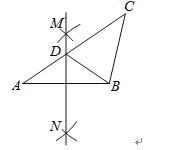 A、40° B、50° C、60° D、70°8. 下列说法正确的是( )
A、40° B、50° C、60° D、70°8. 下列说法正确的是( )①面积之比为1:2的两个相似三角形的周长之比是1:4;②三视图相同的几何体是正方体;③﹣27没有立方根;④对角线互相垂直的四边形是菱形;⑤某中学人数相等的甲、乙两班学生参加了同一次数学测验,班平均分和方差分别为 =82分, =82分,S2甲=245,S2乙=190,那么成绩较为整齐的是乙班.
A、1个 B、2个 C、3个 D、4个9. 已知A样本的数据如下:72,73,76,76,77,78,78,78,B样本的数据恰好是A样本数据每个都加2,则A,B两个样本的下列统计量对应相同的是( )
A、平均数 B、方差 C、中位数 D、众数10. 济南大明湖畔的“超然楼”被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量,如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60m至B处,测得仰角为60°,若学生的身高忽略不计, ≈1.7,结果精确到1m,则该楼的高度CD为( )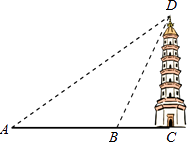 A、47m B、51m C、53m D、54m11.
A、47m B、51m C、53m D、54m11.如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( )
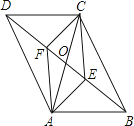 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
12. 多项式x(x﹣1)﹣3x+4因式分解的结果等于 .13. 一个不透明盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是 .14. 请看杨辉三角(1),并观察下列等式(2):根据前面各式的规律,则(a+b)6的第三项的系数为 .
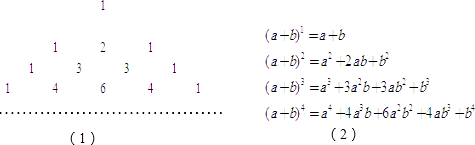 15. 如图,已知∠A=ɑ,∠ACD 是△ABC 的外角,∠ABC 的平分线与∠ACD 的平分线相交于点 A1 , 得∠A1;若∠A1BC 的 平分线与∠A1CD 的平分线相交于点 A2 , 得∠A2…∠A2015BC 的平分线与∠A2015CD 的平分线相交于点 A2016 , 得∠A2016 , 则∠A2016= . (用含ɑ的式子表示)
15. 如图,已知∠A=ɑ,∠ACD 是△ABC 的外角,∠ABC 的平分线与∠ACD 的平分线相交于点 A1 , 得∠A1;若∠A1BC 的 平分线与∠A1CD 的平分线相交于点 A2 , 得∠A2…∠A2015BC 的平分线与∠A2015CD 的平分线相交于点 A2016 , 得∠A2016 , 则∠A2016= . (用含ɑ的式子表示)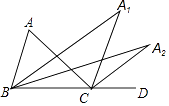
三、综合题
-
16. 计算: .17. 先化简再求值:( +1)÷ ,其中a=2+ .18. 网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
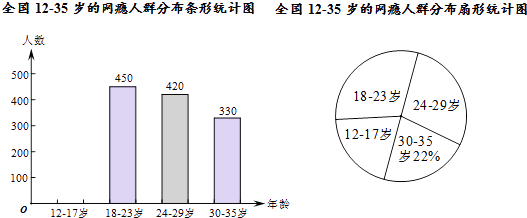
请根据图中的信息,回答下列问题:
(1)、这次抽样调查中共调查了人;(2)、请补全条形统计图;(3)、扇形统计图中18﹣23岁部分的圆心角的度数是;(4)、据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数.19. 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是多少?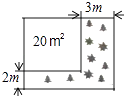 20.
20.如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,m)在边AB上,反比例函数y= (k≠0)在第一象限内的图象经过点D、E,且cos∠BOA= .
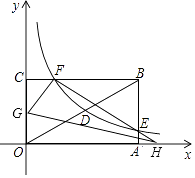 (1)、求边AB的长;(2)、求反比例函数的解析式和m的值;(3)、若反比例函数的图象与矩形的边BC交于点F,点G、H分别是y轴、x轴上的点,当△OGH≌△FGH时,求线段OG的长.21. 如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,
(1)、求边AB的长;(2)、求反比例函数的解析式和m的值;(3)、若反比例函数的图象与矩形的边BC交于点F,点G、H分别是y轴、x轴上的点,当△OGH≌△FGH时,求线段OG的长.21. 如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D, (1)、若PD∥BC,求证:AP平分∠CAB;(2)、若PB=BD,求PD的长度;(3)、证明:无论点P在 上的位置如何变化,CP•CQ为定值.22. 已知二次函数y=ax2+bx-2的图象与x轴交于A,B两点,与y轴交于点C,点A的坐标为(4,0),且当x=-2和x=5时二次函数的函数值y相等.
(1)、若PD∥BC,求证:AP平分∠CAB;(2)、若PB=BD,求PD的长度;(3)、证明:无论点P在 上的位置如何变化,CP•CQ为定值.22. 已知二次函数y=ax2+bx-2的图象与x轴交于A,B两点,与y轴交于点C,点A的坐标为(4,0),且当x=-2和x=5时二次函数的函数值y相等. (1)、求实数a,b的值;
(1)、求实数a,b的值;
(2)、如图①,动点E,F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒 个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由;
②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式.