2018年北师大版中考数学模拟试卷（一）

试卷更新日期：2018-05-31 类型：中考模拟

进入出卷网下载

一、选择题

1. 小胖同学买了3袋标注质量为200克的食品，他对这3袋食品的实际质量进行了检测，检测结果（用正数记超过标注质量的克数，用负数记不足标注质量的克数）如下：+10、﹣16、﹣11，则这3袋食品的实际质量为（）

A、600克 B、593克 C、603克 D、583克

查看试题解析
2.
图（1）是一个小正方体的表面展开图，小正方体从图（2）所示的位置依次翻到第1格、第2格、第3格、第4格，这时小正方体朝上一面的字是（　　）

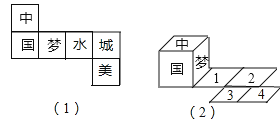A、梦 B、水 C、城 D、美

查看试题解析
3. 下列各组的两个数中，运算后结果相等的是（）

A、2³和3² B、﹣5³和（﹣5）³ C、﹣|﹣5|和﹣（﹣5） D、（﹣ $\frac{2}{3}$ ）³和﹣ $\frac{2^{3}}{3}$

查看试题解析
4. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 保护水资源，人人有责．我国是缺水国家，目前可利用淡水资源总量仅约为899000亿m³ ，数据899000用科学记数法表示为（）

A、8.99×10⁵ B、0.899×10⁶ C、8.99×10⁴ D、89.9×10⁴

查看试题解析
6. 如图1，直线AB∥CD，∠A＝70°，∠C＝40°，则∠E等于（）

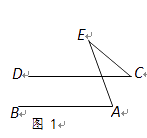A、30° B、40° C、60° D、70°

查看试题解析
7. 某校举行以“激情五月，唱响青春”为主题的演讲比赛．决赛阶段只剩下甲、乙、丙、丁四名同学，则甲、乙同学获得前两名的概率是（ )

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
8. 下列四个命题中，真命题有（）
①两条直线被第三条直线所截，内错角相等．
②如果∠1和∠2是对顶角，那么∠1=∠2．
③三角形的一个外角大于任何一个内角．
④如果x²＞0，那么x＞0．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 甲车行驶30千米与乙车行驶40千米所用时间相同，已知乙车每小时比甲车多行驶15千米，设甲车的速度为x千米/小时，依据题意列方程正确的是（）

A、 $\frac{30}{x} = \frac{40}{x - 15}$ B、 $\frac{30}{x - 15} = \frac{40}{x}$ C、 $\frac{30}{x} = \frac{40}{x + 15}$ D、 $\frac{30}{x + 15} = \frac{40}{x}$

查看试题解析
10. 若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式，如a+b+c就是完全对称式．下列三个代数式：
①（a-b）²；②ab+bc+ca；③a²b+b²c+c²a．其中是完全对称式的是（　　）

A、①② B、①③　 C、②③ D、①②③

查看试题解析
11. 如图，在边长为6的菱形ABCD中，∠DAB=60°，以点D为圆心，菱形的高DF为半径画弧，交AD于点E，交CD于点G，则图中阴影部分的面积是（）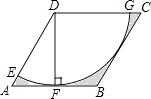

A、18 $\sqrt{3}$ ﹣9π B、18﹣3π C、9 $\sqrt{3}$ ﹣ $\frac{9 π}{2}$ D、18 $\sqrt{3}$ ﹣3π

查看试题解析
12. 在正方形ABCD中，点E为BC边的中点，点与点B关于AE对称，与AE交于点F，连接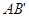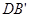，，FC。下列结论：① 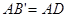；② 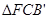为等腰直角三角形；③ 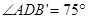；④ 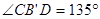。其中正确的是( ）

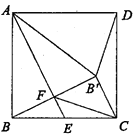A、①② B、①②④ C、③④ D、①②③④

查看试题解析

二、填空题

13. 分解因式：2xy²+4xy+2x= ．

查看试题解析
14. 已知一组数据a₁ ， a₂ ， a₃ ， a₄的平均数是2017，则另一组数据a₁+3，a₂﹣2，a₃﹣2，a₄+5的平均数是．

查看试题解析
15. 如图，菱形ABCD中，∠DAB=60°，DF⊥AB于点E，且DF=DC，连结PC，则∠DCF的度数为度．

查看试题解析
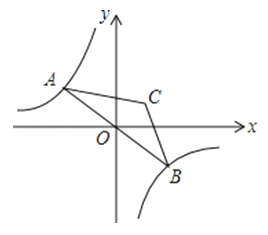
16.
如图，点A是双曲线y=﹣ $\frac{9}{x}$ 在第二象限分支上的一个动点，连接AO并延长交另一分支于点B，以AB为底作等腰△ABC，且∠ACB=120°，点C在第一象限，随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y= $\frac{k}{x}$ 上运动，则k的值为．

查看试题解析

三、解答题

17. 计算： $\sin 30 ° \times \cos 45 ° - \tan 60 ° + | 1 - \sqrt{3} |$ |．

查看试题解析
18. 求不等式组 ${\begin{matrix} 3 x + 3 > 5 (x - 1) ① \\ \frac{2 x - 2}{3} - 1 \leq \frac{3 x}{2} ② \end{matrix}$ 的解集，并把它们的解集在数轴上表示出来．

查看试题解析
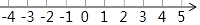19.
某市为提高学生参与体育活动的积极性，2016年9月围绕“你最喜欢的体育运动项目（只写一项）”这一问题，对初一新生进行随机抽样调查，下图是根据调查结果绘制成的统计图（不完整）．
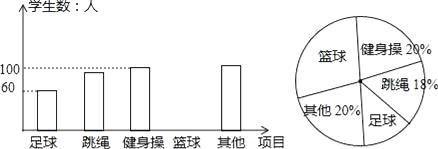
请你根据图中提供的信息解答下列问题：

(1)、本次抽样调查的样本容量是多少？

(2)、根据条形统计图中的数据，求扇形统计图中“最喜欢足球运动”的学生数所对应扇形的圆心角度数．

(3)、请将条形统计图补充完整．

(4)、若该市2016年约有初一新生18000人，请你估计全市本届学生中“最喜欢足球运动”的学生约有多少人．

查看试题解析
20. “C919”大型客机首飞成功，激发了同学们对航空科技的兴趣，如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸，图中AB∥CD，AM∥BN∥ED，AE⊥DE，请根据图中数据，求出线段BE和CD的长．（sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，结果保留小数点后一位）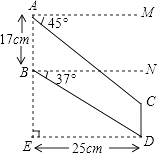

查看试题解析
21. 为迎接“国家卫生城市”复检，某市环卫局准备购买A、B两种型号的垃圾箱，通过市场调研得知：购买3个A型垃圾箱和2个B型垃圾箱共需540元；购买2个A型垃圾箱比购买3个B型垃圾箱少用160元．

(1)、每个A型垃圾箱和B型垃圾箱各多少元？

(2)、现需要购买A，B两种型号的垃圾箱共300个，分别由甲、乙两人进行安装，要求在12天内完成（两人同时进行安装）．已知甲负责A型垃圾箱的安装，每天可以安装15个，乙负责B型垃圾箱的安装，每天可以安装20个，生产厂家表示若购买A型垃圾箱不少于150个时，该型号的产品可以打九折；若购买B型垃圾箱超过150个时，该型号的产品可以打八折，若既能在规定时间内完成任务，费用又最低，应购买A型和B型垃圾箱各多少个？最低费用是多少元？

查看试题解析
22. 如图，⊙O是△ABC的外接圆，BC是⊙O的直径，∠ABC=30°，过点B作⊙O的切线BD与CA的延长线交于点D，与半径AO的延长线交于点E，过点A作⊙O的切线AF，与直径BC延长线交于点F.

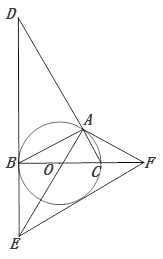(1)、求证：△ACF∽△DAE；

(2)、若S ∆AOC= $\frac{\sqrt{3}}{4}$ ，求DE的长；

(3)、连接EF，求证：EF是⊙O的切线.

查看试题解析
23. 如图，抛物线y=﹣x²+bx+c与x轴交于点A（﹣1，0），B（5，0）两点，直线 $y = - \frac{3}{4} x + 3$ 与y轴交于点C，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．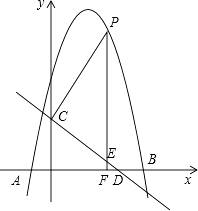

(1)、求抛物线的解析式；

(2)、若PE=5EF，求m的值；

(3)、若点E′ 是点E关于直线PC的对称点（E与C不重合），是否存在点P，使点E′ 落在y轴上？若存在，请求出相应的点P的坐标；若不存在，请说明理由．

查看试题解析