2015-2016学年广东省深圳市南山区九年级上学期期末数学试卷

试卷更新日期：2016-12-30 类型：期末考试

进入出卷网下载

一、选择题

1. 如图的几何体是由五个同样大小的正方体搭成的，其主视图是（）

A、 B、 C、 D、

查看试题解析
2. 一元二次方程x²﹣9=0的解是（　　）

A、x=﹣3 B、x=3 C、x₁=3，x₂=﹣3 D、x=81

查看试题解析
3. 点（2，﹣2）是反比例函数y= $\frac{k}{x}$ 的图象上的一点，则k=（）

A、﹣1 B、 $\frac{1}{4}$ C、﹣4 D、﹣ $\frac{1}{4}$

查看试题解析
4. 下列关于x的一元二次方程有实数根的是（）

A、x²+1=0 B、x²+x+1=0 C、x²﹣x+1=0 D、x²﹣x﹣1=0

查看试题解析
5. 一个口袋中有2个红球，3个白球，这些球除色外都相同，从口袋中随机摸出一个球，这个球是红球的概率是（）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{1}{5}$ D、 $\frac{1}{2}$

查看试题解析
6. 顺次连结对角线相等的四边形的四边中点所得图形是（）

A、正方形 B、矩形 C、菱形 D、以上都不对

查看试题解析
7. 如图，在菱形ABCD中，BD=6，AC=8，则菱形ABCD的周长为（）

A、20 B、16 C、25 D、30

查看试题解析
8. 下列命题中，假命题的是（）

A、四边形的外角和等于内角和 B、对角线互相垂直的平行四边形是菱形 C、矩形的四个角都是直角 D、相似三角形的周长比等于相似比的平方

查看试题解析
9. 如图，平行于BC的直线DE把△ABC分成的两部分面积相等，则 $\frac{D E}{B C}$ =（）

A、 $\frac{1}{4}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
10. 已知 $\frac{a}{b}$ = $\frac{c}{d}$ = $\frac{e}{f}$ = $\frac{1}{3}$ （b+d+f≠0），则 $\frac{a + c + e}{b + d + f}$ =（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
11. 下列命题中，
①有一组邻边互相垂直的菱形是正方形
②若2x=3y，则 $\frac{x}{y}$ = $\frac{2}{3}$
③若（﹣1，a）、（2，b）是双曲线y= $\frac{2}{x}$ 上的两点，则a＞b
正确的有（）个．

A、1 B、2 C、3 D、0

查看试题解析
12. 如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（）

A、2 B、 $\sqrt{3}$ C、 $2 \sqrt{2}$ D、 $2 \sqrt{3}$

查看试题解析

二、填空题

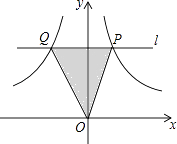
13. 若x=﹣2是关于x的一元二次方程x²+3x+m+1=0的一个解，则m= ．

查看试题解析
14. 一个暗箱里放有a个除颜色外完全相同的球，这a个球中红球只有3个．若每次将球搅匀后，任意摸出1个球记下颜色再放回暗箱．通过大量重复摸球试验后发现，摸到红球的频率稳定在20%附近，那么可以推算出a的值大约是

查看试题解析
15. 如图，在平面直角坐标系中，直线l∥x轴，且直线l分别与反比例函数y= $\frac{6}{x}$ （x＞0）和y=﹣ $\frac{8}{x}$ （x＜0）的图象交于点P，Q，连结PO、QO，则△POQ的面积为
+

查看试题解析
16. 如图，已知正方形ABCD的边长为4，点E、F分别在边AB，BC上，且AE=BF=1，则OC=

查看试题解析

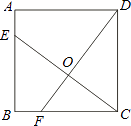
三、解答题

17. 解方程：x²+6x﹣7=0．

查看试题解析
18. 一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．

(1)、若从中任取一个球，求摸出球上的汉字刚好是“美”的概率；

(2)、甲从中任取一球，不放回，再从中任取一球，请用树状图或列表法，求甲取出的两个球上的汉字恰能组成“美丽”或“南山”的概率．

查看试题解析
19. 如图，阳光下，小亮的身高如图中线段AB所示，他在地面上的影子如图中线段BC所示，线段DE表示旗杆的高，线段FG表示一堵高墙．

(1)、请你在图中画出旗杆在同一时刻阳光照射下形成的影子；

(2)、如果小亮的身高AB=1.6m，他的影子BC=2.4m，旗杆的高DE=15m，旗杆与高墙的距离EG=16m，请求出旗杆的影子落在墙上的长度．

查看试题解析
20. 如图，已知菱形ABCD中，对角线AC、BD相交于点O，过点C作CE∥BD，过点D作DE∥AC，CE与DE相交于点E．

(1)、求证：四边形CODE是矩形；

(2)、若AB=5，AC=6，求四边形CODE的周长．

查看试题解析
21. 贵阳市某楼盘准备以每平方米6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米4860元的均价开盘销售．

(1)、求平均每次下调的百分率．

(2)、某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：
①打9.8折销售；
②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？

查看试题解析
22. 如图，Rt△ABO的顶点A是双曲线y₁= $\frac{k}{x}$ 与直线y₂=﹣x﹣（k+1）在第二象限的交点．AB⊥x轴于B，且S_△_ABO= $\frac{3}{2}$ ．

(1)、求这两个函数的解析式；

(2)、求△AOC的面积；

(3)、直接写出使y₁＞y₂成立的x的取值范围．

查看试题解析
23.
如图，在平面直角坐标系中，四边形ABCD是平行四边形，AD=6，若OA、OB的长是关于x的一元二次方程x²﹣7x+12=0的两个根，且OA＞OB．

(1)、求OA、OB的长．

(2)、若点E为x轴正半轴上的点，且S_△_AOE= $\frac{16}{3}$ ，求经过D、E两点的直线解析式及经过点D的反比例函数的解析式，并判断△AOE与△AOD是否相似．

(3)、若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，直接写出F点的坐标，若不存在，请说明理由．

查看试题解析