2015-2016学年广东省深圳市龙华新区九年级上学期期末数学试卷

试卷更新日期：2016-12-30 类型：期末考试

进入出卷网下载

一、选择题

1. 方程x²=x的解是（）

A、1 B、0 C、1和﹣1 D、0和1

查看试题解析
2. 如图是一种常用的圆顶螺杆，它的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 已知点A（1，2）、B（﹣1，b）是反比例函数y= $\frac{k}{x}$ 图象上的一点，则b的值为（）

A、﹣2 B、2 C、﹣ $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
4. 如图，已知l₁∥l₂∥l₃ ，直线AC分别交l₁、l₂、l₃于点A，B，C，直线DF分别交l₁、l₂、l₃于D，E，F，DE=4，EF=6，AB=5，则BC的长为（）

A、 $\frac{25}{2}$ B、 $\frac{15}{2}$ C、 $\frac{25}{3}$ D、 $\frac{10}{3}$

查看试题解析
5. 一个口袋中有红球、黄球共20个，这些除颜色外都相同，将口袋中的球搅拌均匀，从中随机摸出一球，记下颜色后再放回口袋，不断重复这一过程，共摸了200次，发现其中有161次摸到红球．则这个口袋中红球数大约有（　　）

A、4个 B、10个 C、16个 D、20个

查看试题解析
6. 如图，△ABC中，D为AB的中点，DE∥BC，则下列结论中错误的是（）

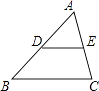A、 $\frac{A D}{B D} = \frac{D E}{B C}$ B、 $\frac{A D}{B D} = \frac{A E}{E C}$ C、DE= $\frac{1}{2}$ BC D、S_△_ADE= $\frac{1}{3}$ S_四边形_BCED

查看试题解析
7. 将二次函数y=x²﹣4的图象先向右平移2个单位，再向上平移3个单位后得到的抛物线的函数表达式为（）

A、y=（x+2）²﹣7 B、y=（x﹣2）²﹣7 C、y=（x+2）²﹣1 D、y=（x﹣2）²﹣1

查看试题解析
8. 如图，矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD于E，若∠OAE=24°，则∠BAE的度数是（）

A、24° B、33° C、42° D、43°

查看试题解析
9. 如图，某数学学习兴趣小组为了测量树AB的度数，他们测得此树在阳光下的影子BC的长为9m，在相同时刻，他们还测得小亮在阳光下的影长为1.5m，已知小亮的身高为1.8m，则树AB的高为（）

A、10.8m B、9m C、7.5m D、0.3m

查看试题解析
10. 下列命题中，是真命题的是（）

A、对角线互相垂直的平行四边形是正方形 B、相似三角形的周长之比等于相似的平方 C、若（1，y₁）、（2，y₂）是双曲线y=﹣ $\frac{1}{x}$ 上的两点，则y₁＜y₂ D、方程x²﹣2x+3=0有两个不相等的实数根

查看试题解析
11. 如图，已知正方形ABCD的边长为4，E是BC的中点，过点E作EF⊥AE，交CD于点F，连接AF并延长，交BC的延长线于点G．则CG的长为（）

A、 $\frac{3}{4}$ B、1 C、 $\frac{4}{3}$ D、2

查看试题解析
12. 已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，有如下结论：
①a＞0；②b＞0；③a+b+c＞0；④2a+b=0；⑤方程ax²+bx+c=0的解为x₁=﹣1，x₂=3．
其中正确的是（）

A、①②③ B、②③④ C、③④⑤ D、①④⑤

查看试题解析

二、填空题

13. 已知3a=4b，那么 $\frac{a}{b}$ = ．

查看试题解析
14. 某路基的横截面如图所示，路基高BC=1m，斜坡AB的坡度为1：2，则斜坡AB的长为 m．

查看试题解析
15. 如图，已知A是双曲线y= $\frac{2}{x}$ （x＞0）上一点，过点A作AB∥y轴，交双曲线y=﹣ $\frac{1}{x}$ （x＞0）于点B，过点B作BC⊥AB交y轴于点C，连接AC，则△ABC的面积为．

查看试题解析
16. 如图，已知矩形ABCD中，AB=4，E是BC上一点，将△CDE沿直线DE折叠后，点C落在点C′处，连接C′E交AD于点F，若BE=2，F为AD的中点，则AD的长为．

查看试题解析

三、解答题

17. 计算：2sin²45°﹣tan60°•cos30°．

查看试题解析
18. 解方程：x²+4x﹣12=0．

查看试题解析
19. 如图是两个可以自由转动的转盘，转盘A被分成三个面积相等的扇形，转盘B被分成两个面积相等的扇形．

(1)、转动转盘A一次，所得到的数字是负数的概率为

(2)、转动两个转盘各一次，请用列表法或画树状图法求所得到的数字均是负数的概率．

查看试题解析
20. 2015年深圳国际马拉松赛于12月7日拉开帷幕，某马拉松爱好者用无人机拍摄比赛过程．如图，在无人机的镜头C下，观测深南大道A处的俯角为30°，B处的俯角为45°．如果此时无人机镜头C处离路面的高度CD为100米，点A、D、B在同一直线上，求A、B两处之间的距离．

查看试题解析
21. 某市2012年投入教育经费是180亿元，2014年投入教育经费是304.2亿元．

(1)、求2012年至2014年该市投入教育经费的年平均增长率；

(2)、根据（1）所得的年平均增长率，预计2015年该市将投入教育经费多少亿元．

查看试题解析
22.
如图，已知菱形ABCD中，AB=6，∠B=60°．E是BC边上一动点，F是CD边上一动点，且BE=CF，连接AE、AF．

(1)、∠EAF的度数是；

(2)、求证：AE=AF；

(3)、延长AF交BC的延长线于点G，连接EF，设BE=x，EF²=y，求y与x之间的函数关系式．

查看试题解析
23.
如图1，已知直线l：y=﹣x+2与x轴交于点A、与y轴交于点B．抛物线y=ax²+bx+c（a≠0）经过O、A两点，与直线l交于点C，点C的横坐标为﹣1．

(1)、求该抛物线的函数表达式；

(2)、若点P是位于直线l下方抛物线上的一个动点，且不与点A、点C重合，连接PA、PC．设△PAC的面积为S，求当S取得最大值时点P的坐标，并求S的最大值；

(3)、
如图2，设抛物线的顶点为D，连接AD、BD．点E是对称轴m上一点，F是抛物线上一点，请直接写出当△DEF与△ABD相似时点E的坐标．

查看试题解析