2015-2016学年广东省揭阳市揭西县九年级上学期期末数学试卷
试卷更新日期:2016-12-30 类型:期末考试
一、选择题
-
1. 点P(﹣2,b)是反比例函数y= 的图象上的一点,则b=( )A、﹣2 B、﹣1 C、1 D、22. 用因式分解法解一元二次方程x(x﹣3)=x﹣3时,原方程可化为( )A、(x﹣1)(x﹣3)=0 B、(x+1)(x﹣3)=0 C、x (x﹣3)=0 D、(x﹣2)(x﹣3)=03. 准备两组相同的牌,每组两张且大小相同,两张牌的牌面数字分别是0,1,从每组牌中各摸出一张牌,两张牌的牌面数字和为1的概率为( )A、 B、 C、 D、4. 关于x的一元二次方程x2+(m﹣2)x+m+1=0有两个相等的实数根,则m的值是( )A、0 B、8 C、4±2 D、0或85.
如图是同一时刻学校里一棵树和旗杆的影子,如果树高为3米,测得它的影子长为1.2米,旗杆的高度为5米,则它的影子长为( )
 A、4米 B、2米 C、1.8米 D、3.6米6. 如图,三角形ABC中,D,E,F分别是AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=1:2,BC=30cm,则FC的长为( )
A、4米 B、2米 C、1.8米 D、3.6米6. 如图,三角形ABC中,D,E,F分别是AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=1:2,BC=30cm,则FC的长为( ) A、10cm B、20cm C、5cm D、6cm7. 如图,桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,其左视图是( )
A、10cm B、20cm C、5cm D、6cm7. 如图,桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,其左视图是( )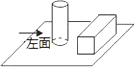 A、
A、 B、
B、 C、
C、 D、
D、 8. 已知点P(1,2)在反比例函数y= 的图象上,过P作x轴的垂线,垂足为M,则△OPM的面积为( )A、2 B、4 C、8 D、19.
8. 已知点P(1,2)在反比例函数y= 的图象上,过P作x轴的垂线,垂足为M,则△OPM的面积为( )A、2 B、4 C、8 D、19.如图,为了估计河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )
 A、40m B、60m C、120m D、180m10. 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE= AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
A、40m B、60m C、120m D、180m10. 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE= AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 方程(x﹣2)2=9的解是 .12. 反比例函数y= 经过点(﹣2,1),则一次函数y=x+k的图象经过点(﹣1,).13. 两位同学玩“石头、剪子、布”游戏,随机出手一次,两人手势相同的概率是 .
 14. 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD,垂足为E,ED=3BE,则∠AOB的度数为 .
14. 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD,垂足为E,ED=3BE,则∠AOB的度数为 . 15. 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF;EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为 .
15. 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF;EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为 . 16. 如图,正方形ABCD的边长为3,延长CB到点M,使BM=1,连接AM,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为 .
16. 如图,正方形ABCD的边长为3,延长CB到点M,使BM=1,连接AM,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为 .
三、解答题
-
17. 解一元二次方程:x2﹣x﹣6=0.18. 直线y=x+b与反比例函数y= (x>0)的图象交于点A(1,2),写出这两个函数的表达式.19. 如图,在正方形ABCD中,点E在AB上,点F在BC的延长线上,且AE=CF,求证:DE=DF.
 20. 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与x、y轴交于点A(1,0),B(0,﹣1)与反比例函数y= 在第一象限内的图象交于点C,点C的纵坐标为1.
20. 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与x、y轴交于点A(1,0),B(0,﹣1)与反比例函数y= 在第一象限内的图象交于点C,点C的纵坐标为1. (1)、求一次函数的解析式;(2)、求点C的坐标及反比例函数的解析式.21. 某班从3名男生和2名女生中随机抽出2人参加演讲比赛,求所抽取的两名学生中至少有一名女生的概率.22. 已知:如图,在矩形ABCD中,对角线AC,BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)、求一次函数的解析式;(2)、求点C的坐标及反比例函数的解析式.21. 某班从3名男生和2名女生中随机抽出2人参加演讲比赛,求所抽取的两名学生中至少有一名女生的概率.22. 已知:如图,在矩形ABCD中,对角线AC,BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证: (1)、△ODE≌△FCE;(2)、四边形ODFC是菱形.23. 某小区在绿化工程中有一块长为20m、宽为8m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为56m2 , 两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
(1)、△ODE≌△FCE;(2)、四边形ODFC是菱形.23. 某小区在绿化工程中有一块长为20m、宽为8m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为56m2 , 两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.

